High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Addition and subtraction 2D shapes Regular polygonsPerimeter
Here you will learn what perimeter is, how to find perimeter of various shapes and how to apply perimeter to real world scenarios.
Students will first learn how to find perimeter as part of their work in measurement and data in 3 rd grade and 4 th grade and expand their knowledge as they progress through middle and high school.
What is the perimeter?
The perimeter of a two-dimensional shape is the sum of the lengths of each of the sides.
Perimeter of squares
Let’s find the perimeter of the square.

The perimeter is found by summing the lengths of all the sides of the square.
Since a square has four side lengths that are the same measurement, you can add:
7+7+7+7=28
The perimeter of this square is 28 units.
Another way to find the perimeter of a square is to multiply one side length by 4 .
\begin{aligned}& P=4(7) \\\\ & P=28\end{aligned}
The perimeter is 28 units.
Step-by-step guide: Perimeter of squares
Perimeter of triangles
Let’s find the perimeter of a triangle.

The perimeter is found by summing the lengths of all the sides of the triangle.
5+12+13=20
The perimeter of the triangle is 20 units.
Find a missing side using the perimeter
You can also figure out the missing side length of a polygon when you are given the perimeter.
For example, find the missing side of the triangle.
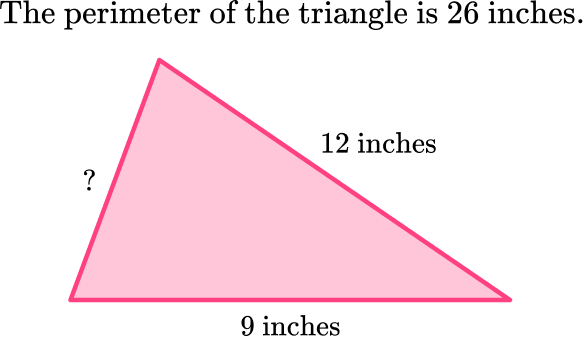
In order to find the missing side length, think about what number can be put in place of the “?” to make the equation true.
\begin{aligned}& 9+12 \; + \; ?=26 \\\\ & 21 \; + \; ?=26\end{aligned}
Replacing the “?” with 5 will make the equation true.
21+5=26
5 inches is the length of the missing side.
Step-by-step guide: Perimeter of a triangle
![[FREE] Perimeter Worksheet (Grade 3 and 4)](https://thirdspacelearning.com/wp-content/uploads/2024/06/Perimeter-Worksheet-listing-image.png)
[FREE] Perimeter Worksheet (Grade 3 and 4)
![[FREE] Perimeter Worksheet (Grade 3 and 4)](https://thirdspacelearning.com/wp-content/uploads/2024/06/Perimeter-Worksheet-listing-image.png)
Use this worksheet to check your grade 3 and 4 students’ understanding of perimeter. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Perimeter Worksheet (Grade 3 and 4)](https://thirdspacelearning.com/wp-content/uploads/2024/06/Perimeter-Worksheet-listing-image.png)
[FREE] Perimeter Worksheet (Grade 3 and 4)
![[FREE] Perimeter Worksheet (Grade 3 and 4)](https://thirdspacelearning.com/wp-content/uploads/2024/06/Perimeter-Worksheet-listing-image.png)
Use this worksheet to check your grade 3 and 4 students’ understanding of perimeter. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEPerimeter of rectangles
Let’s find the perimeter of the rectangle.

The perimeter is found by summing the lengths of all the sides of the rectangle.
8+8+3+3=22
The perimeter of the rectangle is 22 units.
You can also use a formula to find the perimeter of a rectangle.
\begin{aligned}& P=(2 \times \text { length })+(2 \times \text { width }) \\\\ & P=2 l+2 w \end{aligned}
Applying the formula to find the perimeter:

\begin{aligned}& \text { length }=8 \text { units } \\\\ & \text { width }=3 \text { units }\end{aligned}
\begin{aligned}& P=2(8)+2(3) \\\\ & P=16+6 \\\\ & P=22\end{aligned}
The perimeter is 22 units.
Find a missing dimension of a rectangle using the perimeter
Find the width of the rectangle.
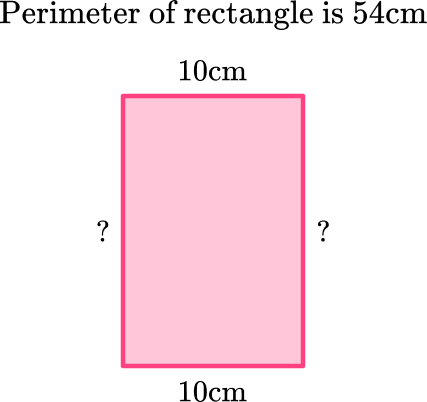
P=\text { length }+ \text { length }+ \text { width }+ \text { width }
Think about the number that makes the equation true.
\begin{aligned}& 54=10+10 \; + \; ? \; + \; ? \\\\ & 54=20 \; + \; ? \; + \; ? \\\\ & 54=20+34\end{aligned}
34 represents the sum of both sides, which means 17 is the measurement of the width because:
17+17=34
17 \, cm is the width of the rectangle.
You can also use the formula for the perimeter of a rectangle to find the width (which is a 7 th grade skill).
\begin{aligned}& P=2 l+2 w \\\\ & 54=2(10)+2 w \\\\ & 54=20+2 w \\\\ & 54-20=20-20+2 w \\\\ & 34=2 w \\\\ &\cfrac{34}{2}=\cfrac{2 w}{2} \\\\ & 17=w\end{aligned}
The width is 17 \, cm .
Step-by-step guide: Perimeter of a rectangle
What is the perimeter?

Common Core State Standards
How does this relate to 3 rd grade – 7 th grade math?
- Grade 3 – Measurement and data (3.MD.D.8)
Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.
- Grade 4 – Measurement and data (4.MD.A.3)
Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
- Grade 5 – Geometry (5.G.B.4)
Classify two-dimensional figures in a hierarchy based on properties.
- Grade 6 – Geometry (6.G.A.3)
Draw polygons in the coordinate plane given coordinates for the vertices; use coordinates to find the length of a side joining points with the same first coordinate or the same second coordinate. Apply these techniques in the context of solving real-world and mathematical problems.
- Grade 7 – Expressions and equations (7.EE.B.4a)
Solve word problems leading to equations of the form px+q=r and p \, (x + q)=r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approach. For example, the perimeter of a rectangle is 54 \, cm . Its length is 6 \, cm . What is its width?
How to find perimeter
There are several strategies to find the perimeter of 2 D shapes. For more specific step-by-step guides, check out the individual pages linked in the “What is Perimeter?” section above or read through the examples below.
In order to calculate the perimeter of a shape:
- Add all the side lengths or apply the formula.
- Write the final answer with the correct units.
Step-by-step guide: How to find perimeter
How to find perimeter examples
Example 1: equilateral triangle
What is the perimeter of the triangle?

- Add all the side lengths or apply the formula.
The length of each side is 1 \cfrac{1}{5} \mathrm{~cm}.
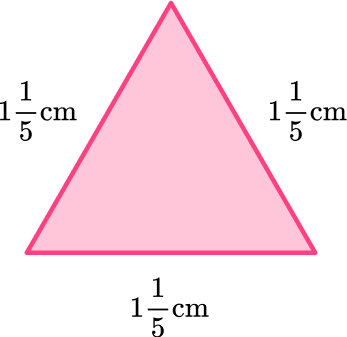
To find the perimeter, add up all the side lengths.
\begin{aligned}& P=1 \cfrac{1}{5}+1 \cfrac{1}{5}+1 \cfrac{1}{5} \\\\ & P=3 \cfrac{3}{5}\end{aligned}
OR since all the sides are the same length, you can multiply 1 \cfrac{1}{5} by 3.
\begin{aligned}& P=3 \times 1 \cfrac{1}{5} \\\\ & P=\cfrac{3}{1} \times \cfrac{6}{5} \\\\ & P=\cfrac{18}{5}=3 \cfrac{3}{5} \end{aligned}
2Write the final answer with the correct units.
The perimeter of the triangle is 3 \cfrac{3}{5} {~cm} .
Example 2: square
Find the perimeter of the square.
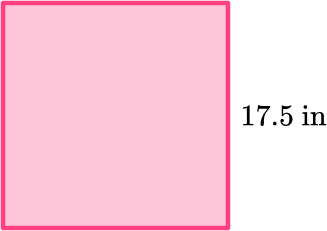
Add all the side lengths or apply the formula.
All sides of a square are congruent (equal) so each side’s length is 17.5 inches.

To find the perimeter, add up all the side lengths.
17.5+17.5+17.5+17.5=70
OR since all the side lengths are the same, you can multiply 17.5 by 4 .
4 \times 17.5=70
Write the final answer with the correct units.
The perimeter of the square is 70 inches.
Example 3: perimeter of rectangle
What is the perimeter of the rectangle on the coordinate graph?
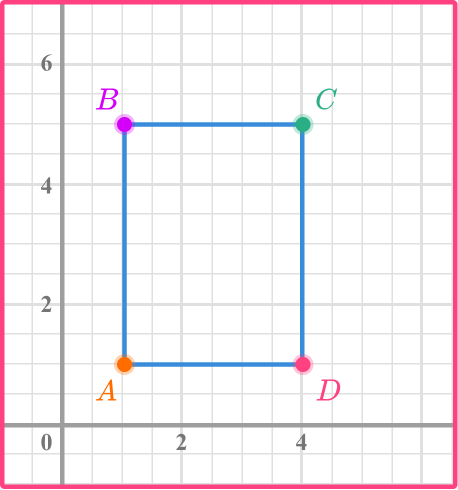
Add all the side lengths or apply the formula.
Counting the units, the length of the rectangle is 6 units and the width of the rectangle is 8 units.
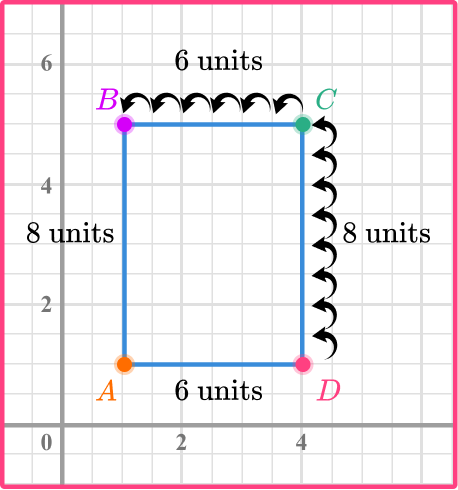
To find the perimeter, add up all the side lengths.
6+6+8+8=28
OR
You can use the formula to find the perimeter of a rectangle; P=2 l+2 w .
l=6 \text { and } w=8
\begin{aligned}& P=2(6)+2(8) \\\\ & P=12+16 \\\\ & P=28\end{aligned}
Write the final answer with the correct units.
The perimeter of the rectangle on the coordinate graph is 28 units.
Example 4: perimeter of the parallelogram
What is the perimeter of the parallelogram?

Add all the side lengths or apply the formula.
Similar to a rectangle, the opposite sides of a parallelogram are congruent (equal). So, there are two sides that measure 13 {~cm} and two sides that measure 28 {~cm}.

To find the perimeter, add up all the side lengths.
13+13+28+28=82
Write the final answer with the correct units.
The perimeter of the parallelogram is 82 {~cm} .
Example 5: word problem
A rectangular vegetable garden has a perimeter of 34 feet. The width of the garden is 11 {~ft} . Find the length of the garden.
Add all the side lengths or apply the formula.
A rectangle has congruent (equal) opposite sides.
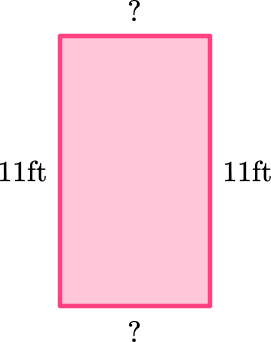
To find the perimeter, add up all the side lengths.
\begin{aligned}& 34=11+11 \; + \; ? \; + \; ? \\\\ & 34=22 \; + \; ? \; + \; ?\end{aligned}
What number will make the equation true?
12 makes the equation true.
22+12=34
Since both sides of the rectangle are equal, 12 is the sum of both sides.
So, 6+6=12
22+6+6=34
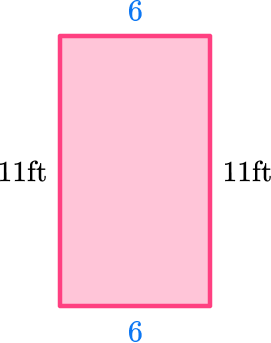
OR you can use the formula to find the length, which is a 7 th grade skill.
You can use the formula to find out the length of the garden.
\begin{aligned}& P=2 l+2 w \\\\
& 34=2 l+2(11) \\\\
& 34=2 l+22 \\\\
& 34-22=2 l+22-22 \\\\
& 12=2 l \\\\
& \cfrac{12}{2}=\cfrac{2 l}{2} \\\\
& 6=l\end{aligned}
Write the final answer with the correct units.
The length of the vegetable garden is 6 {~ft} .
Example 6: perimeter of irregular shape
What is the perimeter of the driveway?
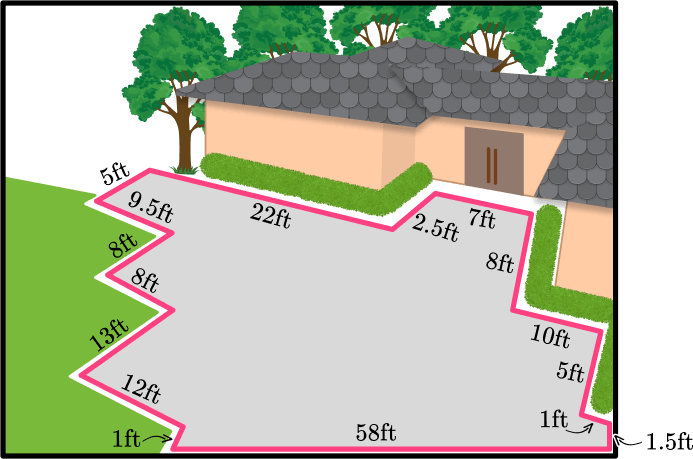
Add all the side lengths.
Choose one of the sides of the driveway to start, and go around the driveway, adding all the side lengths together.
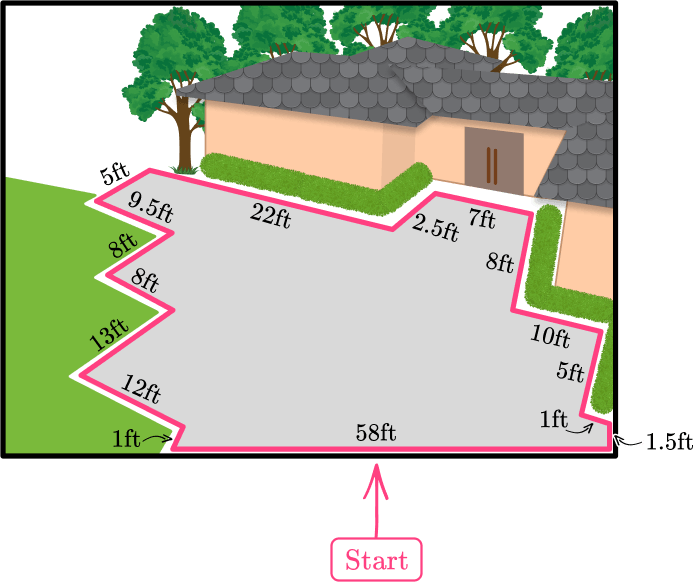
58+1.5+1+5+10+8+7+2.5+22+5+9.5+8+8+13+12+1=171.5
Write the final answer with the correct units.
Each side of the driveway is measured in feet.
The perimeter of the driveway is 171.5 feet.
Teaching tips for how to find the perimeter
- Use active learning activities such as having students measure the perimeter of the classroom or a room in their home. When students are physically active in learning, they tend to retain concepts.
- Choose worksheets that provide a mixture of regular and irregular shapes, both gridded and non-gridded, so students can practice all perimeter solving strategies. This also challenges them to decide which strategies are useful for each type of shape.
- Have students try to identify patterns when finding perimeters of regular polygons.
Easy mistakes to make
- Confusing the concept of area with the concept of perimeter
When students first learn perimeter and area, they can easily mix up the two concepts. Having students do performance tasks that require them to link the concepts to real world scenarios helps build understanding.
- Thinking that the formula for perimeter of a rectangle works for all polygons
Formulas are helpful when making calculations. However, if they are applied haphazardly, it could lead to errors. Having students develop an understanding of formulas through investigative activities prevents them from haphazardly applying formulas to get answers.
- Converting units
In order to find the perimeter, the side lengths have to be the same unit. If the sides are given in different units, convert them all to the same unit before finding the perimeter.
Practice perimeter questions
1. What is the perimeter of the square?





The perimeter is the distance around the square which is the same as summing the four sides. Since a square has four congruent (equal) sides, you can add the four sides up or multiply one side by 4.
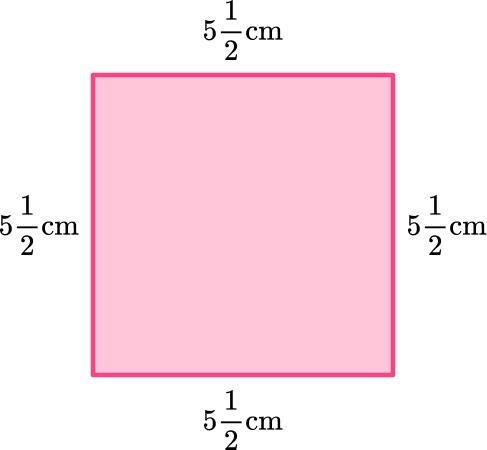
\begin{aligned}& P=5 \cfrac{1}{2}+5 \cfrac{1}{2}+5 \cfrac{1}{2}+5 \cfrac{1}{2} \\\\ & P=22\end{aligned}
OR
\begin{aligned}& P=4 \times 5 \cfrac{1}{2} \\\\ & P=\cfrac{4}{1} \times \cfrac{11}{2} \\\\ & P=\cfrac{44}{2}=22\end{aligned}
The perimeter of the square is 22 {~cm} .
2. The perimeter of an equilateral triangle is 30 units. Find the length of the sides.





An equilateral triangle has 3 congruent (equal) sides. To find the perimeter, you would sum the three sides together. In this case, the perimeter is 30 units.

So, ? \; + \; ? \; + \; ?=30 where the numbers added have to be the same numbers.
Think about the possible side lengths. You know that 10+10+10=30 , so the side lengths of the equilateral triangle are 10 units.
Since the three sides have to be equal, another way to think about it, is what number multiplied by three is equal to 30 .
3 \; \times \; ?=30
The number that makes this equation true is 10 .
Either way you think about it, 10 units is the measure of the side lengths.
3. What is the perimeter of the irregular polygon?
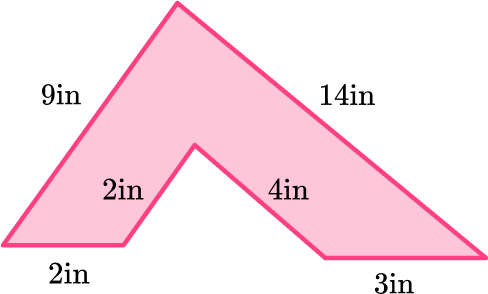




The perimeter is the distance around the entire 2 D shape, which is the same as summing all the sides.
This irregular 2 D shape is a hexagon which means it has six sides. To find the perimeter, sum the six sides.
\begin{aligned}& P=2+2+4+3+14+9 \\\\ & P=34\end{aligned}
The perimeter of the 2 D shape is 34 inches.
4. What is the perimeter of the octagon?





All sides of a regular pentagon are the same length. So the octagon has eight sides that are all 6 {~cm} .
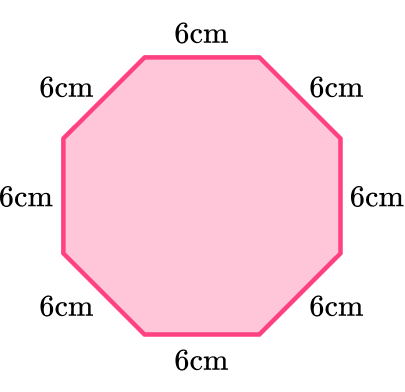
To find the perimeter, find the distance around the octagon which is the same as summing up the side lengths.
6+6+6+6+6+6+6+6=48
Another way to think about it is to multiply one side length by 8 since they are all the same length.
8 \times 6=48
The perimeter of the octagon is 48 {~cm }.
5. The graph below shows a rectangular field on a ranch. The ranch owner wants to fence in the rectangular field. How many yards of fencing does he need? (The coordinates are represented in yards).
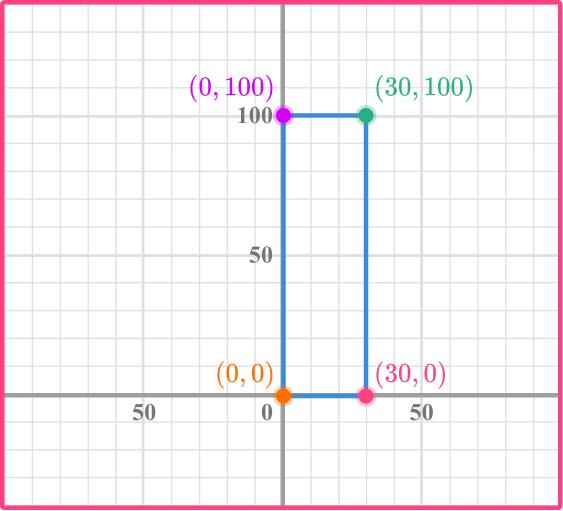




Count the number of spaces from one point to the next. Notice that each grid line is in increments of 10.
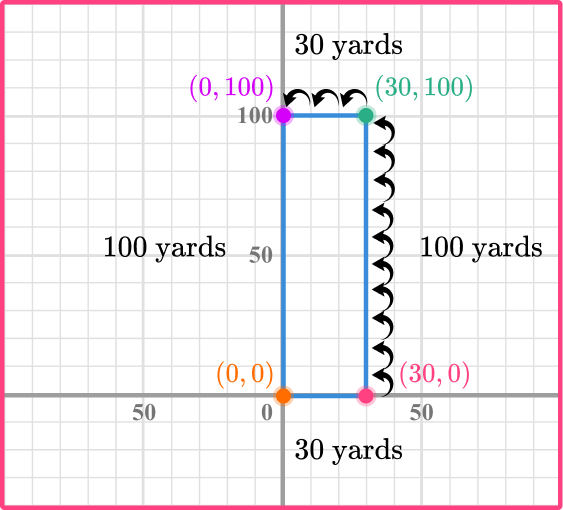
The perimeter is the distance around the rectangle, which is the same as summing the sides.
\begin{aligned}& P=100+100+30+30 \\\\ & P=260\end{aligned}
OR
You can apply the formula for perimeter of the rectangle.
l=30 \text { and } w=100
\begin{aligned}& P=2l+2w \\\\ & P=2(30)+2(100) \\\\ & P=260\end{aligned}
The perimeter is 260 yards which means the rancher needs a total of 260 yards of fencing.
6. This is the pool in the yard at Elvis Presley’s Palm Springs home. Find the perimeter of the pool.
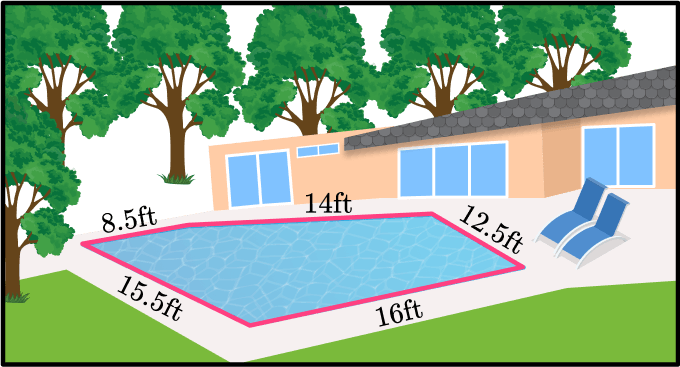




The perimeter is the distance around the figure, which is the same as summing up the sides.
\begin{aligned}& P=8.5+14+12.5+16+15.5 \\\\ & 66.5=8.5+14+12.5+16+15.5\end{aligned}
The perimeter of Elvis’s pool is 66.5 {~ft} .
Perimeter FAQs
Yes, you can find the perimeter or distance around any 2 D shape with straight edges or curved edges. Typically, the perimeter of a circle is called the circumference of a circle. You will learn how to find the circumference of circles in middle school. You will also learn how to find the perimeter of ellipses in high school.
Perimeter is the distance around a rectangle and is measured in units. Area is the space within a rectangle and is measured with square units. They represent different parts of a rectangle, but both require knowing the dimensions of the length and width to solve.
Yes, the side lengths of a polygon can be whole numbers, fractions, or decimals. You would add the fractions together using the rules for adding fractions.
Yes, you can find the perimeter of any quadrilateral or any polygon by summing the side lengths which is finding the total distance around the figure.
The next lessons are
- Symmetry
- Angles in polygons
- Congruence and similarity
- Prism shape
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!