High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
How to find perimeter
Here you will learn how to find perimeter, including what the perimeter of a shape is, how to calculate it for different shapes, and how to solve perimeter word problems.
Students will first learn how to find perimeter as part of measurement and data in 3rd grade and 4th grade.
What is the perimeter?
The perimeter of a 2D shape is the total distance around the outside of the shape.
For example,
Perimeter is measured in units. Each side of the square is one unit.

The perimeter of the rectangle is found by counting the units on each side of the rectangle. You can do this by starting at a vertex and counting each unit around the shape until you arrive back at the vertex.

There are 20 units around the outside of the rectangle, so the perimeter is 20 units.
Notice the perimeter can also be found by adding the length of each side.
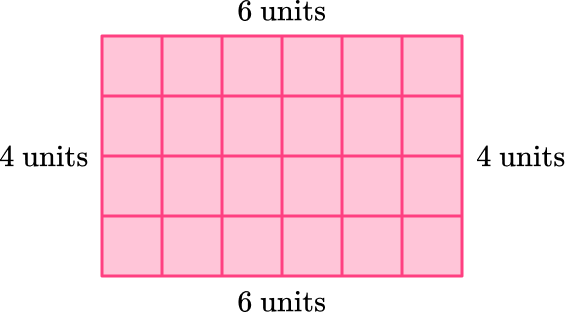
6 + 4 + 6 + 4 = 20, so the perimeter is 20 units.
This addition strategy can be used to find the perimeter for any polygon.
For example,
Find the perimeter of the triangle.
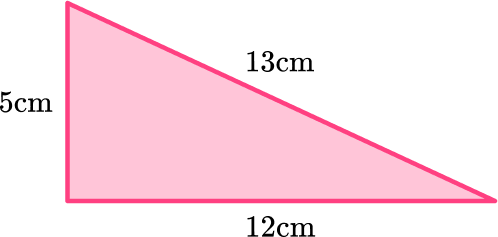
\text{Perimeter }=5+12+13=30 \ \text{ cm}
For example,
Find the perimeter of the parallelogram.

\text{Perimeter }= 8 + 4 + 8 + 4 = 24 units
Note, whenever a specific unit is not given (like cm, m, or km ), the perimeter is labeled ‘units.’
What is the perimeter?
Common Core State Standards
How does this relate to 3rd grade math and 4th grade math?
- Grade 3 – Measurement and data (3.MD.D.8)
Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.
- Grade 4 – Measurement and data (4.MD.A.3)
Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
How to find perimeter
To find the perimeter of a shape:
- Add all the side lengths.
- Write the final answer with the correct units.
![[FREE] Perimeter Check for Understanding Quiz (Grade 3 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Perimeter-listing-image.png)
[FREE] Perimeter Check for Understanding Quiz (Grade 3 to 4)
![[FREE] Perimeter Check for Understanding Quiz (Grade 3 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Perimeter-listing-image.png)
Use this quiz to check your grade 3 to 4 students’ understanding of perimeter. 10+ questions with answers covering a range of 3rd and 4th grade perimeter topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Perimeter Check for Understanding Quiz (Grade 3 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Perimeter-listing-image.png)
[FREE] Perimeter Check for Understanding Quiz (Grade 3 to 4)
![[FREE] Perimeter Check for Understanding Quiz (Grade 3 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Perimeter-listing-image.png)
Use this quiz to check your grade 3 to 4 students’ understanding of perimeter. 10+ questions with answers covering a range of 3rd and 4th grade perimeter topics to identify areas of strength and support!
DOWNLOAD FREEHow to find perimeter examples
Example 1: gridded rectangle
What is the perimeter of the rectangle?

- Add all the side lengths.

The length of the rectangle is 7 units.

The width of the rectangle is 5 units.

The opposite sides of the rectangle are congruent (equal).
To find the perimeter (the total distance around the rectangle), add all the side lengths:
7 + 5 + 7 + 5 = 24
2Write the final answer with the correct units.
There are no specific units given, so they are just labeled ‘units.’
The perimeter of the rectangle is 24 units.
Example 2: given perimeter – find missing side length
The perimeter of the rectangle is 78 \, m. Find the missing side length.

Add all the side lengths.
The opposite sides of a rectangle are congruent (equal).

So, the perimeter is 34 \, + \, ? \, + \, 34 \, + \, ?=78 \, m.
Since 34 + 34 = 68, the two missing sides make up the rest of the perimeter.
Subtract to see how much more is needed to get to a total perimeter of 78 :
78-68 = 10
So, the combined length of the missing sides is 10.
You need to solve ? \, + \, ? = 10. Since the two sides are congruent, each side must be 5, because 5 + 5 = 10.
Write the final answer with the correct units.
The rectangle is measured in meters (m).
The missing side length is 5 \, m.
Example 3: perimeter of isosceles triangle
What is the perimeter of the triangle?
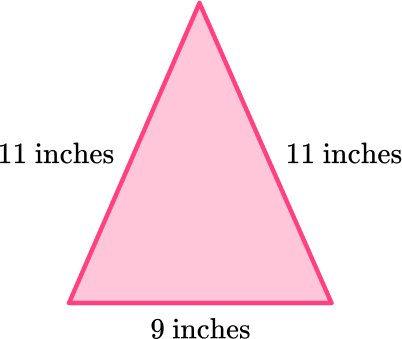
Add all the side lengths.
To find the perimeter (the total distance around the triangle), add all the side lengths:
11 + 11 + 9 = 31
Write the final answer with the correct units.
The triangle is measured in inches.
The perimeter of the triangle is 31 inches.
Example 4: perimeter of a trapezoid
What is the perimeter of the trapezoid?

Add all the side lengths.
To find the perimeter (the total distance around the trapezoid), add all the side lengths:
8+5+6+5=24
Write the final answer with the correct units.
The trapezoid is measured in centimeters (cm).
The perimeter of the trapezoid is 24 \, cm.
Example 5: perimeter of rectilinear shape
What is the perimeter of the polygon?

Add all the side lengths.
When a shape is shown with a grid, the perimeter can be found by counting the total side lengths instead of adding them.
Choose a starting point and count each side around the shape until you reach the starting point again. Be sure to count each unit.
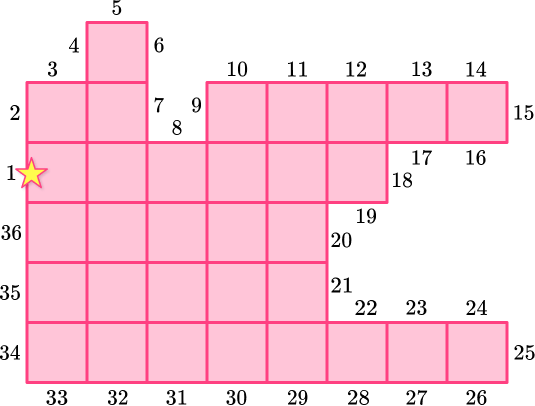
The model above labels each unit, but you don’t need to do this as you solve. The units can also be counted out loud.
Also, notice the star on the first unit. It can be helpful to mark where you start counting so you don’t forget where to stop.
Write the final answer with the correct units.
There are no specific units given, so they are just labeled ‘units.’
The perimeter of the polygon is 36 units.
Example 6: perimeter of rectilinear shape
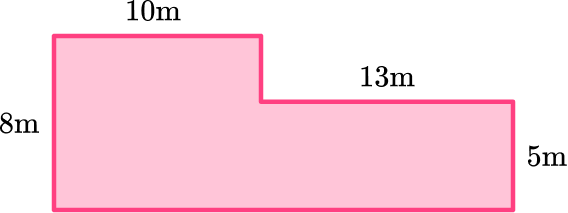
Add all the side lengths.
There are missing measurements in the polygon. You can use what you know about other sides to find the length of the sides.
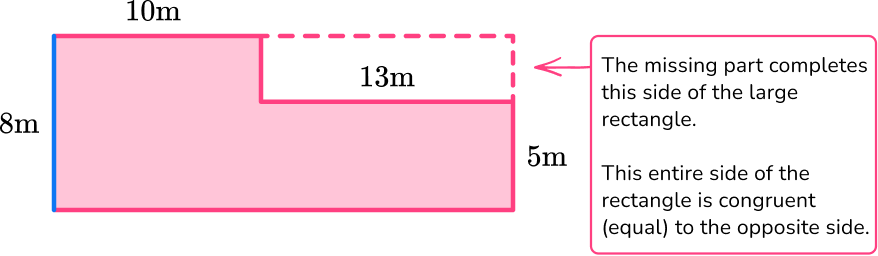
Since 5 + 3 = 8, the missing measurement is 3 \, m.
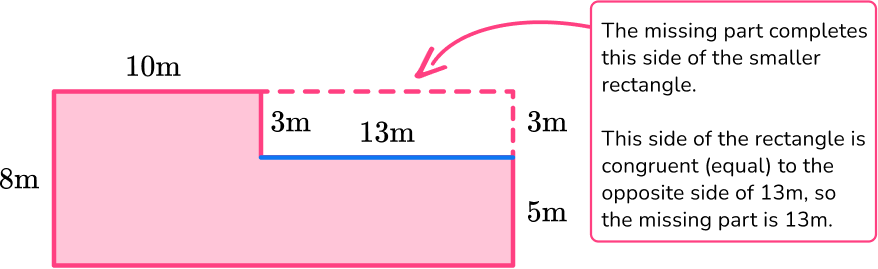
To find the total length of the large rectangle, add 10 \, m and 13 \, m.
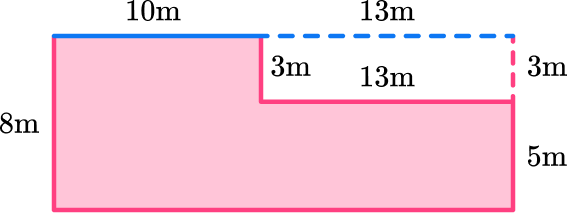
10 + 13 = 23
The missing length of the large rectangle is 23 \, m.
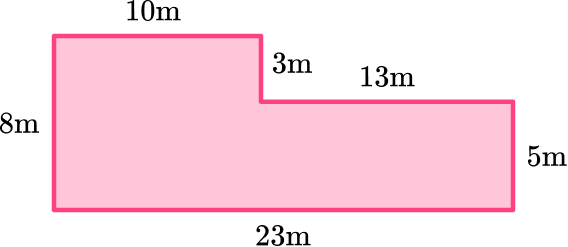
Now that all side lengths are known, add them all to find the perimeter.
8 + 10 + 3 + 13 + 5 + 23 = 62
Write the final answer with the correct units.
The polygon is measured in meters (m).
The perimeter of the polygon is 62 \, m.
Teaching tips for how to find the perimeter
- Choose worksheets that provide a mixture of regular and irregular shapes, both gridded and non-gridded, so students can practice all perimeter solving strategies. This also challenges them to decide which strategies are useful for each type of shape.
- Encourage students to look for patterns or extend known patterns to include perimeter. For example, recognizing that all triangles will have 3 sides to add, and all quadrilaterals will have 4 sides to add, etc. This also includes patterns seen with the calculating perimeter formulas.
For example, you may keep an anchor chart of equations used to find the area of different rectangles. If you consistently ask students to look for patterns, they will eventually notice that the same numbers are being added and some students will connect this to doubling or multiplying numbers. You can then use this as the basis for introducing the formula for the perimeter of a rectangle: 2l+2w =p.
Easy mistakes to make
- Thinking the order of adding the sides matters
Since addition is commutative, it doesn’t matter the order in which the sides of the shape are added. Adding in any order will result in the same answer as long as all sides are added only once.
- Confusing the formulas or solving strategies for perimeter with area
Since they are often introduced together, in the beginning it is easy to confuse the two vocabulary words and/or concepts. After enough exposure and intentional classroom discourse, students will understand and remember the difference.
- Confusing the units for perimeter with area
If students do not have a complete understanding of why perimeter is units and area is square units, they may mix up when to use each. Providing opportunities such as physically measuring the perimeter of items and working with area on grids, can help build an understanding of the difference.
- Confusing the units
In order to add the sides together, they need to be in the same units. If the sides are given in different units, convert to one common unit before adding.
Related perimeter lessons
Practice how to find perimeter questions
1. What is the perimeter of the rectangle?

20 units

24 units

12 units

4 units

The perimeter is the total distance around the outside of the rectangle.

The length of the rectangle is 10 units.

The width of the rectangle is 2 units.
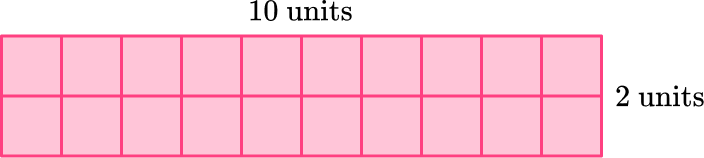
The opposite sides of the rectangle are congruent (equal).
To find the perimeter (the total distance around the rectangle), add all the side lengths:
10 + 2 + 10 + 2 = 24
The perimeter of the rectangle is 24 units.
You can also count each unit of the rectangle to find the perimeter:

2. The perimeter of the rectangle is 94 \, cm. Find the missing side length.





The opposite sides of a rectangle are congruent (equal).

So, the perimeter is ? \, + \, 21 \, + \, ? \, + \, 21 = 94 \, cm.
Since 21 + 21 = 42, the two missing sides make up the rest of the perimeter.
Subtract to see how much more is needed to get to a total perimeter of 94 :
94-42 = 52
So, the combined length of the missing sides is 52.
You need to solve ? \, + \, ? = 52.
Since the two sides are congruent, each side must be 26, because 26 + 26 = 52.
The missing side length is 26 \, cm.
3. What is the perimeter of the hexagon?





To find the perimeter (the total distance around the hexagon), add all the side lengths:
10 + 4 + 4 + 10 + 4 + 4 = 36
The hexagon is measured in feet (ft).
The perimeter of the hexagon is 36 \, ft.
4. What is the perimeter of the regular pentagon?

7 inches

49 inches

28 inches

35 inches

All sides of a regular pentagon are the same length.
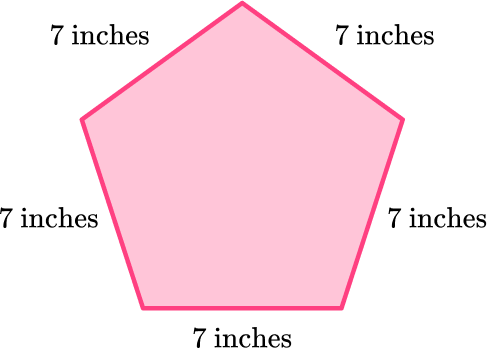
To find the perimeter (the total distance around the pentagon), add all the side lengths:
7 + 7 + 7 + 7 + 7 = 35
The pentagon is measured in inches.
The perimeter of the pentagon is 35 inches.
5. What is the perimeter of the polygon?

28 units

24 units

26 units

30 units

When a shape is shown with a grid, the perimeter can be found by counting the total side lengths instead of adding them.
Choose a starting point and count each side around the shape until you reach the starting point again. Be sure to count each unit.
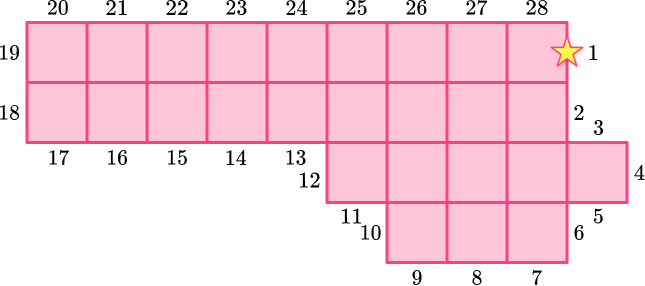
There are no specific units given, so they are just labeled ‘units.’
The perimeter of the polygon is 28 units.
6. What is the perimeter of the polygon?
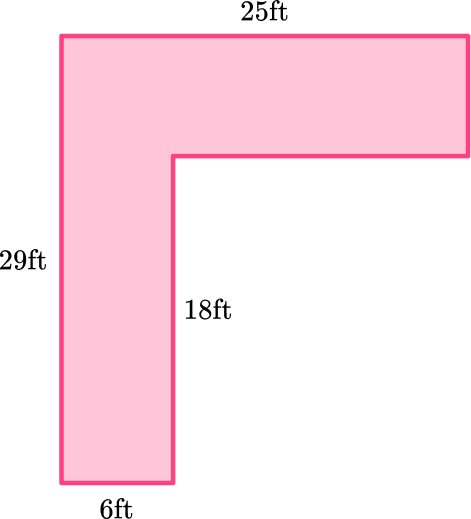




There are missing measurements in the polygon. You can use what you know about other sides to find the length of the sides.
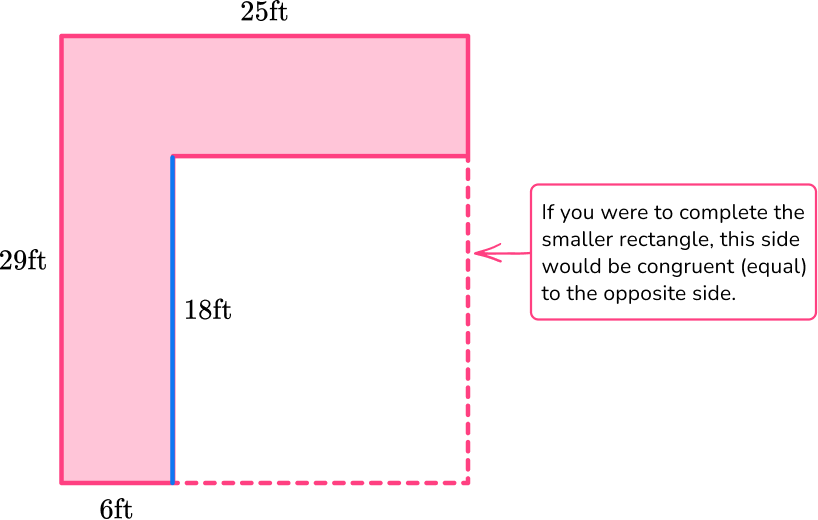
The missing side on the smaller rectangle is 18 \, ft.
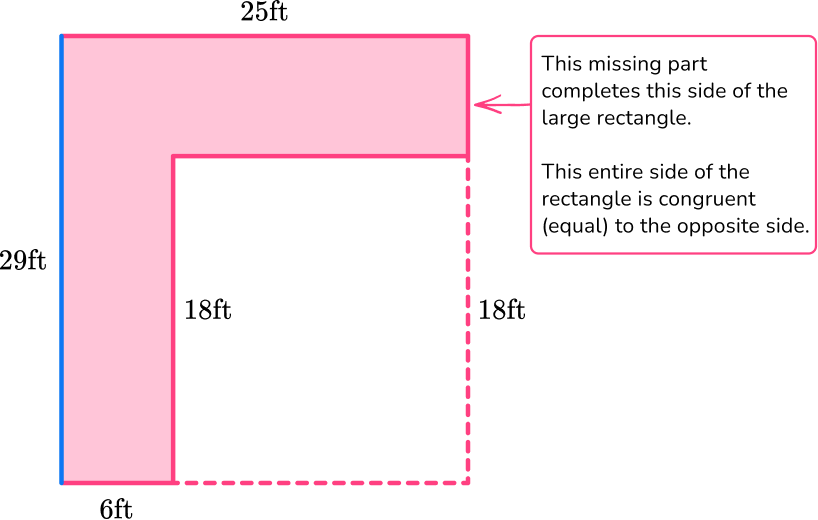
To find the missing side, solve ? \, + \, 18 = 29.
The missing side must be 11, since 11 + 18 = 29.
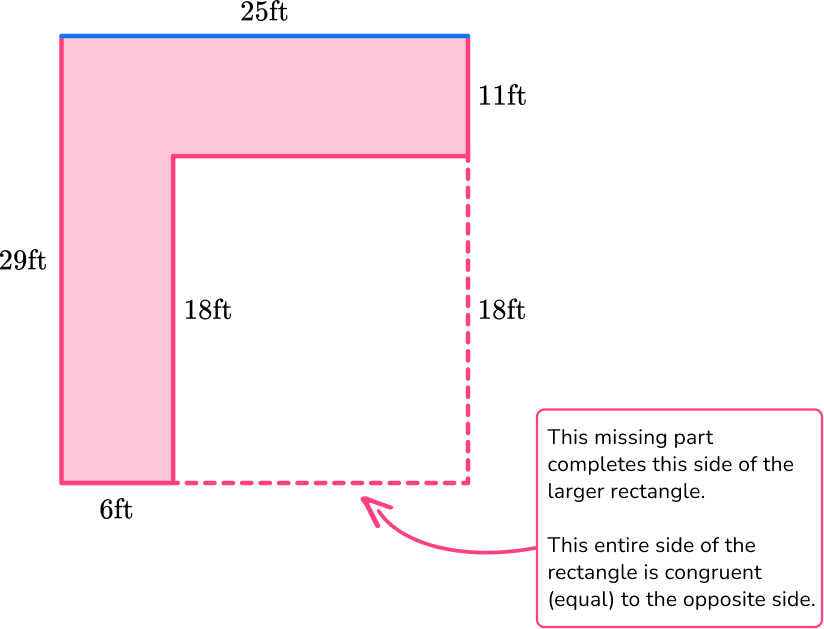
To find the missing side, solve 6 \, + \, ? = 25.
The missing side must be 19, since 6 + 19 = 25.
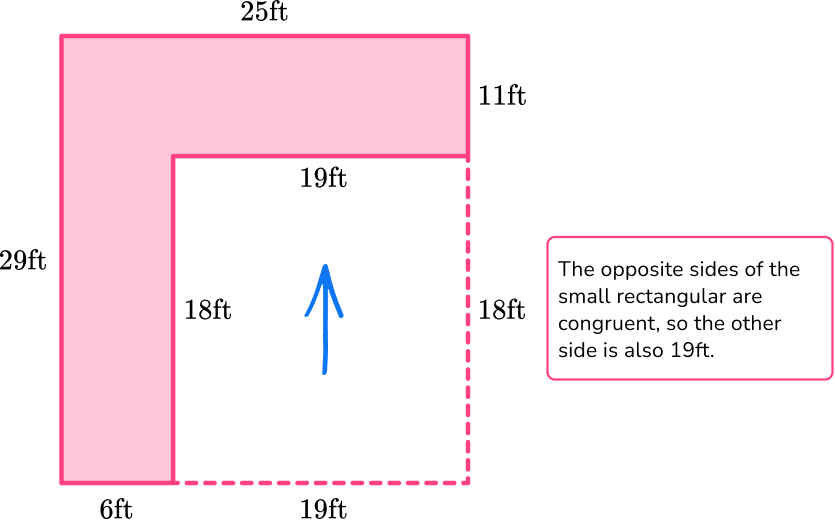
Now that all side lengths are known, add them all to find the perimeter. Remember to only add the side lengths of the polygon.
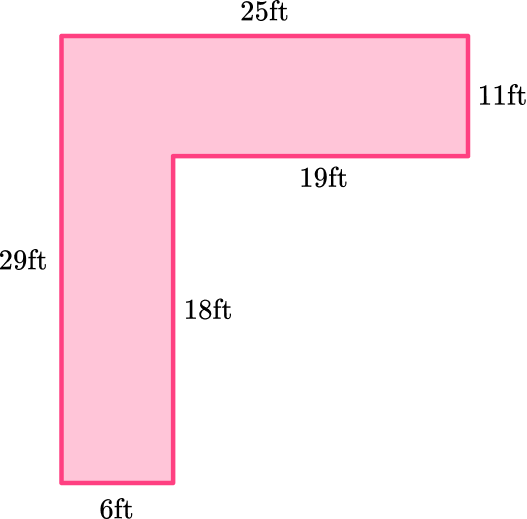
6 + 29 + 25 + 11 + 19 + 18 = 108.
The polygon is measured in feet (ft).
The perimeter of the polygon is 108 \, ft.
How to find perimeter FAQs
In upper grades, students learn how to find the perimeter of a circle. They also learn how to use the distance formula to calculate the perimeter of regular and irregular polygons.
Perimeter is the distance around a rectangle and is measured in units. Area is the space within a rectangle and is measured in square units. They represent different parts of a rectangle, but both require knowing the dimensions of the length and width to solve.
Perimeter is the distance around a triangle and is measured in units (such as feet). Area is the space within a triangle and is measured in square units (such as square feet). For both, you need to know the base length, but other parts of the formulas vary.
The next lessons are
- Symmetry
- Angles in polygons
- Congruence and similarity
- Prism shape
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!