[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Quadrilateral Types of quadrilaterals Multiplication and division Area of a square Area of a rectangle Area of a triangleArea of a quadrilateral
Here you will learn about the area of a quadrilateral, including how to find the area of a rectangle, square, parallelogram, and trapezoid.
Students will first learn about the area of a quadrilateral as part of measurement and data in third grade when they learn about the area of a rectangle.
They expand on this knowledge into 6th grade when they learn how to calculate the area of more complex shapes, such as parallelograms and trapezoids.
What is the area of a quadrilateral?
The area of a quadrilateral is the amount of space inside a quadrilateral.
To find the area of a quadrilateral, you can either count the number of unit squares within a shape or use the appropriate area formula for that shape.
Area is measured in square units. For example, square feet (ft^2), square inches (in^2), square meters (m^2), etc.
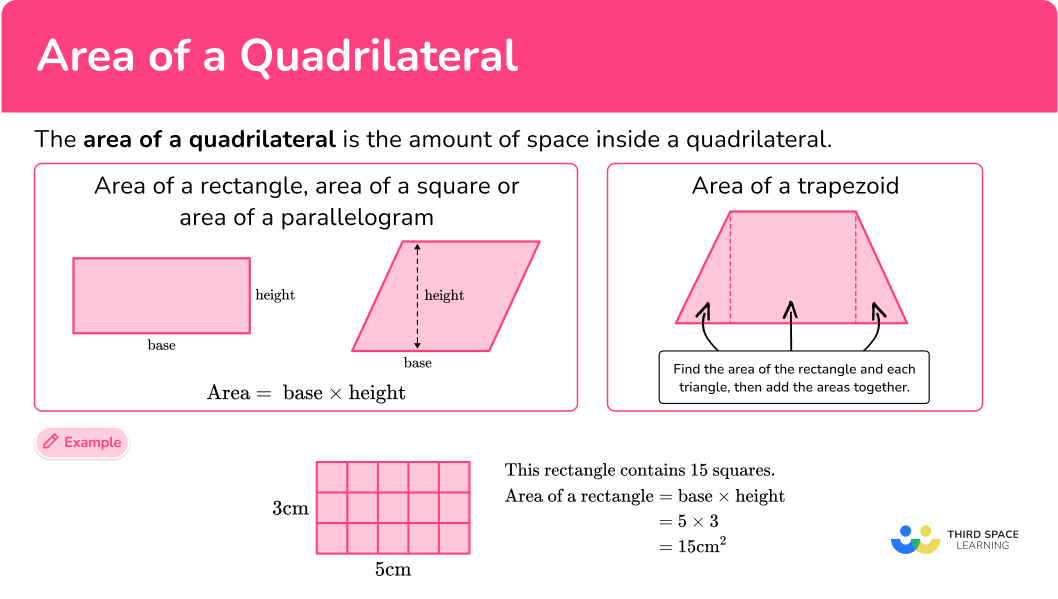
Area of a rectangle or area of a square
Area of a rectangle or area of a square = \text { base } \times \text { height }

For example,
 | This rectangle contains 15 squares.
|
Area of a parallelogram
Area of a parallelogram = \text { base } \times \text { height }
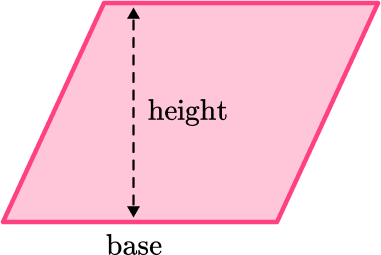 |  If we chop one end off of a parallelogram and rearrange it, |
Step-by-step guide: Area of a parallelogram
Area of a trapezoid
A trapezoid is a quadrilateral with only one pair of parallel sides.
In order to find the area of a trapezoid, you need to decompose the shape into a rectangle and two triangles (or a rectangle and one triangle if it is a right trapezoid).
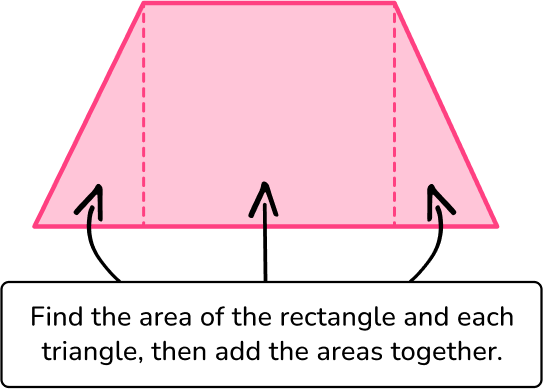
Step-by-step guide: Area of a trapezoid
![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Worksheet (Grade 4 to 6)
![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your students’ understanding of area of a quadrilateral. 15+ questions with answers covering a range of 4th, 5th and 6th grade area topics to identify learning gaps!
DOWNLOAD FREE![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Worksheet (Grade 4 to 6)
![[FREE] Area Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your students’ understanding of area of a quadrilateral. 15+ questions with answers covering a range of 4th, 5th and 6th grade area topics to identify learning gaps!
DOWNLOAD FREEWhat are quadrilaterals?
A quadrilateral is a closed 2 dimensional shape with 4 straight sides and 4 vertices.
Regular quadrilaterals have sides that are all the same length and interior angles that are the same size.
Irregular quadrilaterals have sides that have different lengths and interior angles that have different sizes.
There are several different types of quadrilaterals.
For example,
Square
A square is a closed 2 dimensional shape with four straight sides of equal length and four right angles (90 ^{\circ}) .

Rectangle
A rectangle is a closed 2 dimensional shape with four straight sides and four right angles (90^{\circ}) . It has two pairs of parallel sides that are equal.

Parallelogram
A parallelogram is a closed 2 dimensional shape with four straight sides. The opposite sides of a parallelogram have the same lengths and are parallel.

Rhombus
A rhombus is a parallelogram with four equal straight sides.

Trapezoid
A trapezoid, also known as a trapezium, is a closed 2 dimensional shape with four straight sides and only one pair of parallel sides.

Step-by-step guide: Area of rhombus
What is the area of a quadrilateral?
Common Core State Standards
How does this relate to 6th grade math?
- Grade 6 – Geometry (6.G.1)
Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
How to calculate the area of a quadrilateral
In order to calculate the area of a rectangle, area of a square, or the area of a parallelogram:
- Substitute the values into the formula. (Make sure the units are the same for all measurements.)
- Complete the calculation.
- Add the correct units.
In order to calculate the area of a trapezoid:
- Decompose the shape into a rectangle and two triangles (or one triangle if it is a right trapezoid).
- Find the area of each shape.
- Add the areas together.
- Add the correct units.
Area of a quadrilateral examples
Example 1: area of a square
Find the area of the square:
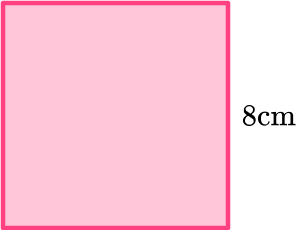
- Substitute the values into the formula. (Make sure the units are the same for all measurements.)
Here the height is 8 . Since it is a square, the base is also 8 .
\begin{aligned}\text { Area } &=\text { base } \times \text { height } \\\\ \text { Area }&=8 \times 8\end{aligned}
2Complete the calculation.
\begin{aligned} & \text { Area }=8 \times 8 \\\\ & \text { Area }=64\end{aligned}
3Add the correct units.
The measurements on this square are in cm so the area will be measured in {cm}^2 .
\text { Area }=64 \mathrm{~cm}^2
Example 2: area of a rectangle, different units
Find the area of the rectangle:

Substitute the values into the formula. (Make sure the units are the same for all measurements.)
Here the base is 11 \, m and the height is 400 \, cm .
Notice that the base measurement is in meters and the height measurement is in centimeters.
The easiest thing to do here is to change 400 \, cm to 4 \, m so that both measurements are in meters.
(You could also change 11 \, m to 1,100 \,cm ).
\begin{aligned}\text { Area }&=\text { base } \times \text { height } \\\\ \text { Area }&=11 \times 4
\end{aligned}

Complete the calculation.
\begin{aligned} & \text { Area }=11 \times 4 \\\\ & \text { Area }=44\end{aligned}
Add the correct units.
The measurements on this rectangle are in m so the area will be in {m}^2 .
\text { Area }=44 \mathrm{~m}^2
Example 3: area of a parallelogram
Calculate the area of the parallelogram:
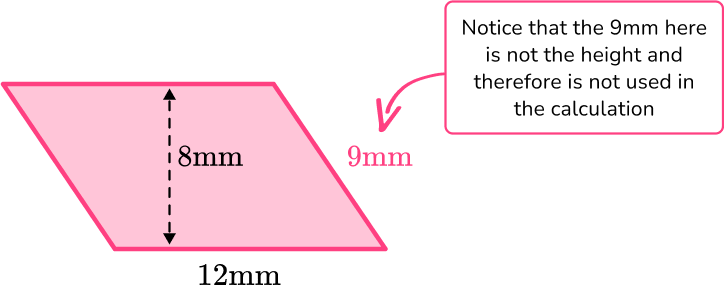
Substitute the values into the formula. (Make sure the units are the same for all measurements.)
\begin{aligned}\text { Area }&=\text { base } \times \text { height } \\\\ \text { Area }&=12 \times 8 \end{aligned}
Complete the calculation.
Area = 96
Add the correct units.
The measurements on this parallelogram are in mm so the area will be in {mm}^2 .
\text { Area }=96 \mathrm{~mm}^2
Example 4: area of a rhombus
Calculate the area of the rhombus:

Substitute the values into the formula. (Make sure the units are the same for all measurements.)
\begin{aligned}\text { Area }&=\text { base } \times \text { height } \\\\ \text { Area }&=10 \times 12 \end{aligned}
Complete the calculation.
Area = 120
Add the correct units.
The measurements on this rhombus are in inches so the area will be {in}^2 .
\text { Area }=120 \mathrm{~in}^2
Example 5: area of a trapezoid
Find the area of the following trapezoid:
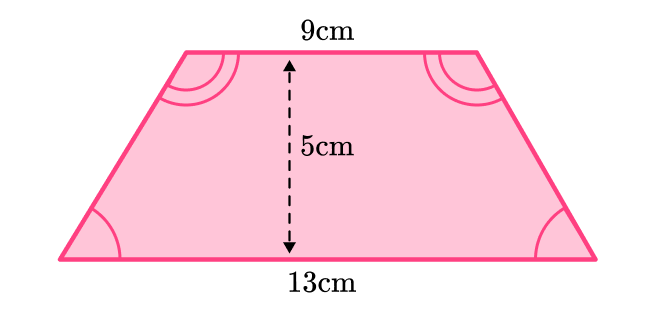
Decompose the shape into a rectangle and two triangles (or one triangle if it is a right trapezoid).
You can use the given measurements to label the base and height of the rectangle and each triangle.
You can also label each shape using the letters A, B , and C .
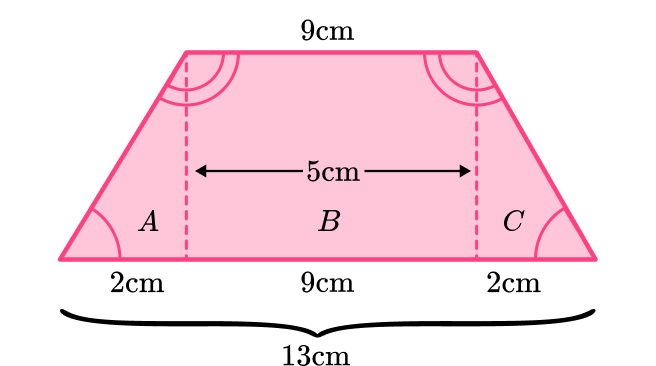
Find the area of each shape.
Shape A (triangle):
\begin{aligned}& \text { Area }=\cfrac{1}{2} \, b h \\\\ & \text { Area }=\cfrac{1}{2} \,(2 \times 5) \\\\ & \text { Area }=5\end{aligned}
Shape B (rectangle):
\begin{aligned}& \text { Area }=\text { base } x \text { height } \\\\ & \text { Area }=9 \times 5 \\\\ &\text { Area }=45\end{aligned}
Shape C (triangle):
\begin{aligned}& \text { Area }=\cfrac{1}{2} \, b h \\\\ & \text { Area }=\cfrac{1}{2} \, (2 \times 5) \\\\& \text { Area }=\cfrac{1}{2} \, \times 10 \\\\ & \text { Area }=5\end{aligned}
Add the areas together.
Add the area of the rectangle to the area of each triangle.
\begin{aligned}& \text { Area }=5+45+5 \\\\ & \text { Area }=55\end{aligned}
Add the correct units.
The measurements on this trapezoid are in cm , so the area will be in {cm}^2 .
\text { Area }=55 \mathrm{~cm}^2
Example 6: area of a right trapezoid
Find the area of the following trapezoid:
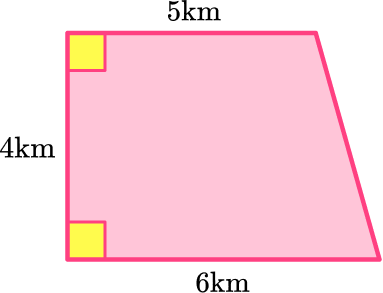
Decompose the shape into a rectangle and two triangles (or one triangle if it is a right trapezoid).
Since this is a right trapezoid, it will need to be decomposed into a rectangle and one triangle. Label the two new shapes A and B .
Find the area of each shape.
Shape A (rectangle):
\begin{aligned}& \text { Area }=\text { base } x \text { height } \\\\ & \text { Area }=4 \times 5 \\\\ & \text { Area }=20\end{aligned}
Shape B (triangle):
\begin{aligned}& \text { Area }=\cfrac{1}{2} \, b h \\\\ & \text { Area }=\cfrac{1}{2} \,(4 \times 1) \\\\ & \text { Area }=\cfrac{1}{2} \times 4 \\\\ & \text { Area }=2\end{aligned}
Add the areas together.
\begin{aligned}& \text { Area }=20+2 \\\\ & \text { Area }=22\end{aligned}
Add the correct units.
The measurements on this trapezoid are in km so the area will be in {km}^2 .
\text { Area }=22 \mathrm{~km}^2
Teaching tips for area of a quadrilateral
- Provide students with study material to help them keep track of the different types of quadrilaterals and how to find the area of each one.
- Once students are comfortable finding the area of a quadrilateral using the area formula, challenge them by asking them to find the area of a quadrilateral where all sides are decimals or fractions.
- Be sure to add a real-world context to area of a quadrilateral problems as often as possible to provide students with a deeper understanding of the concept.
Easy mistakes to make
- Calculating perimeter instead of area
Students often confuse the terms area and perimeter and will sometimes add all sides of a shape in order to find the perimeter instead of finding the area.
- Using a side length as the height of a parallelogram
Students may mistake the side length of a parallelogram for its height.
- Not converting different units so all units are the same
It is very important to make sure the units are the same for each length (for example, all centimeters).
Practice area of a quadrilateral questions
1. Quadrilateral ABCD , shown below, is a square. Find the area of the quadrilateral.





You can use the formula to find the area of the quadrilateral.
Since you know it is a square, you know all sides are the same length.
This means that since its height is 3{~m} , its base is also 3{~m} .
You can use these measurements and the area formula base \times height to calculate the area.
\begin{aligned}\text{Area }&=\text{ base }\times \text{ height}\\\\ &= 3 \times 3\\\\ &=9 \mathrm{~m}^{2}\end{aligned}
2. The base of the rectangle shown below is 4 times greater than its height. Find the area of the rectangle.





First, you need to find the height of the rectangle.
The problem states that the base of the rectangle is 4 times greater than its height.
This means you can divide the base measurement by 4 to get the height measurement.
28 \div 4=7
Once you know the height, you can use the formula for the area of a rectangle, which is base \times height .
\begin{aligned}\text { Area }& =\text { base } x \text { height } \\\\ & =28 \times 7 \\\\ & =196 \mathrm{~yd}^{2} \end{aligned}
3. Find the area of the parallelogram. Give your answer in square centimeters.
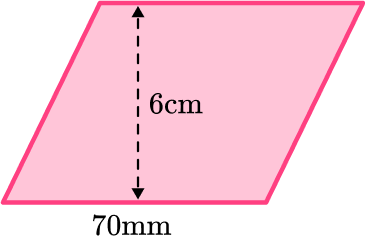




First, you need to make the units the same.
Since 1 {~cm} = 1 {~mm} , you can divide 70 {~mm} by 10 to get its value in cm.
70 {~mm} = 7 {~cm} .
Then you can use the area formula, base \times height .
\begin{aligned} \text{Area }&=\text{ base }\times \text{ height}\\\\ &= 7 \times 6\\\\ &=42 \mathrm{~cm}^{2} \end{aligned}
4. Find the area of the rhombus.
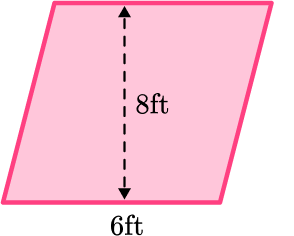




\begin{aligned} \text{Area }&=\text{ base }\times \text{ height}\\\\ &= 6 \times 8\\\\ &=48 \mathrm{~ft}^{2} \end{aligned}
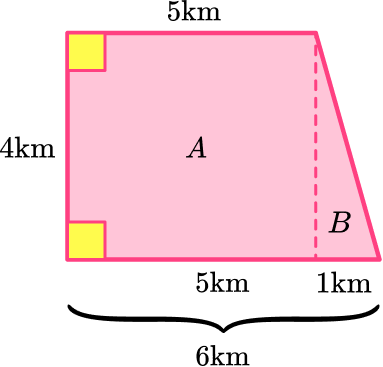
5. Find the area of the trapezoid:




To find the area of the trapezoid, you must first decompose it into a rectangle and two triangles.
Use the area of a rectangle formula and the area of a triangle formula to find the area of each shape.
Then you can add the areas together to find the total area of the trapezoid.
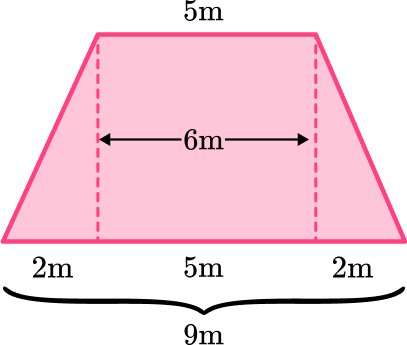
A (triangle):
\begin{aligned} & \text { Area }=\cfrac{1}{2} \, b h \\\\ & \text { Area }=\cfrac{1}{2} \, (2 \times 6) \\\\ & \text { Area }=\cfrac{1}{2} \, \times 12 \\\\ & \text { Area }=6 \end{aligned}
B (triangle):
\begin{aligned} & \text { Area }=\text { base } \times \text { height } \\\\ & \text { Area }=5 \times 6 \\\\ & \text { Area }=30 \end{aligned}
C (triangle):
\begin{aligned} & \text { Area }=\cfrac{1}{2} \, b h \\\\ & \text { Area }=\cfrac{1}{2} \, (2 \times 6) \\\\ & \text { Area }=\cfrac{1}{2} \, \times 12 \\\\ & \text { Area }=6 \end{aligned}
\text { Total area }=6+30+6=42 \mathrm{~m}^2
6. Find the area of the right trapezoid:





First, you need to decompose the right trapezoid into a rectangle and a triangle.

Then, find the area of the rectangle and the area of the triangle using the formulas.
A (rectangle):
\begin{aligned} & \text { Area }=\text { base } \times \text { height } \\\\ & \text { Area }=16 \times 10 \\\\ & \text { Area }=160 \end{aligned}
B (rectangle):
\begin{aligned} & \text { Area }=\cfrac{1}{2} \, b h \\\\ & \text { Area }=\cfrac{1}{2} \, (2 \times 10) \\\\ & \text { Area }=\cfrac{1}{2} \, \times 20 \\\\ & \text { Area }=10 \end{aligned}
Add the area of the rectangle and the area of the triangle. Then add the correct units.
{Area} = 160 + 10
{Area} = 170 \mathrm{~ft}^{2}
Area of a quadrilateral FAQs
A quadrilateral is a closed 2 dimensional shape with 4 straight sides and 4 vertices.
To find the area of a quadrilateral, such as a rectangle, square, or parallelogram, use the area formula which is base \times height .
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!