Area of a Triangle - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Multiplication and division Operations with fractions

Operations with decimals

Area of a rectangle Triangles

Math resources Geometry Area

Area of a triangle

Here you will learn about the area of a triangle, including how to find the area of a triangle with given dimensions.

Students will first learn about area of a triangle as part of geometry in 6th grade.

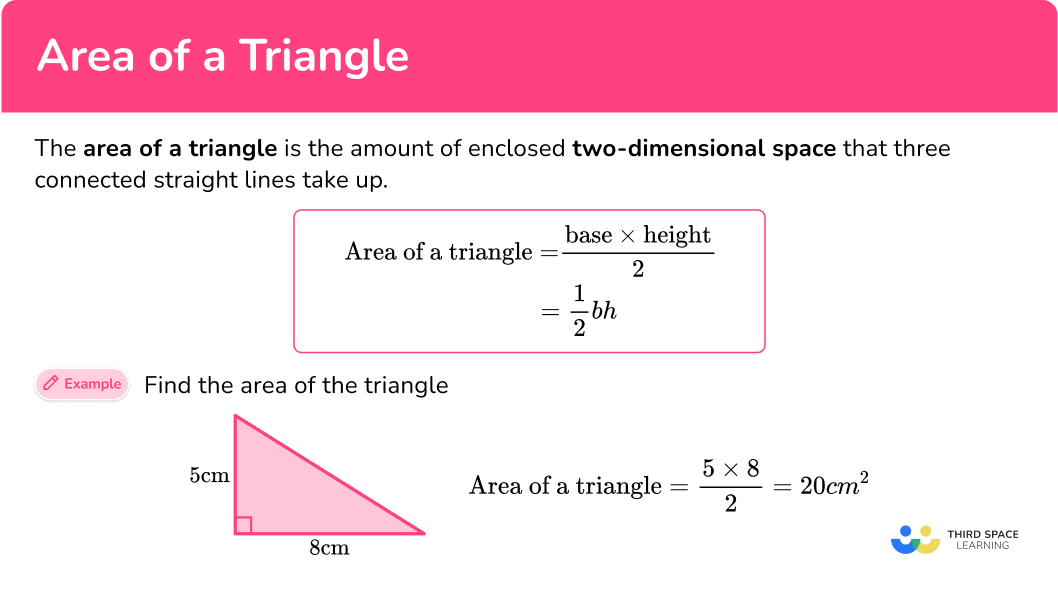
What is the area of a triangle?

The area of a triangle is the amount of enclosed two-dimensional space that three connected straight lines take up.

$\begin{aligned} \text { Area of a triangle } & =\cfrac{\text{ base } \times \text{ height }}{2} \\\\ & =\cfrac{1}{2} \, b h \end{aligned}$

For example,

Find the area of the triangle,

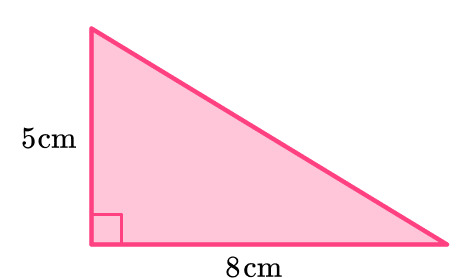
$\text{Area of a triangle}=\cfrac{5 \, \times \, 8}{2}=20 \, cm^2.$

Your final answer must be given in square units. For example $cm^2, m^2,$ or $mm^2.$

In order to find the area of a triangle, you start with the area of a rectangle and divide it by two.

The area of the rectangle below would be calculated by multiplying the base by the height $(b \times h)$ or the length by the width $(l \times w).$ This is pronounced as “base times height” or “length times width,” respectively.

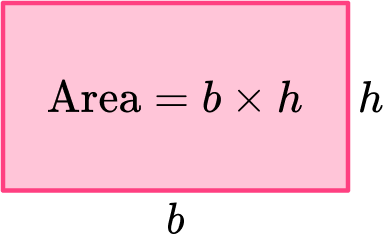
You can draw a diagonal line through the rectangle to create two congruent right triangles.

The area of each triangle is half the area of the rectangle.

On this page, you’ll look at the area of scalene triangles. A scalene triangle is a triangle where all of the sides and all of the angles are different.

This means that a scalene triangle can contain three acute angles, a right angle, or one obtuse angle (and two acute angles).

Acute scalene triangle	Right scalene triangle	Obtuse scalene triangle
$A, \, B, \, C<90^{\circ}$	$C=90^{\circ}$	$C>90^{\circ}$

What is the area of a triangle?

Common Core State Standards

How does this relate to 6th grade math?

Grade 6 – Geometry (6.G.1)
Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.

How to calculate the area of a triangle

In order to calculate the area of a triangle:

Identify the base and perpendicular height of the triangle.
Write the area formula.
Substitute known values into the area formula.
Solve the equation.
Write the answer, including the units.

[FREE] Area Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 5th and 6th grade area topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Area Check for Understanding Quiz (Grade 4 to 6)

DOWNLOAD FREE

Area of a triangle examples

Example 1: right scalene triangle

Calculate the area of the right triangle $ABC.$ Write your answer in square centimeters.

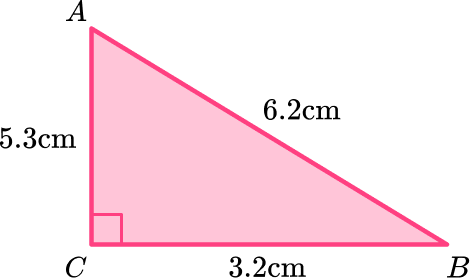
Identify the base and perpendicular height of the triangle.

The sides $AC$ and $BC$ are perpendicular to each other (the angle at $C$ is a right angle), so you can state the values for the base and the perpendicular height of the triangle to be:

The base: $b=3.2 \, cm$

The perpendicular height: $h=5.3 \, cm$

2Write the area formula.

$A=\cfrac{1}{2} \, bh$

3Substitute known values into the area formula.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (3.2)(5.3) \end{aligned}$

4Solve the equation.

Find the value of $A$ by solving the equation:

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (3.2)(5.3)\\\\ &=\cfrac{1}{2} \, \times 3.2\times 5.3\\\\ &=8.48 \end{aligned}$

5Write the answer, including the units.

$A=8.48\text{ cm}^2$

Remember: Your final answer must be in square units.

Example 2: obtuse scalene triangle

For triangle $ABC,$ the angle at $C$ is an obtuse angle, the length $AC=12 \, cm,$ and the height of the triangle is $9 \, cm.$ Calculate the area of triangle $ABC.$

Identify the base and perpendicular height of the triangle.

As $AC$ is perpendicular to the height stated for the triangle, you can state:

$b=12 \, cm$

$h=9 \, cm$

Write the area formula.

$A=\cfrac{1}{2} \, bh$

Substitute known values into the area formula.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (12)(9) \end{aligned}$

Solve the equation.

Solving for $A,$ you have,

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (12)(9)\\\\ &=\cfrac{1}{2} \, \times 12\times 9\\\\ &=54 \end{aligned}$

Write the answer, including the units.

$A=54\text{ cm}^2$

Example 3: acute scalene triangle – mixed units

Calculate the area of triangle $ABC$ below. Write your answer in square meters.

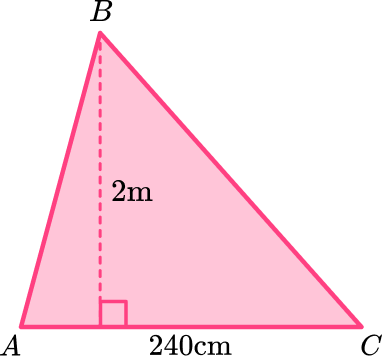
Identify the base and perpendicular height of the triangle.

Currently, you have $2$ different units here. You must convert them to a common unit (here you will use meters as the question requires the answer to be in square meters):

$240 \, cm=2.4 \, m.$

So the base and the perpendicular height of the triangle are:

$b=2.4 \, m$

$h=2 \, m$

Write the area formula.

$A=\cfrac{1}{2} \, bh$

Substitute known values into the area formula.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (2)(2.4) \end{aligned}$

Solve the equation.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (2)(2.4) \\\\ &=\cfrac{1}{2} \, \times 2\times 2.4\\\\ &=2.4 \end{aligned}$

Write the answer, including the units.

$A=2.4\text{ m}^2$

Example 4: obtuse scalene triangle – too much information

$PQR$ is an obtuse scalene triangle. The point $S$ lies on the line $PQ$ such that angle $PSR=90^{\circ}.$ Calculate the area of the triangle $PQR$ below to the nearest hundredth.

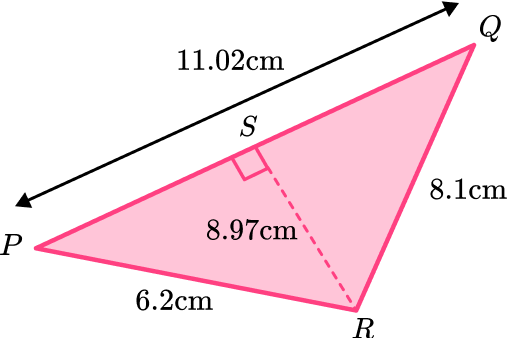
Identify the base and perpendicular height of the triangle.

Here, you need to distinguish which two lengths are perpendicular to one another, as you can use these as the base and the height of the triangle $PQR.$

As the question states that angle $PSR=90^{\circ},$ the side of the triangle $PQ$ is perpendicular to the length $RS,$ which is the height of the triangle. Therefore, you can state:

$b=11.02 \, cm$

$h=8.97 \, cm$

Write the area formula.

$A=\cfrac{1}{2} \, bh$

Substitute known values into the area formula.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (11.02)(8.97) \end{aligned}$

Solve the equation.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (11.02)(8.97)\\\\ &=\cfrac{1}{2} \, \times 11.02 \times 8.97\\\\ &=49.4247 \end{aligned}$

Write the answer, including the units.

$A=49.42 \text{ cm}^2 \text{ (2dp)}$

Example 5: compound shape

A rectangle and a triangle are placed together to make compound shape $ABCDE.$ Calculate the area of the compound shape to the nearest tenth.

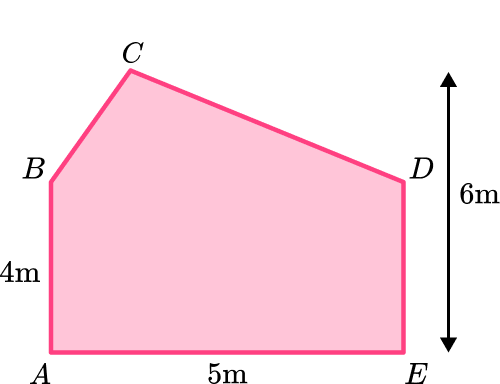
Identify the base and perpendicular height of the triangle.

If you split the compound shape into two polygons, you have a rectangle and a triangle.

As $AB$ and $DE$ are two parallel sides of a rectangle, $AB=DE,$ so you can calculate the vertical height of the triangle by subtracting $4m$ from $6m.$

This gives us the following dimensions on the original diagram:

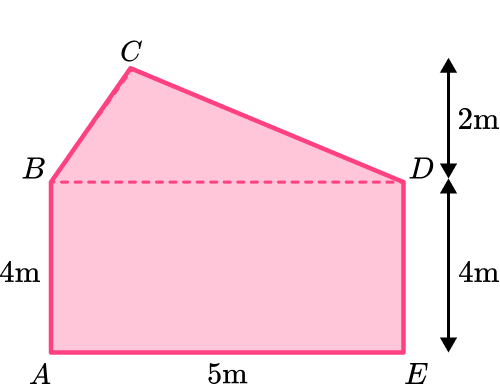
If you sketch another copy of the triangle and label the dimensions of it, you get:

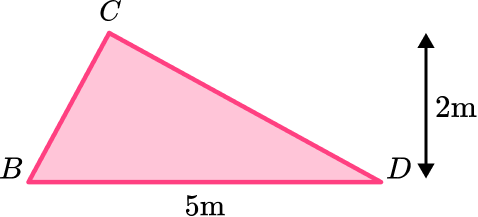
You can now state the values for the base and perpendicular height:

$b=5 \, m$

$h=2 \, m$

Write the area formula.

$A=\cfrac{1}{2} \, bh$

Substitute known values into the area formula.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (5)(2) \end{aligned}$

Solve the equation.

Work out the calculation.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ &= \cfrac{1}{2} \, (5)(2)\\\\ &=\cfrac{1}{2} \, \times 5 \times 2 \\\\ &=5 \end{aligned}$

Now you must find the area of the rectangle.

$\begin{aligned} \text{Area } &=l \times w \\\\ &= 5 \times 4\\\\ &=20 \end{aligned}$

$\text{Total area }=5+20=25$

Write the answer, including the units.

$A=25\text{ m}^2$

How to find a missing side length given the area

Sometimes a question might give you the area and ask you to work out the missing length. In order to do this you must rearrange the formula to make the missing value the subject, and then solve for this letter.

In order to find a missing length given the area:

Write the area formula.
Substitute the known values into the area formula.
Rearrange the equation and solve.
Write the answer, including the units.

Missing side length example

Example 6: calculating the base length given the area

The area of a triangle is $45 \, cm^2.$ The height of the triangle is $10 \, cm.$ Find the length of the base of the triangle.

Write the area formula.

$A=\cfrac{1}{2} \, bh$

Substitute the known values into the area formula.

$\begin{aligned} A &=\cfrac{1}{2} \, bh \\\\ 45&=\cfrac{1}{2} \, \times b\times 10 \end{aligned}$

Rearrange the equation and solve.

You can solve the equation by rearranging to find the unknown $b.$

First, you can tidy up the right side.

$\begin{aligned} 45&=\cfrac{1}{2} \, \times b\times 10\\\\ 45&=b\times 5 \end{aligned}$

Then, you divide both sides by $5.$

$\begin{aligned} 45&=b\times 5\\\\ \frac{45}{5}&=b\\\\ b&=9 \end{aligned}$

Write the answer, including the units.

$b=9\text{ cm}$

Remember: Your final answer must be in linear units only as it is a length.

Teaching tips for area of a triangle

To introduce the formula, give students a rectangular piece of paper and have them cut it into two equivalent right triangles. Then they can physically lay the triangles on top of each other to see that their area is equal, meaning each represents $\cfrac{1}{2}$ of the area of the rectangle. A concrete experience such as this can help them remember the formula.

Give students a variety of types of triangles to work with; triangles with equal sides (equilateral triangles), acute triangles, obtuse triangles, right triangles (also called right-angled triangles), and scalene triangles where the lengths of the sides are different. Show them at different angles and positions so students need to find the base of the triangle and the height of the triangle.

Easy mistakes to make

Incorrectly identifying the dimensions
The base of a triangle and the height of a triangle MUST be at a right angle to each other. They must be perpendicular. You may be given additional sides of a triangle that are not needed. You may also need to rotate the triangle around so that you can identify the base and height more easily.

For example,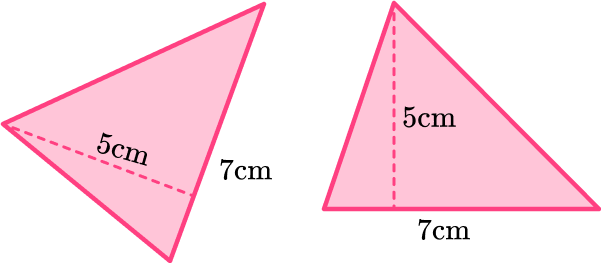

Forgetting to write the units
It is common to forget the units for area in the final answer. When calculating the area of a rectangle, your answer must always have units squared (or square units). This is also written by using the exponent $2$ after the abbreviated units, such as unit $^2.$

Practice area of a triangle questions

8 \text{ cm}^2

7.5 \text{ cm}^2

15 \text{ cm}^2

16 \text{ cm}^2

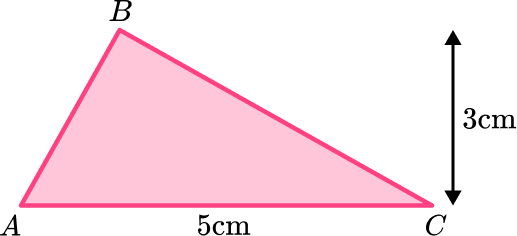
The base and the perpendicular height are $5 \, cm$ and $3 \, cm$ respectively, so the calculation you need to do is:

$\begin{aligned} A&=\cfrac{1}{2} \, bh \\\\ &=\cfrac{1}{2} \, (5)(3)\\\\ &=\cfrac{1}{2} \, \times 5\times 3\\\\ &=7.5 \end{aligned}$

The units will be $cm^2.$

126 \text{ cm}^2

252 \text{ cm}^2

12.6 \text{ cm}^2

25.2 \text{ cm}^2

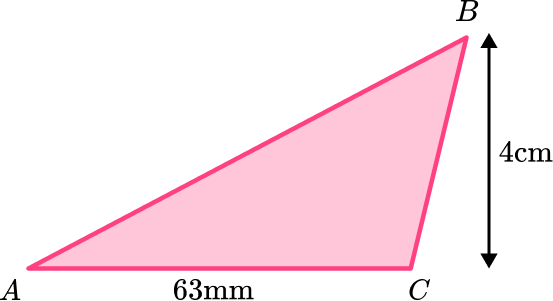
The base is $63 \, mm$ which needs to be converted to $6.3 \, cm.$

The height is $4 \, cm.$

The calculation you need to do is:

$\begin{aligned} A&=\cfrac{1}{2} \, bh \\\\ &=\cfrac{1}{2} \, (6.3)(4)\\\\ &=\cfrac{1}{2} \,\times 6.3 \times 4\\\\ &=12.6 \end{aligned}$

The units will be $cm^2.$

24 \text{ cm}^2

21 \text{ cm}^2

12 \text{ cm}^2

10.5 \text{ cm}^2

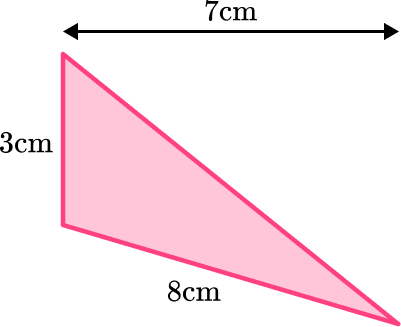
It may be easier to see the base and height if you turn the triangle.

The base and the height are $3 \, cm$ and $7 \, cm.$ The $8 \, cm$ is not needed.

So the calculation you need to do is:

$\begin{aligned} A&=\cfrac{1}{2} \, bh \\\\ &=\cfrac{1}{2} \, (3)(7)\\\\ &=\cfrac{1}{2} \,\times 3 \times 7\\\\ &=10.5 \end{aligned}$

The units will be $cm^2.$

13.8 \text{ m}^2

13 \, 800 \text{ cm}^2

6.9 \text{ m}^2

69 \, 000\text{ cm}^2

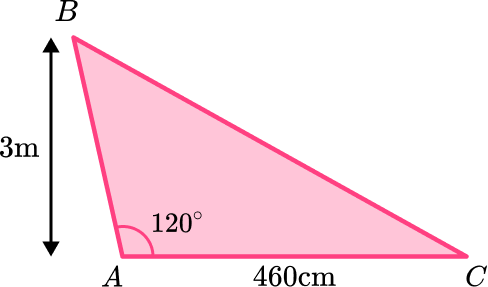
The base is $460 \, cm$ which needs to be converted to $4.6 \, m.$

The height is $3 \, m.$

The calculation you need to do is:

$\begin{aligned} A&=\cfrac{1}{2} \, bh \\\\ &=\cfrac{1}{2} \, (4.6)(3)\\\\ &=\cfrac{1}{2} \,\times 4.6 \times 3 \\\\ &=6.9 \end{aligned}$

The units will be $m^2.$

1250 \text{ m}^2

500 \text{ m}^2

750 \text{ m}^2

2000 \text{ m}^2

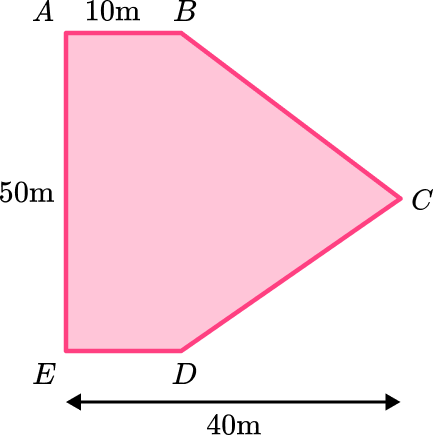
The compound shape is made up of a rectangle and a triangle.

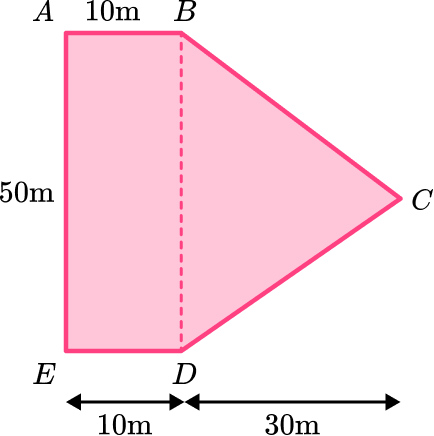
Area of a Triangle image 18 US

The area of the rectangle is $10\times{50}=500\text{ m}^2$

The area of the triangle is:

$\begin{aligned} A&=\cfrac{1}{2} \, bh \\\\ &=\cfrac{1}{2} \, (50)(30) \\\\ &=\cfrac{1}{2} \,\times 50 \times 30 \\\\ &=750 \end{aligned}$

The total area will be $500+750=1250$

The units will be $m^2.$

24 \text{ cm}

12 \text{ cm}

6 \text{ cm}

18 \text{ cm}

The area is $84 \, cm^2$ and the height is $14 \, cm.$

The calculation you need to do is:

$\begin{aligned} A&=\cfrac{1}{2} \, bh \\\\ 84&=\cfrac{1}{2} \, (b)(14)\\\\ 84&=\cfrac{1}{2} \, \times b\times 7\\\\ b&=84\div 7\\\\ b&=12 \end{aligned}$

The units will be $cm.$

Area of a triangle FAQs

What is the area formula for a triangle?

The area formula for a triangle is $A=\cfrac{1}{2} \, b h.$

What is the difference between the area of a triangle and the perimeter of a triangle?

The area of a triangle is the amount of enclosed two-dimensional space inside the shape. The perimeter of a triangle is the length of distance around the outside of the triangle, or the added lengths of the sides of the triangle.

How does the pythagorean theorem relate to the area of a triangle?

The pythagorean theorem can be used to find a missing base or height length to then use the area formula. The pythagorean theorem can be used when the hypotenuse and either the base or height is known. Students substitute the dimensions in to find all three side lengths. Then they use the area formula using the known base and height.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.