High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Multiplication and division Multiplying and dividing decimals Area of a rectangle Area of a parallelogram Area of a triangleArea of composite shapes
Here you will learn about the area of composite shapes, including questions involving rectilinear shapes, composite shapes, missing side lengths and unit conversion.
Students will first learn about composite shapes as part of geometry in 3rd grade when they learn how to decompose and find the area of rectilinear shapes.
Students deepen their understanding of area in 4th grade, and extend their learning by finding the area of more complex shapes in 6th grade.
What is the area of composite shapes?
The area of composite shapes is the amount of space inside a shape composed of basic shapes put together. It is measured in square units ( cm^2, m^2, mm^2 etc.).
Composite shapes can also be called compound shapes or composite figures.
To find the area of composite shapes, you must decompose the composite shape into basic shapes, then find the area of each of the basic shapes and add them together.
For example,
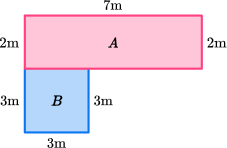 |
|---|
\begin{aligned} \hspace{0.5cm} \text{\color{#f22e76}Area of Shape A} \, + \, \text{\color{#1682e0}Area of Shape B} \, &= \, \text{Area of Compound Shape} \hspace{0.5cm} \\\\ {\color{#f22e76}(7m \times 2m)} \quad + \quad {\color{#1682e0}(3m \times 3m)} \quad \quad \, & = \\\\ {\color{#f22e76}14m^2} \quad \quad + \quad \quad {\color{#1682e0}9m^2} \quad \quad \quad \;\;\; &= \quad \quad \quad 23m^2 \end{aligned} |
Your final answer must be in square units. For example, square centimeters (cm^2), square meters (m^2), square feet (ft^2), etc.
What is the area of composite shapes?
![[FREE] Area of Composite Shapes Worksheet (Grade 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Area-of-Composite-Shapes-Worksheet-listing-image.png)
[FREE] Area of Composite Shapes Worksheet (Grade 3 to 8)
![[FREE] Area of Composite Shapes Worksheet (Grade 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Area-of-Composite-Shapes-Worksheet-listing-image.png)
Use this worksheet to check your grade 3 to 8 students’ understanding of calculating the area of composite shapes. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Area of Composite Shapes Worksheet (Grade 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Area-of-Composite-Shapes-Worksheet-listing-image.png)
[FREE] Area of Composite Shapes Worksheet (Grade 3 to 8)
![[FREE] Area of Composite Shapes Worksheet (Grade 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Area-of-Composite-Shapes-Worksheet-listing-image.png)
Use this worksheet to check your grade 3 to 8 students’ understanding of calculating the area of composite shapes. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 3rd grade math and 4th grade math?
- Grade 3 – Measurement and Data (3.MD.7, 3.MD.7.d)
Relate area to the operations of multiplication and addition; Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.
- Grade 4 – Measurement and Data (4.MD.3)
Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
- Grade 6 – Geometry (6.G.1)
Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
How to find the area of composite shapes
Here’s how to find the area of composite shapes:
- Break down the composite shape into simpler shapes, such as rectangles, triangles, etc.
- Find the measurements and areas of the simpler shapes.
- Add the areas of the simpler shapes together.
- Write down your final answer with square units.
Area of composite shapes examples
Example 1: all side lengths given (area of a rectilinear figure)
Find the area of the composite shape below:
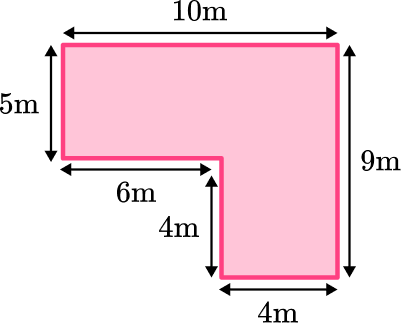
- Break down the composite shape into basic shapes.
Split the composite shape into two rectangles. You can do this in two ways:
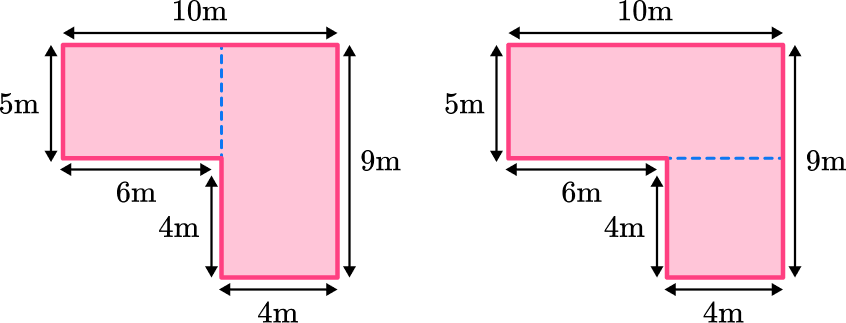
For the purposes of this question you will use the first way.
2Find the measurements and area of the simpler shapes.
Label the two rectangles A and B.
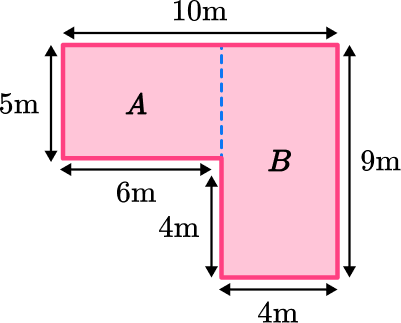
Area of Rectangle A :
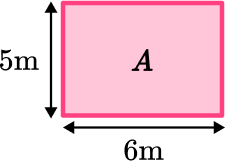
\begin{aligned} \text { Area }_{A} &=\text{ length } \times \text{ width } \\\\ \text { Area }_{A} &=6 \times 5 \\\\ &=30 \end{aligned}
Area of Rectangle B :
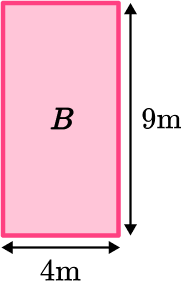
\begin{aligned} \text { Area }_{B} &=\text{ length } \times \text{ width } \\\\ \text { Area }_{B} &=9 \times 4 \\\\ &=36 \end{aligned}
3Add the areas of the simpler shapes together.
\begin{aligned} \text { Composite Area } &=\text{ Area of } A+ \text{ Area of } B \\\\ &= 30+36 \\\\ &=66 \end{aligned}
4Write down your final answer with square units.
\text{ Area }=66 \mathrm{~m}^{2}
Example 2: missing lengths
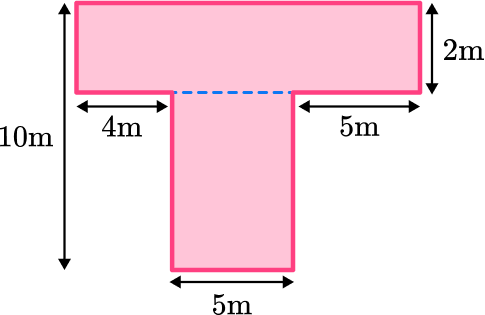
Find the area of the composite shape below:
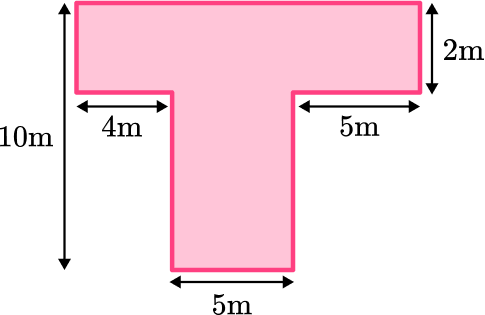
Break down the composite shape into simpler shapes.
Split the composite shape into two rectangles and find the area of each rectangle.
Find the measurements and areas of the simpler shapes.
Label the two rectangles A and B.
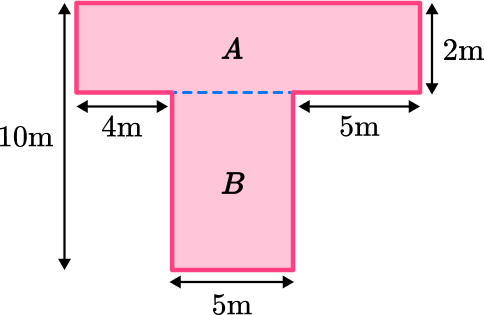
Area of Rectangle A :

You need to calculate the unknown length. To do this, you need to use the measurements you are given in the question that are parallel to the unknown side:
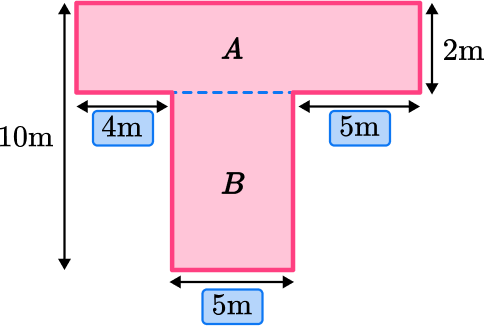
If you add together the 3 sides, you will get the length of rectangle A.
4+5+5= 14 \, m

\begin{aligned} \text { Area }_{A} &=\text{ length } \times \text {width } \\\\ \text { Area }_{A} &=14 \times 2 \\\\ &=28 \end{aligned}
Area of Rectangle B :
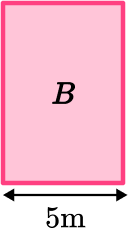
You need to calculate the unknown length. To do this, you need to use the measurements you are given in the question that are parallel to the unknown side:
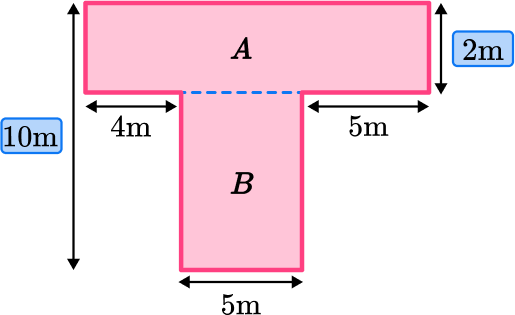
The length of the entire composite shape is 10 \, m. You need to subtract the 2 \, m of shape A to get just the length of shape B.
10-2=8
\begin{aligned} \text { Area }_{B} &=\text{ length } \times \text{ width } \\\\ \text { Area }_{B} &=8 \times 5 \\\\ &=40 \end{aligned}
Add the areas of the simpler shapes together.
\begin{aligned} \text { Composite Area } &=\text{ Area of } A+\text{ Area of } B \\\\ &=28+40 \\\\ &=68 \end{aligned}
Write down your final answer with square units.
\text{ Area }=68 \mathrm{~m}^{2}
Example 3: word problem
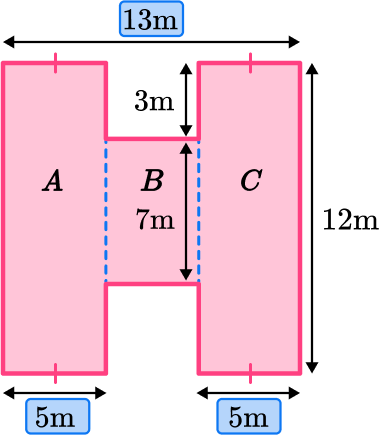
The wall shown below needs to be painted. Each tin of paint covers a distance of 4 square meters. How many tins of paint will be needed to cover the entire wall?
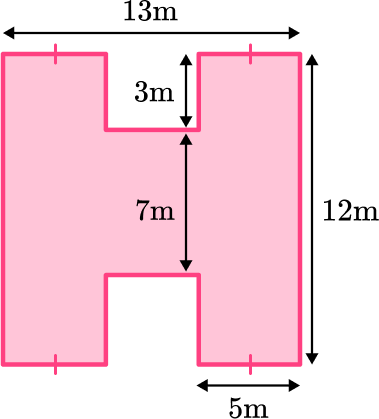
Break down the composite shape into simpler shapes.
Split the composite shape into three rectangles and find the area of each rectangle.
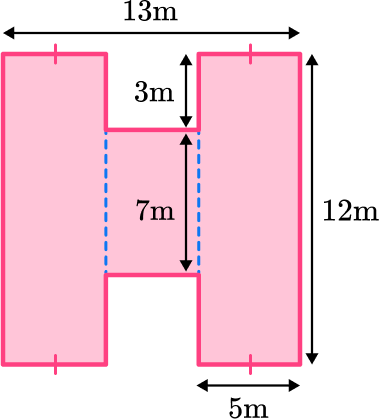
Find the measurements and areas of the simpler shapes.
Label the three rectangles A, B and C.
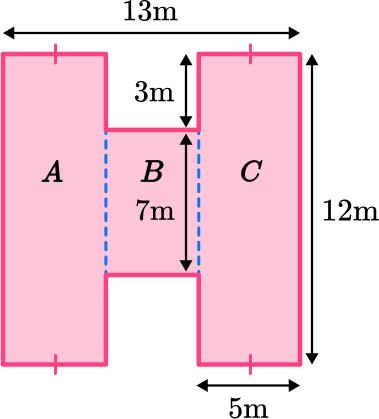
Notice that rectangle A and C each have a tick mark at the bottom. This means that these sides are congruent, or equal. Therefore, we know the width of rectangle A is 5 \, m.
Area of Rectangle A :
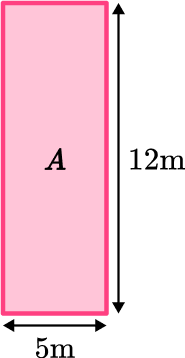
\begin{aligned} \text { Area }_{A} &=\text{ length } \times \text{ width } \\\\ \text { Area }_{A} &=12 \times 5 \\\\ &=60 \end{aligned}
Rectangle C is congruent to Rectangle A, so you can just double the area of rectangle A.
60 \times 2=120
Area of Rectangle B :
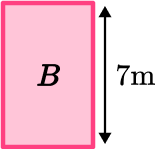
You need to calculate the unknown width. To do this, you need to use the measurements you are given in the question that are parallel to the unknown side:
The entire width of the shape is 13 \, m. If you subtract 5 \, m and 5 \, m \; ( the width of rectangles A and C).
13 - 5 - 5 = 3 \, m
\begin{aligned} \text{ Area }_{B} &=\text { length } \times \text{ width } \\\\ \text{ Area }_{B} &=7 \times 3 \\\\ &=21 \end{aligned}
Add the areas of the simpler shapes together.
\begin{aligned} \text { Composite Area } &=\text{ Area of } A+\text{ Area of } B+\text{ Area of } C \\\\ &=60+21+60 \\\\ &=141 \end{aligned}
Write down your final answer with square units.
\text { Area }=141 \mathrm{~m}^{2}
While this is the total area, you need to calculate how many tins of paint will be needed to cover the wall.
If each tin of paint covers a distance of 4 square meters, you need to divide 4 into 141.
141 \div 4=35.25
Since you cannot buy 0.25 of a can of paint, you need to round your answer to 36 tins of paint.
Answer \textbf{= } \bf{36} tins of paint will be needed.
Example 4: composite shapes involving non-rectangular shapes
Find the area of the composite shape below:
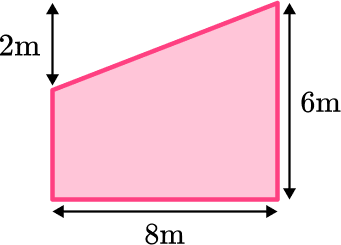
Break down the composite shape into simpler shapes.
Split the composite shape into a triangle and rectangle.
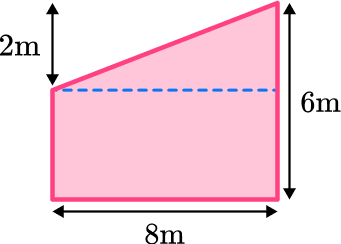
Note: This shape is a trapezoid. Another way to find the area of this shape would be to simply use the formula for the area of a trapezoid. For this question, because you are focusing on composite shapes, you will separate the shape into a triangle and a rectangle.
See also: Area of a trapezoid
Find the measurements and areas of the simpler shapes.
Label the two shapes A and B.
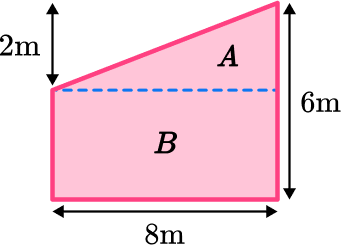
Area of Triangle A :

\begin{aligned}
\text { Area }_{A} &=\cfrac{b \, \times h}{2} \\\\
\text { Area }_{A} &=\cfrac{2 \, \times 8}{2} \\\\
&=8
\end{aligned}
Area of Rectangle B :
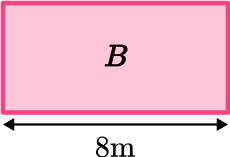
You need to calculate the unknown length. To do this, you need to use the measurements you are given in the question that are parallel to the unknown side:
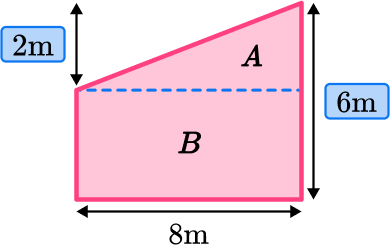
The height of the entire composite shape is 6 \, m. You need to subtract the 2 \, m of shape A to get just the length of shape B.
6-2=4
\begin{aligned}
\text { Area }_{B} &=\text{ length } \times \text{ width } \\\\
\text { Area }_{B} &=8 \times 4 \\\\
&=32
\end{aligned}
Add the areas of the simpler shapes together.
\begin{aligned} \text{ Composite Area } &=\text{ Area of } A+\text{ Area of } B \\\\ &=8+32 \\\\ &=40 \end{aligned}
Write down your final answer with square units.
\text{ Area }=40 \mathrm{~m}^{2}
Example 5: missing side lengths
Calculate the value of x in the composite shape below:
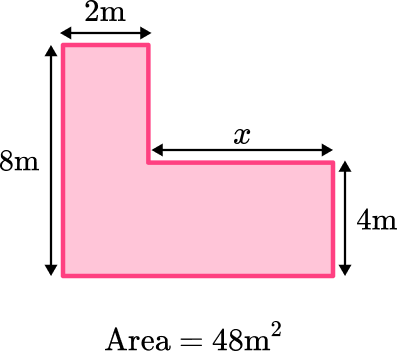
Break down the composite shape into simpler shapes.
Split the composite shape into two rectangles.
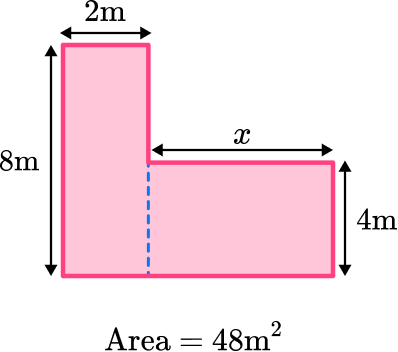
Find the measurements and area of the simpler shapes.
Label the two rectangles A and B.
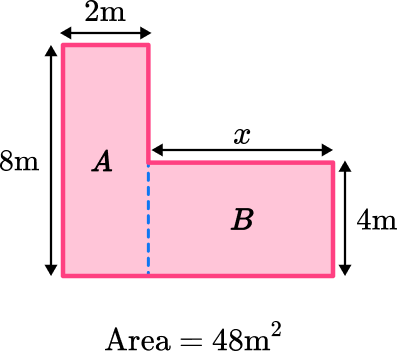
Area of Rectangle A :
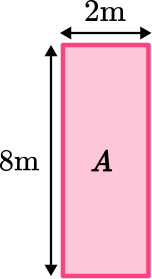
\begin{aligned}
\text { Area }_{A} &=\text{ length } \times \text{ width } \\\\
\text { Area }_{A} &=8 \times 2 \\\\
&=16
\end{aligned}
In this case, you are not given enough information to find the area of Rectangle B.
Add the areas of the simpler shapes.
For this problem, you will need to use subtraction in order to find the area of rectangle B.
\begin{aligned} \text{ Composite Area } &=\text{ Area of } A+\text{ Area of } B \\\\ 48 &=16+\text{ Area of } B \\\\ \text{ Area of } B &=48-16 \\\\ \text{ Area of } B &=32 \end{aligned}
Now that you know the area of rectangle B, you can calculate the value of x.
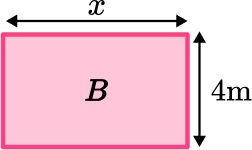
\begin{aligned}
\text{ Area of } B &=l \times w \\\\
32 &=l \times 4 \\\\
l &=\cfrac{32}{4} \\\\
l &=8 \, m
\end{aligned}
x = 8 \, m
Example 6: multi-step word problem
Below is a blueprint for a garden to be created in the middle of town. It will feature a triangular flowerbed and the remainder of the garden will be covered in grass.
Each roll of grass costs \$24 and covers a distance of 3 square meters. How much will it cost to cover the garden with grass?
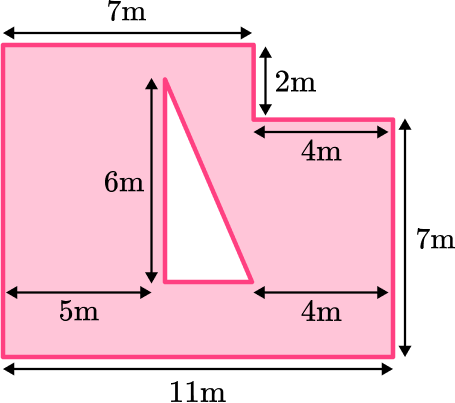
Break down the composite shape into simpler shapes.
Split the composite shape into two rectangles. Once you find the area of the two rectangles, you can subtract the area of the triangle.
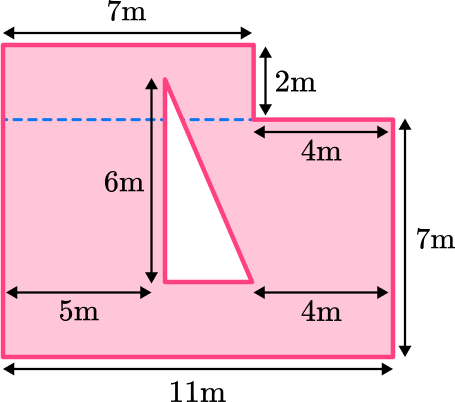
Find the measurements and areas of the simpler shapes.
Label the three shapes A, B and C.
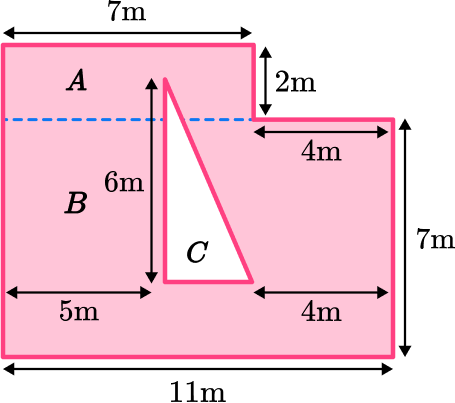
Area of rectangle A :

\begin{aligned} \text { Area }_A & =\text{ length } \times \text{ width } \\\\ \text { Area }_A & =7 \times 2 \\\\ & =14 \mathrm{~m}^2 \end{aligned}
Area of rectangle B :
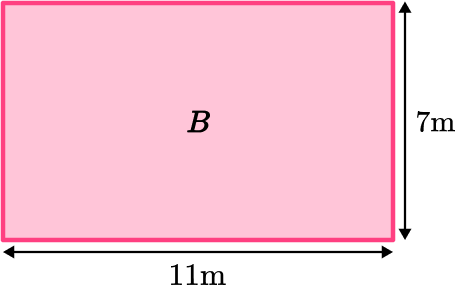
\begin{aligned}
\text{ Area }_{B} &=\text{ length } \times \text{ width } \\\\
\text { Area }_{B} &=11 \times 7 \\\\
&=77 \mathrm{~m}^{2}
\end{aligned}
Area of Triangle C :

The height of the triangle is 6 \, m.
You need to calculate the unknown width of the triangle. To do this, you need to use the measurements you are given in the question that are parallel to the unknown side:
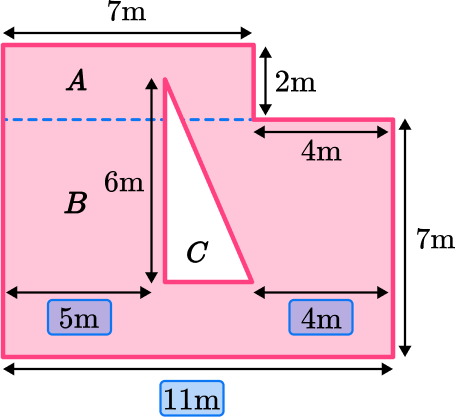
The width of the entire composite shape is 11 \, m. You need to subtract the 5 \, m and 4 \, m from 11 \, m to get the width of shape C.
11-5-4 = 2
\begin{aligned}
\text{ Area }_{C} &=\cfrac{1}{2} \, (\text{ base } \times \text{ height }) \\\\
\text{ Area }_{C} &=\cfrac{2 \, \times \, 6}{2} \\\\
&=6 \, m^{2}
\end{aligned}
Add the areas of the simpler shapes.
\begin{aligned} \text{ Composite Area } &=\text{ Area of } A+\text{ Area of } B-\text{ Area of } C \\\\ &=14+77-6 \\\\ &=85 \end{aligned}
Write down your final answer with square units.
\text { Area }=85 \mathrm{~m}^{2}
Teaching tips for area of composite shapes
- Start with simple shapes like two rectangles before moving onto more complex shapes like triangles and trapezoids.
- Instead of worksheets, offer students a variety of ways to practice finding the area of composite shapes. One idea is for students to create composite shapes (either on paper, using manipulatives, or using an interactive website) and have a partner find the area.
Easy mistakes to make
- Using incorrect units for the answer
A common mistake is to forget to include square units when asked to find area.
- Forgetting to convert measures to a common unit
Before using the formula for calculating the area of a rectangle, you must look at the units given in the question. If different units are given, for example, length = 4 \, m and width = 3 \, cm, you must convert them either both to cm or both to m.
- Trying to figure out a missing side length without calculating
Often, it is possible to reason about the length of a missing side by comparing it to known sides. However, it is important to always use the given sides to calculate the missing side.
For example,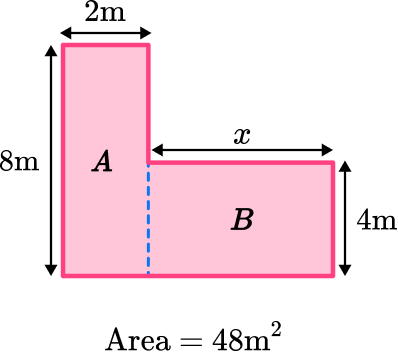
Just by looking, it is pretty obvious the missing side is greater than 2 \, m and 4 \, m. It looks somewhere around 8 \, m. While making observations like this can serve as an estimation strategy – always calculate based on the measurements given to avoid mistakes.
Practice area of composite shapes questions
1. Find the area of the composite shape below:




Split into two rectangles. Find the area of the rectangle and the area of the square and add them together.
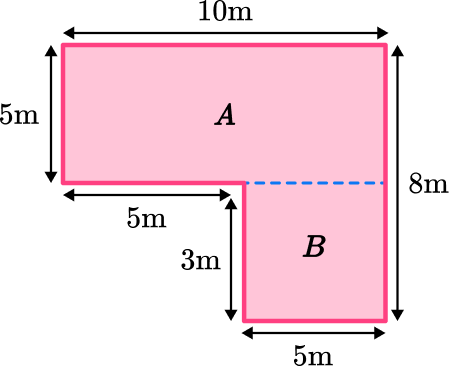
Area of A\text{: } 10 \times 5=50
Area of B\text{: } 5 \times 3=15
Composite Area: 50+15=65 \, m^2
2. Find the area of the composite shape below:
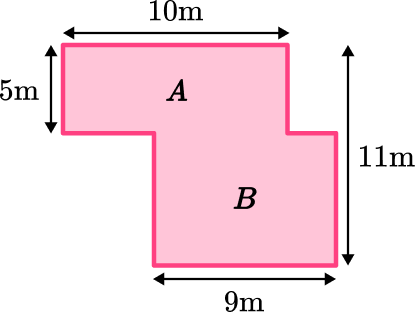




Split into two rectangles. Find the area of the smaller rectangle and the larger rectangle and add them together.
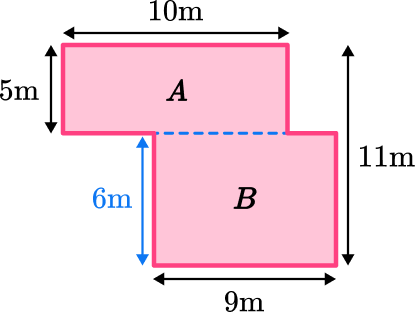
Area of A\text{: } 10 \times 5=50
Area of B\text{: } 9 \times 6=54
Composite Area: 50+54=104 \, m^2
3. The wall shown below needs to be painted. Each tin of paint covers a distance of 4 square meters. How many tins of paint will be needed to cover the entire wall?
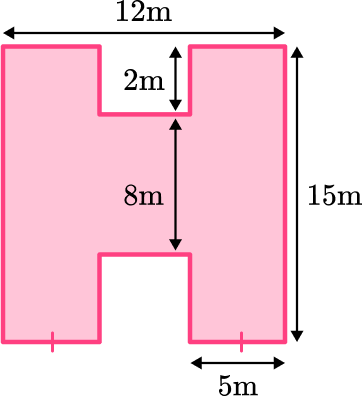




Split into three rectangles:
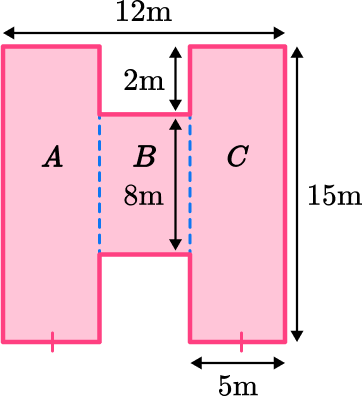
Area of A\text{: } 15 \times 5=75
Area of B\text{: } 8 \times 2=16
Area of C\text{: } 15 \times 5=75
Composite Area: 75+16+75=166 \, m^2
Then divide by 4 to get the number of tins.
166 \, m^2 \div 4=41.5
Since you can’t buy 0.5 of a tin, the answer will be rounded up to 42 tins.
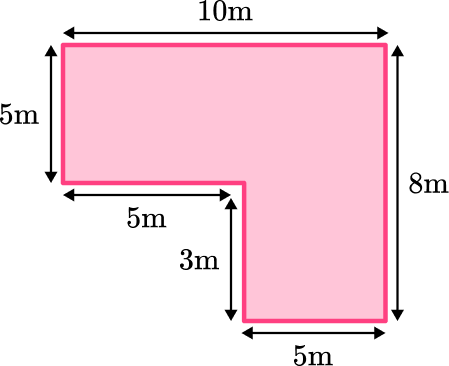
4. Find the area of the composite shape below:
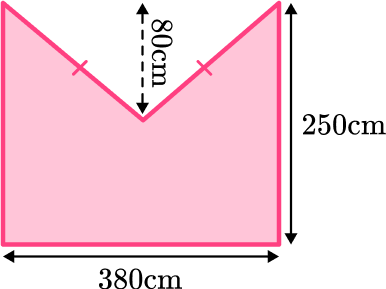




Split into one rectangle and two triangles:
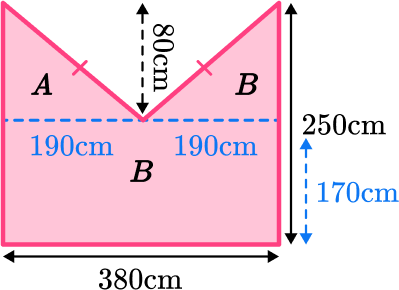
Since you know the triangles are congruent, you can use the base of the rectangle to find the base of the triangles.
380 \mathrm{~cm} \div 2=190 \mathrm{~cm}
Area of A\text{: } \cfrac{1}{2} \, (190 \times 80)=7,600
Area of B\text{: } \cfrac{1}{2} \, (190 \times 80)=7,600
Area of C\text{: } 170 \times 380=64,600
Composite Area: 7,600+7,600+64,6000=79,800 \mathrm{~m}^2
5. Find the value of x in the composite shape below:
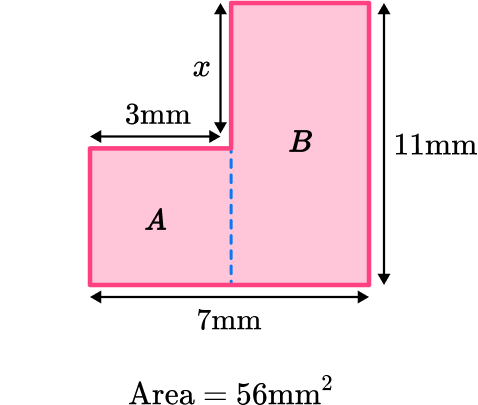




Split into two rectangles:
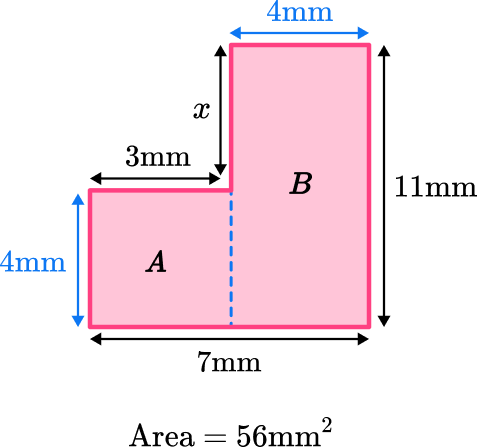
Area of B\text{: } 4 \mathrm{~mm} \times 11 \mathrm{~mm}=44 \mathrm{~mm}^2
The difference between the total area and the area of rectangle B will give you the area of rectangle A\text{:}
56 \mathrm{~mm}^2-44 \mathrm{~mm}^2=12 \mathrm{~mm}^2
The area of rectangle A divide by its width will give you the missing side length:
12 \mathrm{~mm}^2 \div 3 \mathrm{~mm}=4 \mathrm{~mm}
The difference between the length of rectangle B and the length of rectangle A gives you the value of missing side length x.
11 \mathrm{~mm}-4 \mathrm{~mm}=7 \mathrm{~mm}
6. An architect is developing a blueprint for one floor of a house which is shown below. The shaded region represents the floor and will need to be fully tiled. Each square tile has a width of 12 \, cm. How many tiles will be needed to cover the entire floor?
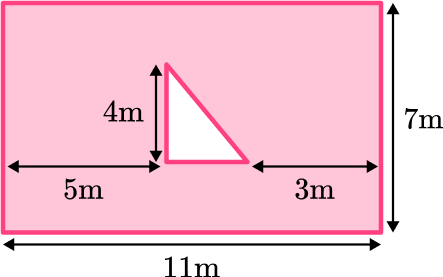




To find the area of the shaded region, you need to first find the total area of the rectangle. Then find the area of the triangle.
Instead of adding the areas together, here you will be subtracting the areas.
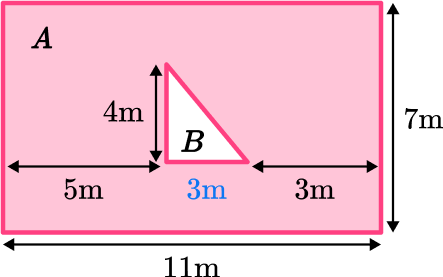
Area of A\text{: } 7 \times 11=77
Area of B\text{: } \cfrac{1}{2} \, (4 \times 3)=6
\begin{aligned} & 77-6=71 \mathrm{~m}^2 \\\\ & 12 \mathrm{~cm}=0.12 \mathrm{~m} \end{aligned}
Area of 1 tile =0.12 \times 0.12=0.0144 \mathrm{~m}^2
71 \div 0.0144=4,930.56 tiles
4,931 tiles
Area of composite shapes FAQs
A composite is a shape composed of basic shapes put together. A composite shape can also be called a compound shape or a composite figure.
To find the area of composite shapes, you must decompose the composite shape into basic shapes, then find the area of each of the basic shapes and add them together.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!