High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Multiplication and division Multiplying and dividing decimals Area of a rectangle Area of a parallelogram Area of a triangleArea of irregular shapes
Here you will learn about the area of irregular shapes, including what irregular shapes are, and questions involving rectilinear shapes, missing side lengths and unit conversion.
Students will first learn about finding the area of an irregular shape as part of geometry in 3 rd grade. Students will deepen their understanding of area of irregular shapes in 4 th grade.
What is the area of irregular shapes?
The area of irregular shapes (also referred to as irregular polygons or irregular figures) is the amount of space inside a shape composed of sides and angles of different lengths and sizes.
It is measured in square units (\mathrm{cm}^{2},\mathrm{~m}^{2},\mathrm{~mm}^{2} etc.).
To find the area of irregular shapes, you will decompose the irregular shape into regular shapes, such as triangles or regular polygons, then find the area of each of the regular shapes and add them together.
Some of the common regular shapes used when decomposing irregular shapes are rectangles, squares, triangles, circles or semicircles, and trapezoids.
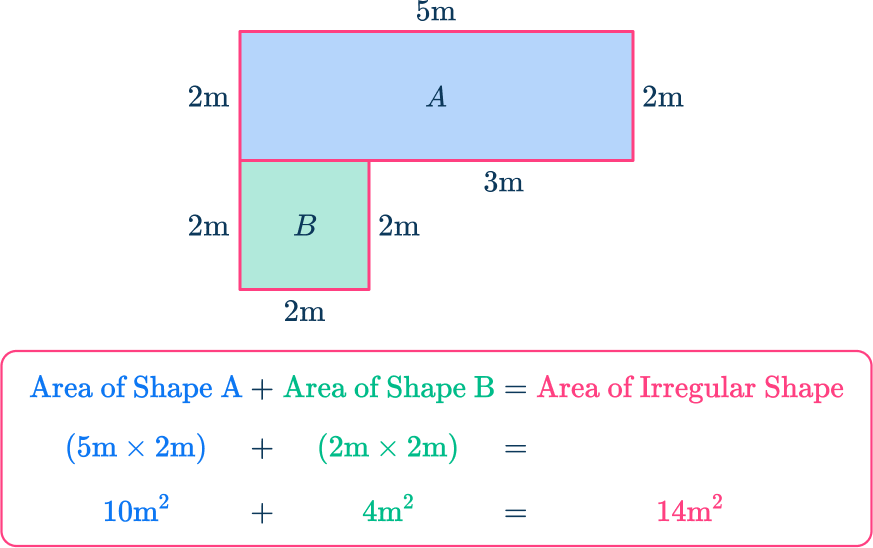
For example,
This irregular shape was split into two shapes, a rectangle (shape A ) and a square (shape B ). Find the area of the rectangle and the area of the square, and then add the two areas together.
![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Check for Understanding Quiz (Grade 4 to 6)
![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 6th and 7th grade area topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Check for Understanding Quiz (Grade 4 to 6)
![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 6th and 7th grade area topics to identify areas of strength and support!
DOWNLOAD FREEArea of irregular shapes using a square grid
Sometimes when finding the area of irregular shapes, they will be presented to you on a square grid. You can find the area of shapes using the square grid by simply counting the squares.
For example, to find the area of the given shape below, you can just count the number of squares, or space, the shape takes up.
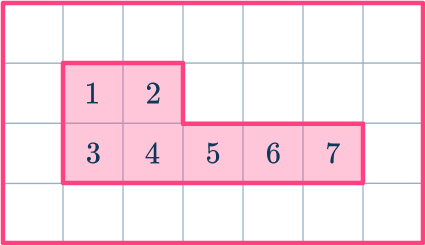
The area of this irregular shape is 7 square units.
What is the area of irregular shapes?

Common Core State Standards
How does this relate to 3 rd grade math and 4 th grade math?
- Grade 3 – Measurement and Data (3.MD.7, 3.MD.7.d)
Relate area to the operations of multiplication and addition; Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.
- Grade 4 – Measurement and Data (4.MD.3)
Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
How to find the area of irregular shapes
In order to find the area of irregular shapes:
- Break down the irregular shape into regular shapes.
- Find the area of each basic shape.
- Add the areas.
- Write down your final answer with square units.
Area of irregular shapes examples
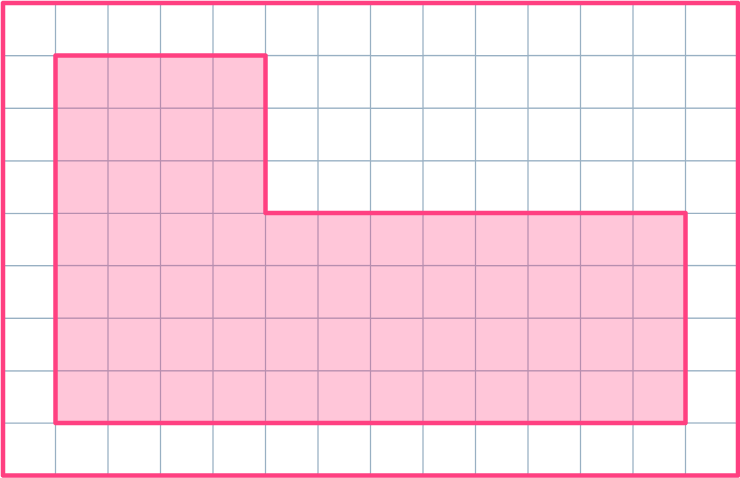
Example 1: using a square grid
Find the area of the given irregular shape.
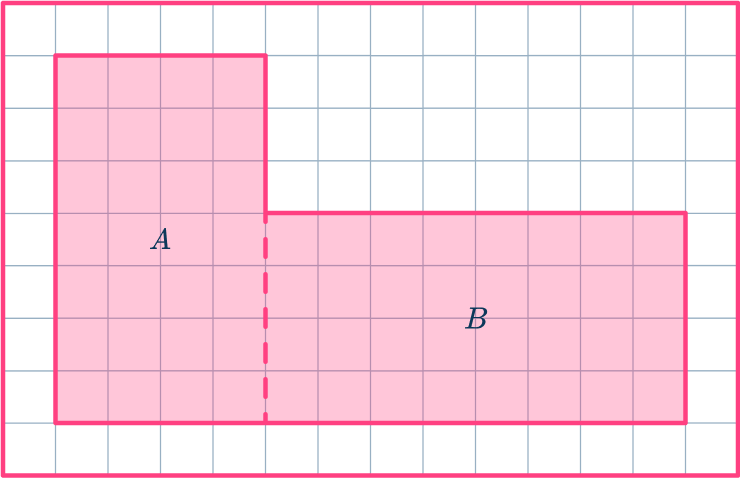
- Break down the irregular shape into regular shapes.
This shape can be broken down into 2 rectangles.
2Find the area of each basic shape.
Find the area of each shape by counting the square units present.
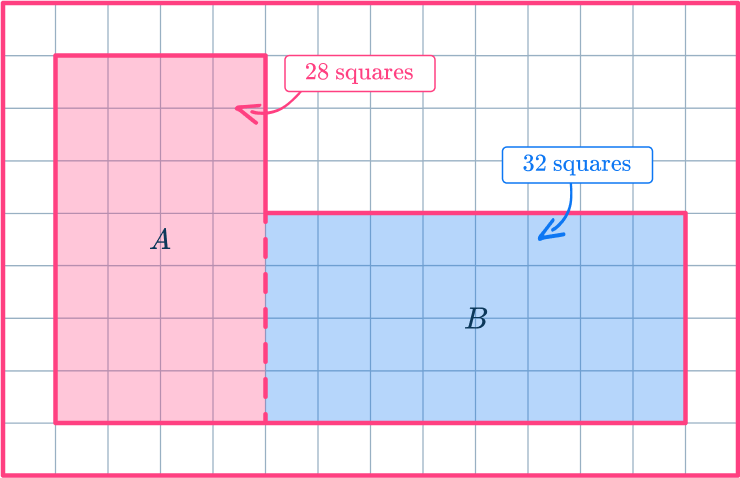
3Add the areas.
\text{Area}=A+B=28+32=604Write down your final answer with square units.
60 square units.
Example 2: using a square grid
Find the area of the given irregular shape.
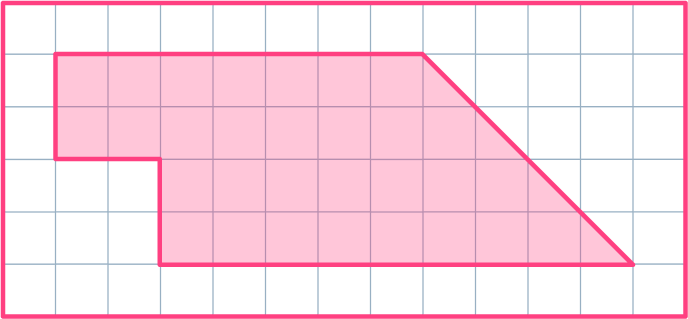
Break down the irregular shape into regular shapes.
This shape can be broken down into three smaller shapes, a square, a rectangle, and a triangle.
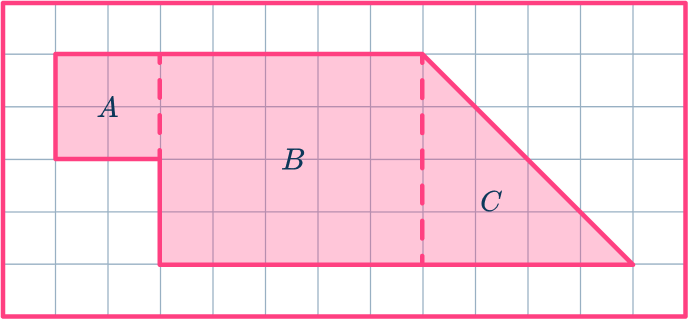
Find the area of each basic shape.
Find the area of each shape by counting the square units present. Remember that two half squares make 1 square.
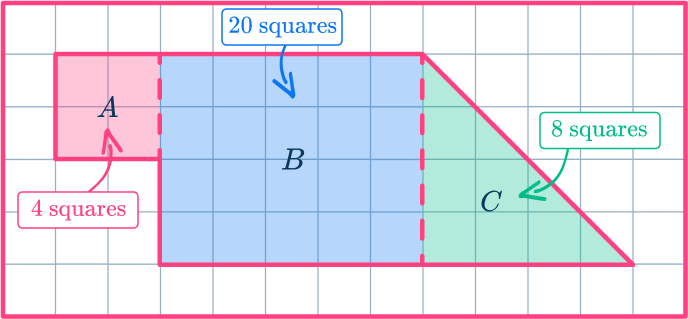
Add the areas.
Write down your final answer with square units.
32 square units.
Example 3: word problem
Bridges High School is putting in a flower bed in the courtyard. The sketch below shows the flower bed in square feet. What is the area of the new flower bed?
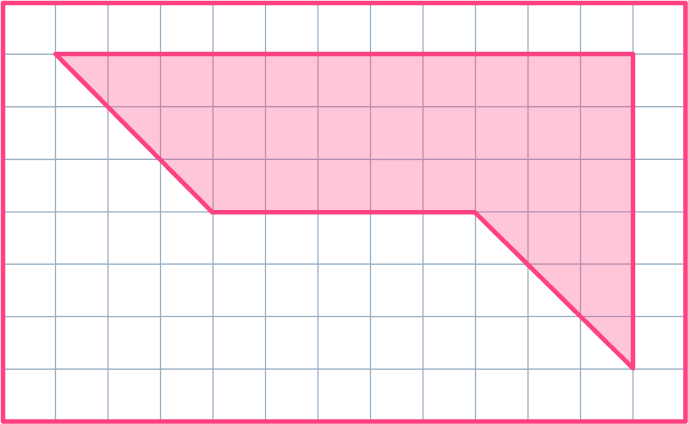
Break down the irregular shape into regular shapes.
This shape can be broken down into three shapes, two triangles and one rectangle.
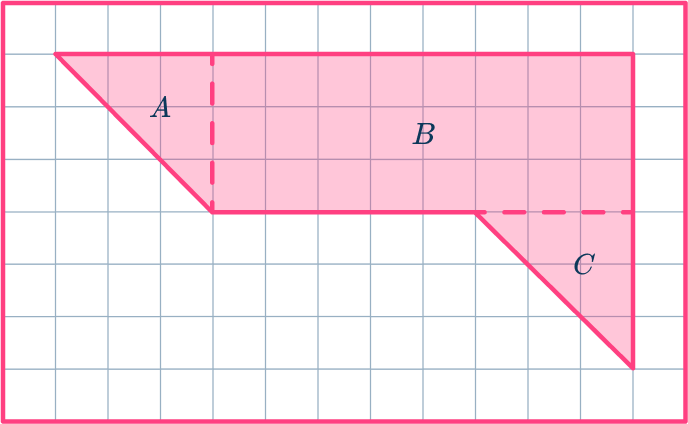
Find the area of each basic shape.
Find the area of each shape by counting the square units present.
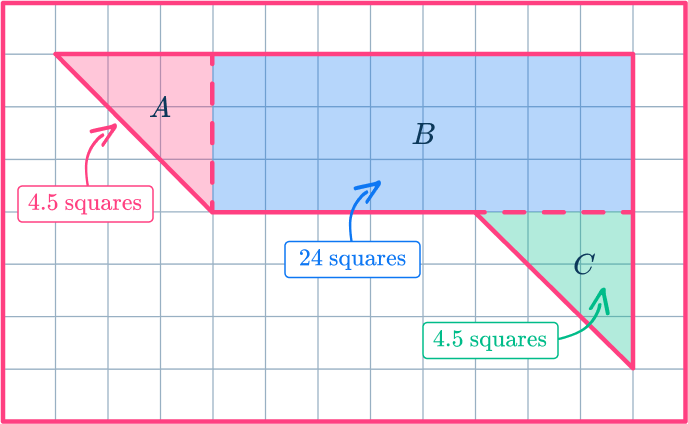
Add the areas.
Write down your final answer with square units.
Example 4: irregular shapes (all sides given)
Find the area of the irregular shape below.
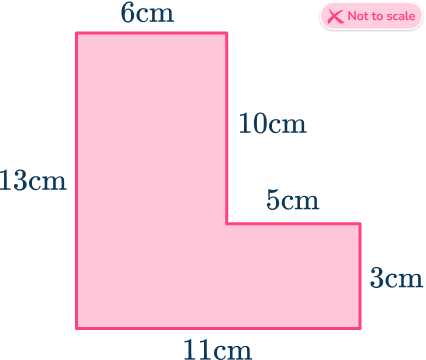
Break down the irregular shape into regular shapes.
We can split the shape into 2 rectangles.
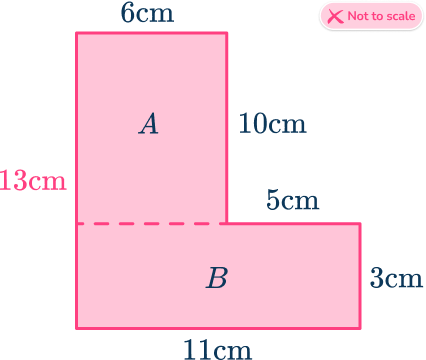
The length of 13 \, cm is no longer correct as it has been split into two separate lengths, matching the vertical faces on the opposite side of the rectangles
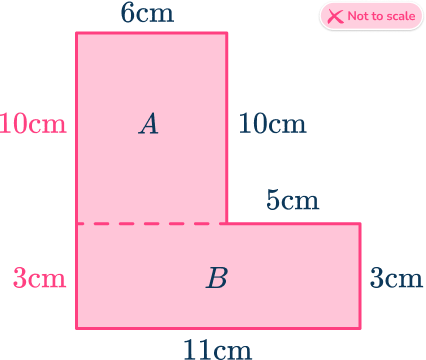
Find the area of each basic shape.
Use the formula for finding the area of a rectangle: A=l \times w
The area of A is: A=l\times{w}=10\times{6}=60
The area of B is: A=l\times{w}=11\times{3}=33
Add the areas.
Write down your final answer with square units.
Example 5: irregular shapes (missing sides)
Find the area of the irregular shape below.
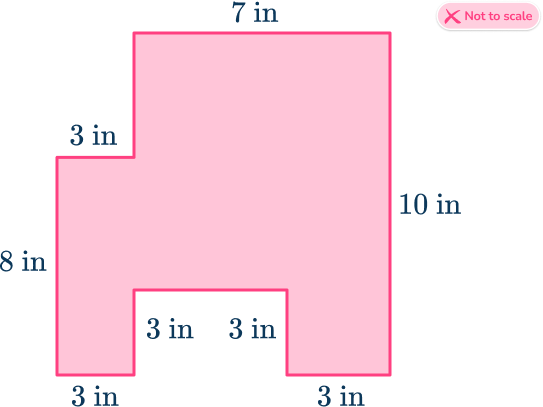
Break down the irregular shape into regular shapes.
This shape can be broken down into 4 smaller shapes, 2 squares and 2 rectangles.
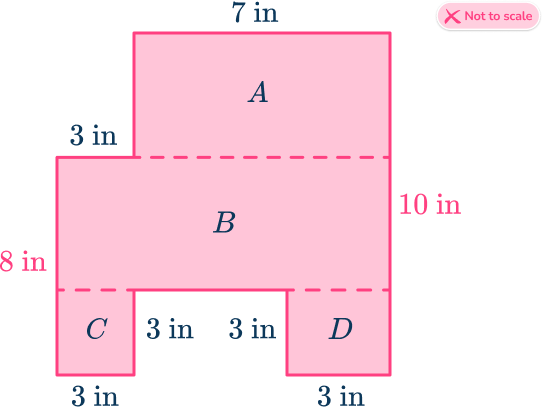
The two vertical lengths of 8\mathrm{~in} and 10\mathrm{~in} must change as these lengths have been split up.
First, the height of A must be 2\mathrm{~in} as the vertical edges sum to 10\mathrm{~in} \, (10-8=2).
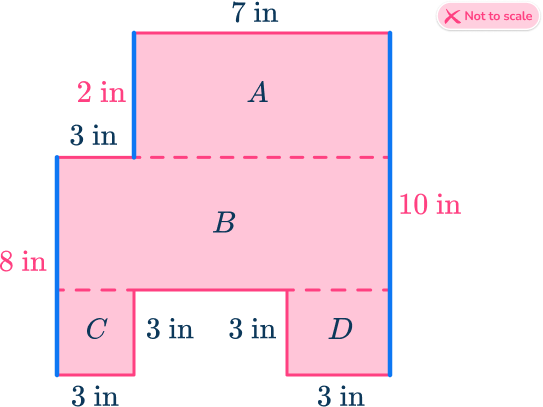
As the height of C is 3\mathrm{~in}, the height of B is 5\mathrm{~in} \, (8-3=5).
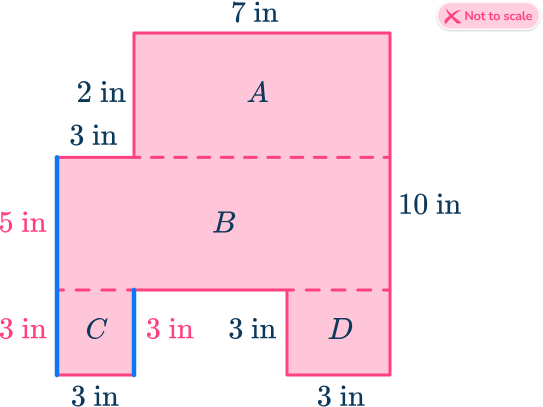
Next, relabel the vertical side of 10\mathrm{~in} into the three component lengths: 2\mathrm{~in},~5\mathrm{~in},~3\mathrm{~in}.
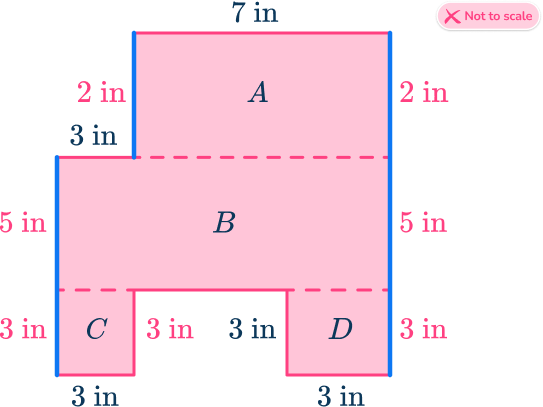
Finally, calculate the width of B using the horizontal components (7+3=10).
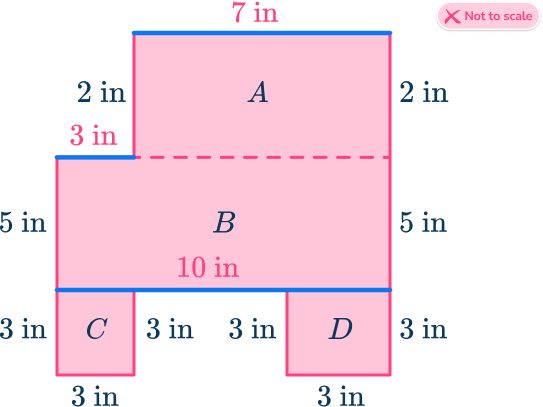
Find the area of the basic shapes.
Add the areas.
Write down your final answer with square units.
Example 6: word problem
Emma built a dog run that has two dog lanes and space in the middle for a water area. She divided the dog run as seen below. The shape has a horizontal and vertical line of symmetry. What is the total area of her new dog run?
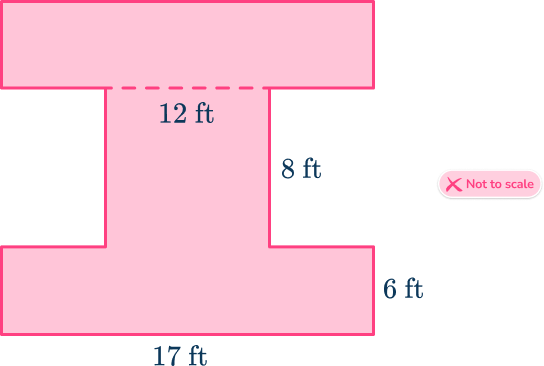
Break down the irregular shape into regular shapes.
As the shape has a horizontal and vertical line of symmetry, label the sides that do not require calculation:
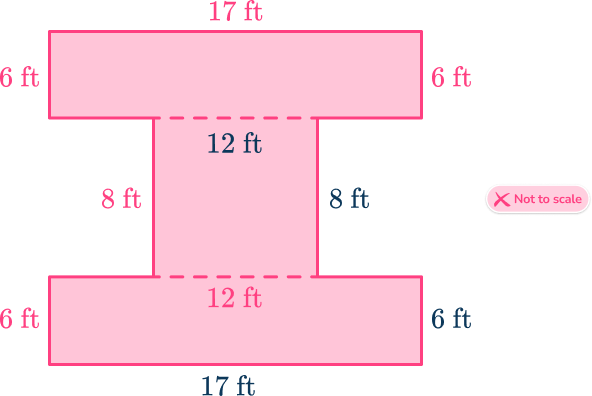
The missing horizontal lengths are:
(17-12)\div{2}=2.5\mathrm{~ft}.
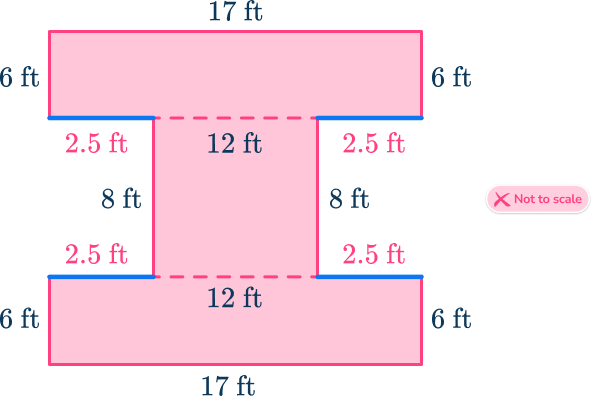
Label each of the three rectangles:
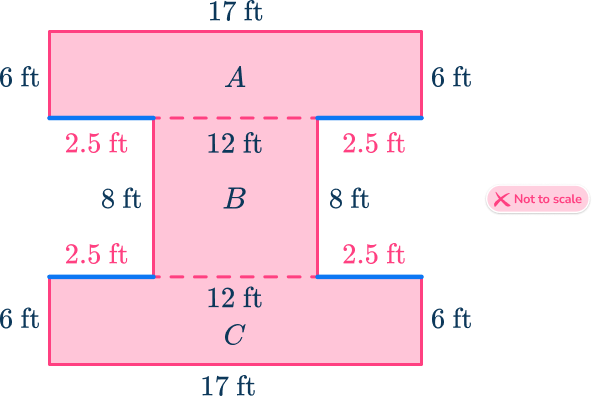
Find the area of the basic shapes.
Add the areas.
Write down your final answer with square units.
Teaching tips for area of irregular shapes
- While area of irregular shapes worksheets are necessary to allow for student practice, providing students with visual aids, such as grid paper and colored shapes, can help students visualize the decomposition of irregular shapes into regular shapes.
- When creating lesson plans, make sure to incorporate the many different technology tools that exist that can help students find the area of irregular shapes.
- Have students work collaboratively to create study materials, such as a step-by-step guide or examples that have been solved. These can assist students by giving them something to study outside of the classroom, and refer back to as often as needed.
Easy mistakes to make
- Miscounting squares when using a square grid
Take care when counting squares using a square grid. Find a way to mark each square so you don’t end up counting the same square more than once, or forgetting a square all together. It’s also important to note any partial squares that can be added as fractions.
- Using the wrong formulas when calculating area
Label each type of basic or regular shape based on its properties. It’s important to be familiar with how to find the area of each of these shapes, including the area of the triangle.
- Forgetting to add up all individual shapes
Labeling each individual shape with a letter or number can help ensure that you do not forget a shape when calculating the total area.
Writing an equation with each of the shapes ( for example, \text{Area}=A+B+C) before starting any math calculations can help make sure you account for each area.
Practice area of irregular shapes questions
1. Find the area of the irregular shape.
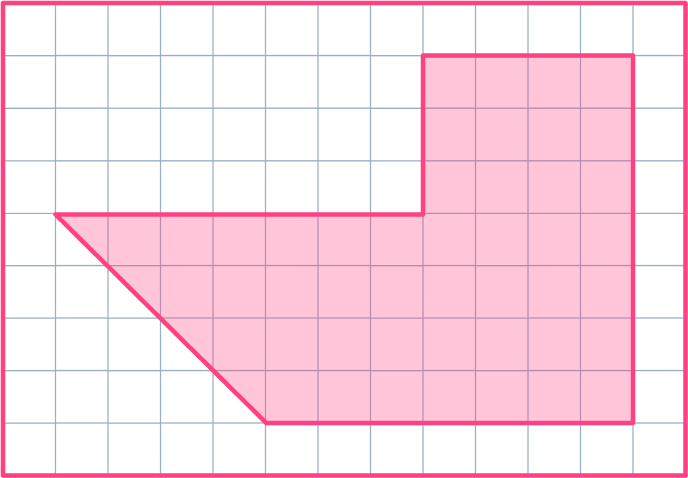
28 square units

48 square units

20 square units

52 square units

Split the irregular shape into smaller, regular shapes, and then count the squares within the shape to find the area.
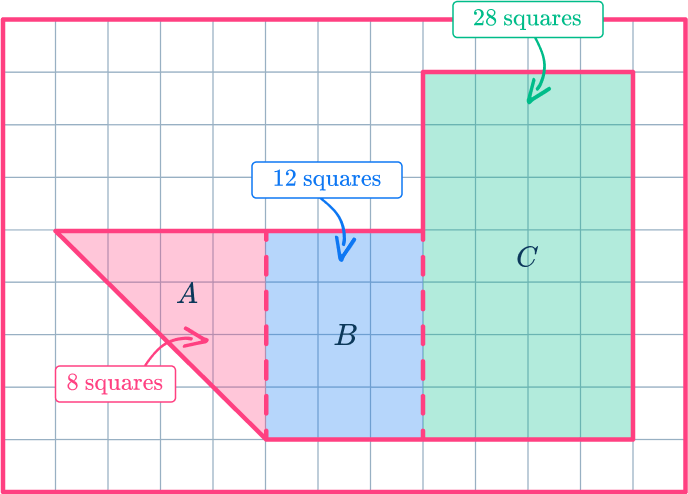
8+12+28=48 square units
2. Find the area of the irregular shape.

144 square units

48 square units

80 square units

96 square units

Split the irregular shape into smaller, regular shapes, and then count the squares within the shape to find the area.
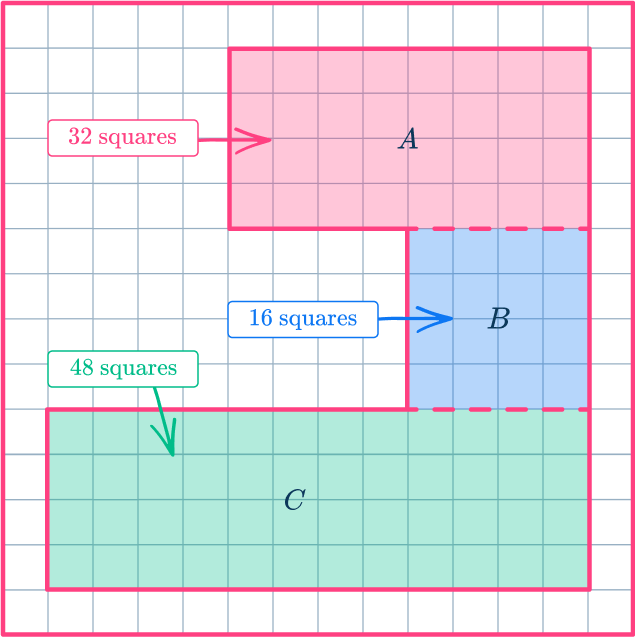
32+16+48=96 square units
3. Find the area of the irregular shape.
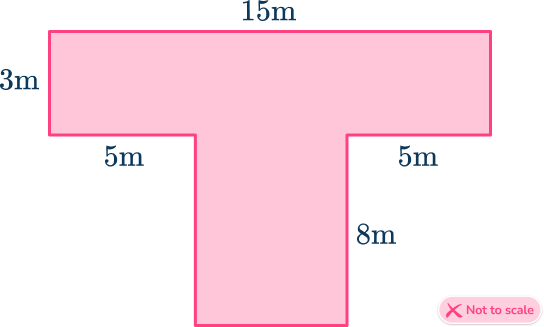
40 square meters

77 square meters

45 square meters

85 square meters

Divide the shape into 2 rectangles, and find the area of each rectangle.
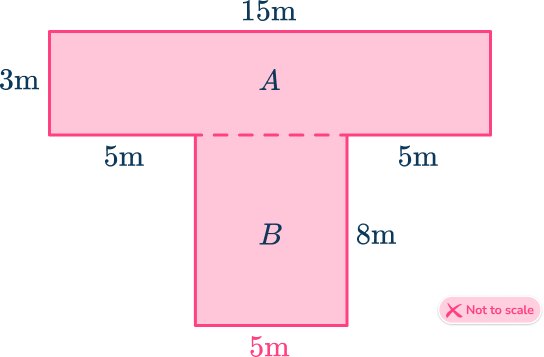
A=3\times{15}=45
B=5\times{8}=40
\text{Area}=45+40=85\mathrm{~m}^2
4. The irregular shape below has one horizontal line of symmetry.
Find the area of the irregular shape.
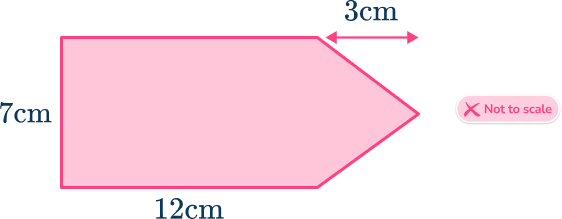




Divide the shape into a rectangle and a triangle, then use the appropriate formulas to find the area of both shapes.
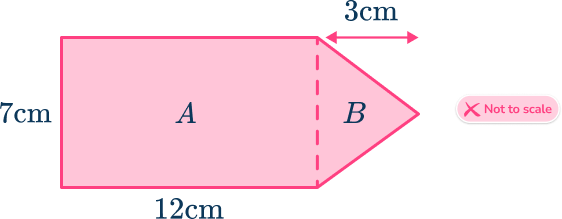
A=7\times{12}=84
B=(3\times{7})\div{2}=10.5
84+10.5=94.5\mathrm{~cm}^2
5. Kimberly is replacing the flooring in 3 of the rooms in her house and the hallway between them. The plan of the rooms has a horizontal and vertical line of symmetry.
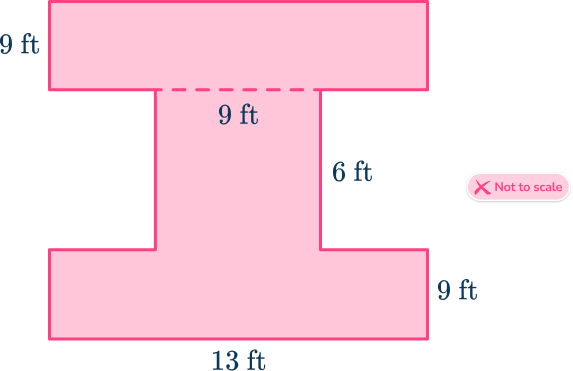
What is the total area of flooring that Kimberly will replace?




Divide the areas into 3 rectangles and find the area of each. As the shape has two lines of symmetry, write the missing side lengths, including any calculated length.
(13-9)\div{2}=2\mathrm{~ft}
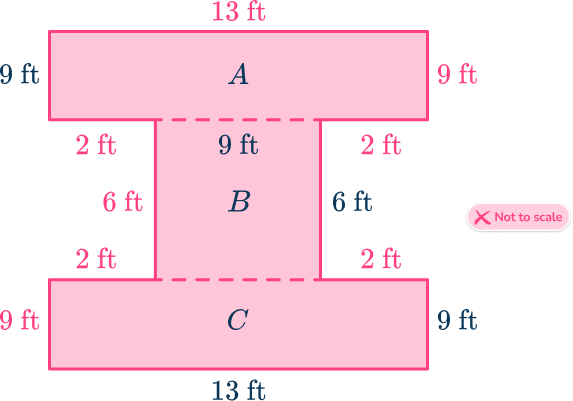
A=13\times{9}=117
B=9\times{6}=54
C=13\times{9}=117
\text{Area}=117+54+117=288\mathrm{~ft}^2
6. A city park has an irregular shape that is divided into three sections: a rectangular playground, a triangular garden and a square picnic area.
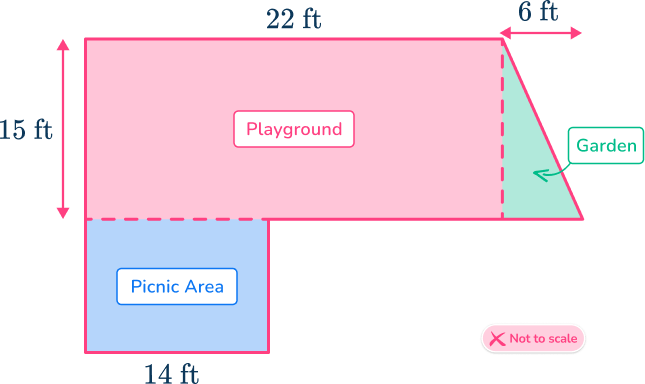
What is the total area of the city park?




Find the area of the three regular shaped areas to find the total area of the irregular shape.
Playground:
\text{Area}=l\times{w}=22\times{15}=330
Picnic Area:
\text{Area}=l\times{l}=14\times{14}=196
Garden:
\text{Area}=\cfrac{1}{2}\times{b}\times{h}=\cfrac{1}{2}\times{6}\times{15}=45
\begin{aligned}\text{Total area}&=\text{Playground}+\text{Picnic area}+\text{Garden} \\\\ &=330+196+45 \\\\ &=571\mathrm{~ft}^2 \end{aligned}
Area of irregular shapes FAQs
An irregular shape is any shape that does not have equal sides or angles. These shapes cannot be classified by any standard geometric names, like squares or triangles. Some examples of irregular shapes include polygons with different side lengths and shapes with curved boundaries.
You can find the area of composite figures, or shapes, similarly to how you find the area of irregular shapes. You can break the composite shape into basic shapes, find the area of each individual shape, and then add the sums together to find the total area of the composite shape.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!