[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!!
Area of a square
Here you will learn about finding the area of a square, including counting units squares and multiplying the side lengths.
Students will first learn about the area of a square as part of measurement and data in 3 rd grade.
What is the area of a square?
The area of a square is the amount of space inside the square. It is measured in square units.
For example,
The square units line up with all sides of the square and do not overlap. The area of the square is the number of square units within it.
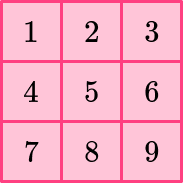
Notice the connection between the side of a square and the square units:
The side length is always the same as the number of columns and rows of square units, since a square has equal sides.
This is why the area of square formula is \text {side} \times \text {side.}
For example,
Area is always labeled in square units. You can write it out or use the exponent 2 (a small 2 ) to show the units are square.
For example,
square centimeters (\mathrm{cm}^2), square meters (\mathrm{m}^2), square feet (\mathrm{ft}^2), square inches (\mathrm{in}^2).
The area of other polygons is also measured in square units.
For example,
The square units of the rectangle line up with the sides, just like they did for the square. There are 27 square units inside the rectangle, so that is the area.
Notice that this is not true for the other shapes. Some or all of their sides do not line up with the square units. Counting their square units is not as easy. This is why the area of a circle, triangle, hexagon and other shapes is covered in later grades.
What is the area of a square?
Common Core State Standards
How does this relate to 3 rd grade math and 4 th grade math?
- Grade 3 – Measurement and Data (3.MD.C.5)
Recognize area as an attribute of plane figures and understand concepts of area measurement.
a. A square with side length 1 unit, called “a unit square,” is said to have “one square unit” of area, and can be used to measure area.
b. A plane figure which can be covered without gaps or overlaps by n unit squares is said to have an area of n square units.
- Grade 3 – Measurement and Data (3.MD.C.6)
Measure areas by counting unit squares (square cm, square m, square in, square ft, and improvised units).
- Grade 3 – Measurement and Data (3.MD.C.7a)
Find the area of a rectangle with whole-number side lengths by tiling it, and show that the area is the same as would be found by multiplying the side lengths.
How to find the area of a square
In order to find the area of a square by counting unit squares:
- Be sure that the square is made of whole unit squares in an array.
- Count the unit squares to find the area.
In order to calculate the area of a square:
- Identify the side length of the square.
- Write down the formula for the area of a square.
- Substitute the given values and calculate.
- Write down your final answer with units squared.
![[FREE] End of Year Math Assessments (Grade 4 & Grade 5)](https://thirdspacelearning.com/wp-content/uploads/2023/02/end-of-year-math-assessment-grade-4-grade-5.png)
[FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREE [FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREEArea of a square examples
Example 1: counting unit squares to find the area
What is the area of the square?
- Be sure that the square is made of whole unit squares in an array.
The unit squares inside the square line up with the sides of the square.
2Count the unit squares to find the area.
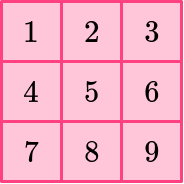
The area of the square is 9 square units.
Example 2: counting unit squares to find the area
What is the area of the square?
Be sure that the square is made of whole unit squares in an array.
The unit squares inside the square line up with the sides of the square.
Count the unit squares to find the area.
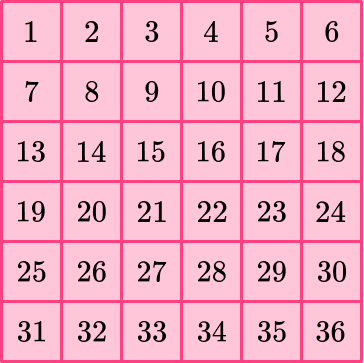
The area of the square is 36 square units.
Example 3: counting unit squares (and multiplying the sides) to find the area
What is the area of the square?
Identify the side length of the square.
Write down the formula for the area of a square.
Since the length of its sides is 7, the unit squares form a 7 by 7 array.
To find the total number of unit squares (the area) multiply: \text {side} \times \text {side. }
Substitute the given values and calculate.
\text { Area }=7 \times 7=49
You can prove this by counting the unit squares within.
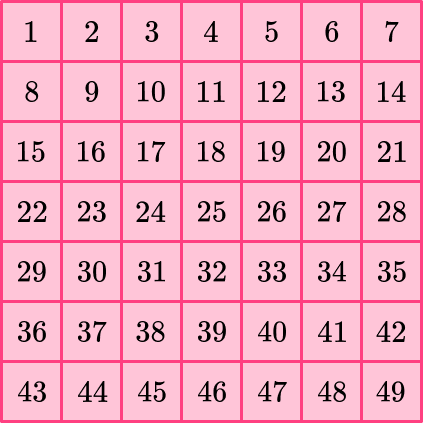
Write down your final answer with units squared.
The area of the square is 49 square units.
Example 4: counting unit squares (and multiplying the sides) to find the area
What is the area of the square?
Identify the side length of the square.
Write down the formula for the area of a square.
Since the length of each side is 5, the unit squares form a 5 by 5 array.
To find the total number of unit squares (the area) multiply: \text {side} \times \text {side.}
Substitute the given values and calculate.
\text { Area }=5 \times 5=25
You can prove this by counting the unit squares within.
Write down your final answer with units squared.
The area of the square is 25 square units.
Example 5: multiplying the sides to calculate the area
What is the area of the square?
Identify the side length of the square.
Since the length of the sides is the same, all sides are 8 \, cm.
Write down the formula for the area of a square.
\text { Area of a square }=\text { side } \times \text { side }
Substitute the given values and calculate.
\text { Area of a square }=8 \times 8=64
Write down your final answer with units squared.
The area of the square is 64 square centimeters.
Example 6: multiplying the sides to calculate the area
The wall above needs to be painted. How many square feet of paint is needed to cover the wall?
Identify the side length of the square.
Since the length of a side is the same as the others, all sides are 4 \, ft.
Write down the formula for the area of a square.
\text { Area of a square }=\text { side } \times \text { side }
Substitute the given values and calculate.
\text { Area of a square }=4 \times 4=16
Write down your final answer with units squared.
The wall needs 16 square feet of paint to cover it.
Teaching tips for area of a square
- Make sure students have plenty of practice with tiling squares to find the area (via manipulatives or a digital resource that allows them to do this). These opportunities can provide the conceptual understanding necessary to use the area formula.
- Worksheets can be a great source for practice, but be sure to use worksheets that provide a variety of practice (squares whose area can be found by using physical tiles and squares with or without grids).
Easy mistakes to make
- Confusing area and perimeter of a square
When first learning about these two concepts, it can be easy to confuse them. Remember that perimeter is the distance around a square and can be found by adding all the sides up (or multiplying one side by 4 ) and area is the space within the square and can be found by multiplying two sides or counting the unit squares within.
For example,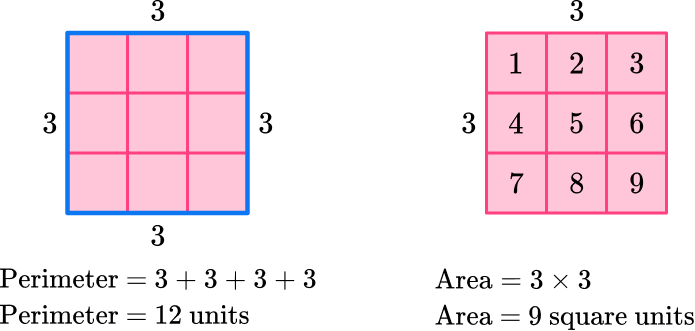
- Not using common units
When tiling a shape to find the area, it is important that all the tiles are the same size. When solving area problems with real world measurements, it is important that all measurements are in the same unit. Having different size tiles or measurements will make the area calculation incorrect.
Related area lessons
- Area
- Area of a quadrilateral
- Area of a rectangle
- Area of a parallelogram
- Area of a trapezoid
- Area of a rhombus
- Area of a triangle
- Area of a right triangle
- Area of an isosceles triangle
- Area of an equilateral triangle
- Area of an obtuse triangle
- Area of composite shapes
- Area of rectilinear figures
Practice area of square questions
1. What is the area of the square?
4 square units
8 square units
12 square units
16 square units
The unit squares inside the square line up with the sides of the square and form an array.
Count the unit squares to find the area.
The area of the square is 16 square units.
2. Which square has an area of 25 square units?
Count the unit squares to find the area.
The area of the square is 25 square units.
The area can also be found by multiplying \text {side} \times \text {side. } Since 5 \times 5=25, a square with the area of 25 square units will have side lengths of 5.
3. What is the area of the square?
6 square units
24 square units
30 square units
36 square units
Since the length of its sides is 6, the unit squares form a 6 by 6 array.
To find the total number of unit squares (the area) multiply: \text { side} \times \text {side.}
\text { Area }=6 \times 6=36
You can prove this by counting the unit squares within.
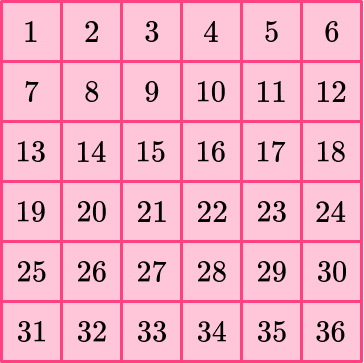
The area of the square is 36 square units.
4. What is the area of the square?
77 square units
64 square units
16 square units
32 square units
Since the length of its sides is 8, the unit squares form an 8 by 8 array.
To find the total number of unit squares (the area) multiply: \text { side} \times \text {side.}
\text { Area }=8 \times 8=64
You can prove this by counting the unit squares within.
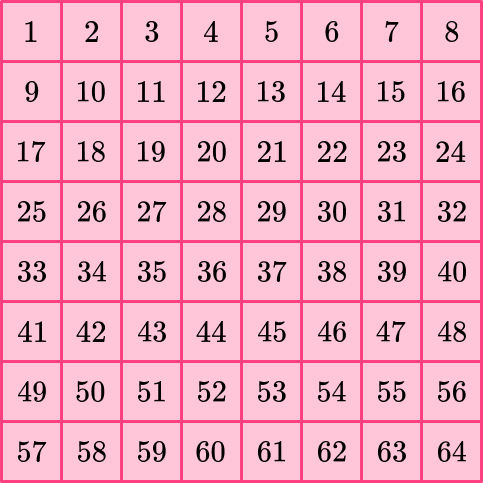
The area of the square is 64 square units.
5. What is the area of the square?
81 square feet
9 square feet
18 square feet
36 square feet
\begin{aligned}\text { Area of a square } & =\text { side } \times \text { side } \\\\ & =9 \times 9 \\\\ & =81\end{aligned}
The area of the square is 81 square feet.
6. The area of a square is 4 square inches. What is the side length of the square?
1 inch
2 inches
4 inches
16 inches
\begin{aligned}\text { Area of a square } &=\text { side } \times \text { side } \\\\ 4 &=\text { side } \times \text { side }\end{aligned}
Think about a number times itself that equals 4…
Since 2 \times 2=4, the square has a side length of 2 inches.
Area of a square FAQs
To calculate the area of a square that has fractional side lengths, you still multiply \text {side} \times \text {side,} so you can either use a calculator or use what you know about multiplying fractions to solve.
Both the area and the perimeter are calculated using the side lengths, but they are not calculated in the same way. The formula for perimeter of a square is 4 \times \text {side length} and the formula for area is \text {side length} \times \text {side length.}
Surface area is the area of the faces of 3D figures. It is found by calculating the area of each side of a shape and then adding them all together.
See also: Surface area
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.