[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
2D shapes Polygons Parallel lines Types of anglesQuadrilaterals
Here you will learn about quadrilaterals, including their names, attributes and how to classify them.
Students first learn about quadrilaterals in early elementary school with their work in geometry. They expand upon the types of quadrilaterals as they progress through elementary school.
What are quadrilaterals?
Quadrilaterals are polygons with four straight sides, four angles, and four vertices.
Here are the special types of quadrilaterals.
| Name | Shape | Attributes |
|---|---|---|
| Square |  | ● Four right angles |
| Rectangle | 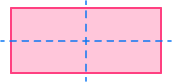 | ● Two pairs of opposite congruent sides |
| Parallelogram |  | ● Two pairs of opposite congruent sides |
| Rhombus |  | ● Four congruent sides |
| Trapezoid |  | ● One pair of opposite parallel sides called bases |
| Isosceles Trapezoid |  | ● Non-parallel sides are congruent |
| Kite |  | ● Two pairs of adjacent sides that are congruent (next to each other) |
To help remember the properties of quadrilaterals and how they relate to one another. You can use a Venn diagram.
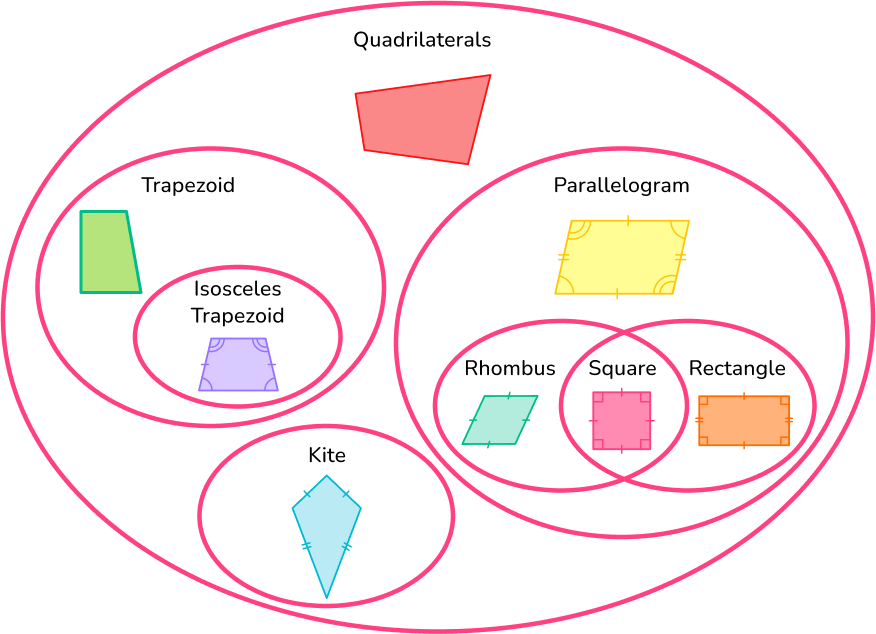
Step-by-step guide: Types of Quadrilaterals
Diagonals:
Quadrilaterals have two diagonals. Diagonals are line segments that connect non-consecutive vertices.

Other properties of quadrilaterals:
- The sum of the interior angles of a quadrilateral total 360 ^{\circ}.
- Quadrilaterals can be convex or concave.
⟶ A convex quadrilateral is a polygon with all interior angles less than 180^{\circ}. All quadrilaterals shown in the table above are convex.
⟶ A concave quadrilateral has at least one angle that is greater than 180^{\circ} (or a reflex angle). The quadrilateral shown below is concave.

What are quadrilaterals?
![[FREE] Quadrilateral Worksheet (Grade 2 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Quadrilateral-listing-image.png)
[FREE] Quadrilateral Worksheet (Grade 2 to 5)
![[FREE] Quadrilateral Worksheet (Grade 2 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Quadrilateral-listing-image.png)
Use this quiz to check your grade 2 to 5 students’ understanding of Quadrilaterals. 15+ questions with answers covering a range of 2nd, 3rd, 4th, and 5th grade quadrilateral topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Quadrilateral Worksheet (Grade 2 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Quadrilateral-listing-image.png)
[FREE] Quadrilateral Worksheet (Grade 2 to 5)
![[FREE] Quadrilateral Worksheet (Grade 2 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Quadrilateral-listing-image.png)
Use this quiz to check your grade 2 to 5 students’ understanding of Quadrilaterals. 15+ questions with answers covering a range of 2nd, 3rd, 4th, and 5th grade quadrilateral topics to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 2 nd grade – 5 th grade math?
- Grade 2 – Geometry (2.G.A.1)
Recognize and draw shapes having specified attributes, such as a given number of angles or a given number of equal faces. Identify triangles, quadrilaterals, pentagons, hexagons, and cubes.
- Grade 3 – Geometry (3.G.A.1)
Understand that shapes in different categories (example, rhombuses, rectangles, and others) may share attributes (example, having four sides), and that the shared attributes can define a larger category (example, quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories.
- Grade 4 – Geometry (4.G.A.2)
Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Recognize right triangles as a category, and identify right triangles.
- Grade 5 – Geometry (5.G.3)
Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category. For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles.
- Grade 5 – Geometry (5.G.4)
Classify two-dimensional figures in a hierarchy based on properties.
How to name quadrilaterals
In order to name a quadrilateral:
- Examine the properties of the quadrilateral, including side and angle relationships.
- Identify the quadrilateral.
Quadrilaterals examples
Example 1: parallelogram
The quadrilateral has two pairs of parallel sides. Identify the type of quadrilateral that it is.

- Examine the properties of the quadrilateral, including side and angle relationships.
The quadrilateral has two pairs of parallel sides. It also appears that the quadrilateral has two pairs of opposite congruent sides and two pairs of opposite congruent angles.

2Identify the quadrilateral.
The quadrilateral is a parallelogram.
Example 2: rectangle
What is the best classification for the quadrilateral?

Examine the properties of the quadrilateral, including side and angle relationships.
The sides of the quadrilateral are not all equal. The quadrilateral has two pairs of opposite congruent sides, two pairs of opposite parallel sides, and four equal angles – right angles.
Identify the quadrilateral.
The best classification for the quadrilateral is a rectangle. Rectangles are special types of parallelograms.
Example 3: regular quadrilateral
Select the regular quadrilateral and name it.

Examine the properties of the quadrilateral, including side and angle relationships.
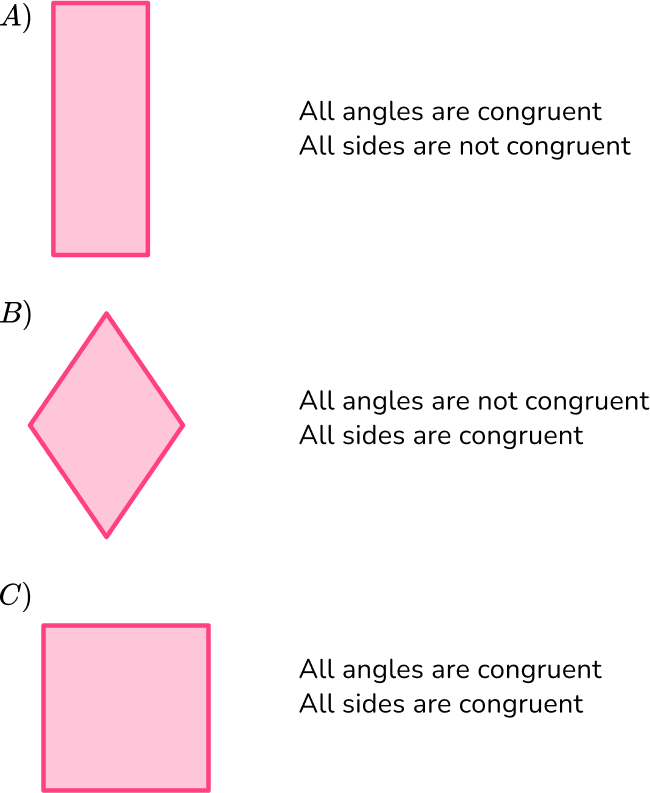
Identify the quadrilateral.
Choice C is the regular quadrilateral because all of the sides are congruent and all angles are congruent. The regular quadrilateral is a square.
Example 4: rhombus
Kelly wants to classify the quadrilateral. What is the best classification?
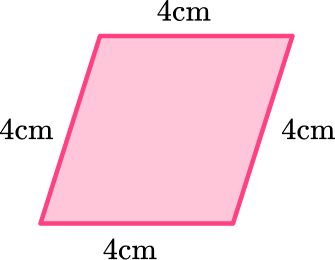
Examine the properties of the quadrilateral, including side and angle relationships.
The quadrilateral has two pairs of parallel sides as well as all four congruent sides. All four angles are not congruent.
Identify the quadrilateral.
The quadrilateral is a rhombus. Rhombuses are special types of parallelograms.
Example 5: trapezoid
Name the quadrilateral.

Examine the properties of the quadrilateral, including side and angle relationships.
The quadrilateral has one pair of opposite sides that are parallel.
Identify the quadrilateral.
The quadrilateral is a trapezoid.
Example 6: quadrilaterals
Describe how the quadrilaterals are the same and how they are different. Name them.

Examine the properties of the quadrilateral, including side and angle relationships.
Quadrilateral A has two pairs of opposite parallel sides and two pairs of opposite congruent sides. Quadrilateral A also has two pairs of opposite congruent angles.
Quadrilateral B has one pair of opposite parallel sides and two pairs of congruent angles. Quadrilateral B also has one pair of opposite congruent sides.
The quadrilaterals are the same because they have a pair of opposite parallel sides, a pair of opposite congruent sides, and two pairs of congruent angles.
They are different because Quadrilateral A has two pairs of opposite parallel sides and Quadrilateral B only has one pair.
Quadrilateral A has two pairs of opposite congruent sides, and quadrilateral B only has one. Also, Quadrilateral A has two pairs of opposite angles that are congruent, whereas Quadrilateral B has adjacent angles (next to each other) that are congruent.

Identify the quadrilateral.
Quadrilateral A is a parallelogram.
Quadrilateral B is an isosceles trapezoid.
Teaching tips for quadrilaterals
- Have students create a hierarchy of quadrilaterals on their own so that they can investigate the relationships between the sides of a quadrilateral and the angles of a quadrilateral.
- Instead of worksheets, have students engage with geometric digital platforms such as desmos to investigate the properties of quadrilaterals.
- Incorporate project based learning activities which include ways for students to see how the concepts are applied in a real world setting.
Easy mistakes to make
- Assuming all quadrilaterals with four \bf{90}^{\circ} angles are squares
Rectangles and squares are quadrilaterals with four right angles. If the four sides are equal, then it is a square. If the four sides are not equal, then it is a rectangle.
- Mistaking a trapezoid for a parallelogram
Trapezoids are not classified as parallelograms because they do not hold the properties of parallelograms. Trapezoids have only one pair of opposite parallel sides. Parallelograms have two pairs of opposite parallel sides.
- Mistaking a rhombus for a square
A rhombus has four equal sides, but its angles are not right angles like in a square.
Practice quadrilateral questions
1. Identify the quadrilateral.

rectangle

trapezoid

square

rhombus

The quadrilateral has four congruent sides and the four angles are not congruent. So, the quadrilateral is a rhombus.
2. Which quadrilateral has two pairs of opposite parallel sides and four right angles, but does NOT have all sides of equal length?
Rhombus

Rectangle

Parallelogram

Square

Quadrilaterals with two pairs of opposite parallel sides with four right angles have to be a special parallelogram, which is either a rectangle or a rhombus. Since the quadrilateral does not have four congruent sides, it must be a rectangle.
3. Which quadrilateral is NOT a parallelogram?








The only quadrilateral that cannot be a parallelogram from the choices is the trapezoid.

A trapezoid has only one pair of opposite parallel sides whereas parallelograms have two pairs of opposite parallel sides.
4. Which statement is true?
A square is always a rhombus.

A rhombus is always a square.

A trapezoid is always a parallelogram.

A parallelogram is always a trapezoid.

A square is always considered a rhombus because, in order for a quadrilateral to be a rhombus, it has to have 4 congruent sides. Squares have four congruent sides.
However, a rhombus is not always a square because in order for a quadrilateral to be a square it has to have four congruent sides and four right angles. Rhombuses do not have four right angles.
5. Which quadrilateral could have side lengths 10 \, cm, 6 \, cm, 10 \, cm, 6 \, cm?
Rhombus

Parallelogram

Trapezoid

Square

Parallelograms have two pairs of opposite parallel sides and two pairs of opposite congruent sides. So it is the only quadrilateral choice whose side lengths can be 10 \, cm, 6 \, cm, 10 \, cm and 6 \, cm.
6. The quadrilateral below can be classified as which of the following?

a parallelogram and a rectangle

a rectangle and a rhombus

a rectangle and a square

a parallelogram and a rhombus

A rhombus has two pairs of opposite parallel sides and two pairs of opposite congruent angles which makes it a parallelogram. It also has four congruent sides making it a special type of parallelogram.
Quadrilaterals FAQs
A quadrilateral is also a four-sided polygon or tetragon.
A trapezium is another name for a trapezoid.
You will study in detail the diagonals of quadrilaterals in middle and high school. However, they do hold special properties. The diagonals of parallelograms bisect each other.
In the special cases of parallelograms, such as rectangles, the diagonals are equal in length, in rhombuses, the diagonals are perpendicular, and in squares, the diagonals are perpendicular bisectors. Kites also have perpendicular diagonals.
A quadrangle is another name for a quadrilateral.
The next lessons are
- Perimeter
- Symmetry
- Angles in polygons
- Surface area
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!