[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!!
In order to access this I need to be confident with:
2D shapes Polygons Symmetry Line of symmetry Parallel lines Angles Types of anglesTypes of quadrilaterals
Here we will learn about types of quadrilaterals, including their names and properties and how to classify them.
Students will first learn about types of quadrilaterals as part of geometry in 4 th grade.
What are types of quadrilaterals?
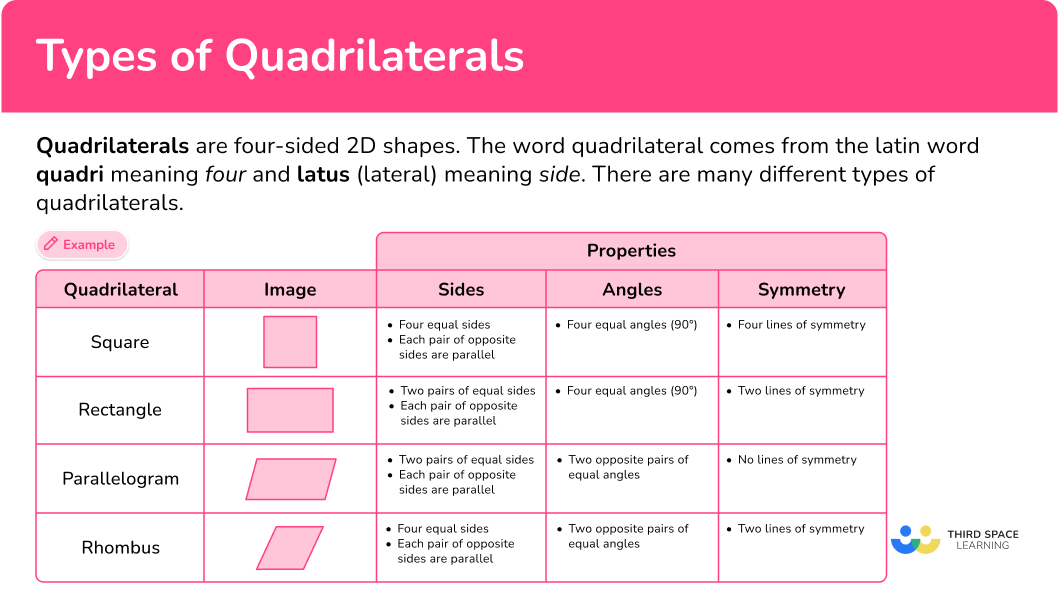
Quadrilaterals are four-sided 2D shapes. The word quadrilateral comes from the latin word quadri meaning four and latus (lateral) meaning side. There are many different types of quadrilaterals.
For example,
| Properties | ||||
|---|---|---|---|---|
| Quadrilateral | Image | Sides | Angles | Symmetry |
Square |  | ● Four equal sides
| ● Four equal | ● Four lines of |
Rectangle |  | ● Two pairs of | ● Four equal | ● Two lines of |
Parallelogram |  | ● Two pairs of | ● Two opposite | ● No lines of |
Rhombus |  | ● Four equal sides
| ● Two opposite | ● Two lines of |
Kite |  | ● Two pairs of | ● One pair of | ● One line of |
Trapezoid
|  | ● One pair of | Isosceles | ● One line of |
Irregular |  | ● No equal sides
| ● No equal | ● No lines of |
Other properties of quadrilaterals:
- The sum of the interior angles of a quadrilateral total 360^{\circ} .
- Quadrilaterals can be convex or concave.
A convex quadrilateral is a polygon with all interior angles less than 180^{\circ} . All quadrilateral shown in table above.
- A concave quadrilateral has at least one angle that is greater than 180^{\circ} (or a reflex angle).
What are types of quadrilaterals?
Common Core State Standards
How does this relate to 4 th grade math and 5 th grade math?
- Grade 4 – Geometry (4.G.2)
Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Recognize right triangles as a category, and identify right triangles.
- Grade 5 – Geometry (5.G.3)
Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category. For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles.
- Grade 5 – Geometry (5.G.4)
Classify two-dimensional figures in a hierarchy based on properties.
How to classify a quadrilateral
In order to classify a quadrilateral:
- Examine the properties of the quadrilateral, including side lengths and angle measurement.
- Name the specific type of quadrilateral.
![[FREE] End of Year Math Assessments (Grade 4 & Grade 5)](https://thirdspacelearning.com/wp-content/uploads/2023/02/end-of-year-math-assessment-grade-4-grade-5.png)
[FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREE [FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREETypes of quadrilaterals examples
Example 1: square or rectangle
Correctly classify the following quadrilateral.
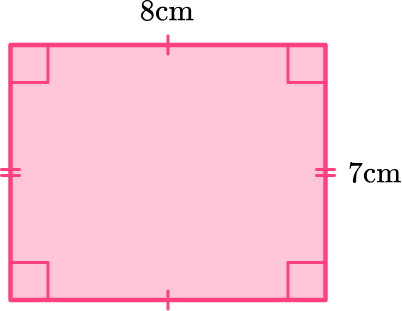
- Examine the properties of the quadrilateral, including side lengths and angle measurement.
This quadrilateral has 4 sides. The opposite sides are the same length, as shown by the tick marks. It also has 4 angles of equal measure, all of which are 90^{\circ} or right angles. This quadrilateral also has 2 pairs of parallel sides.
2Name the specific type of quadrilateral.
Since the sides are not all the same length, this quadrilateral is a rectangle, not a square. Since the shape has two pairs of parallel sides, it is also a parallelogram.
Example 2: parallelogram or rhombus
Determine what type of quadrilateral shape ABCD is.
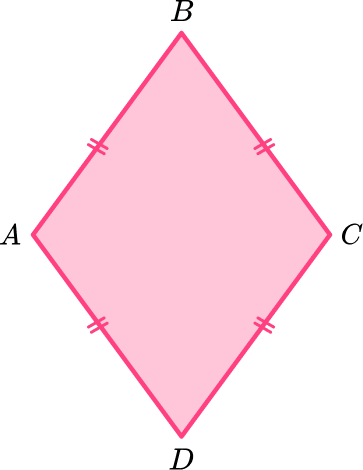
Examine the properties of the quadrilateral, including side lengths and angle measurement.
Quadrilateral ABCD has 4 equal, or congruent sides, as shown by the tick marks. It has 2 pairs of equal angles, none of which are 90^{\circ} or right angles.
Quadrilateral ABCD also has 2 pairs of parallel sides.
Name the specific type of quadrilateral.
Since it has 4 congruent sides but no right angles, quadrilateral ABCD is a rhombus, not a square.
Example 3: quadrilateral with symmetry
The polygon below is a quadrilateral. The quadrilateral has one line of symmetry along MN . By examining its properties, determine the type of quadrilateral.
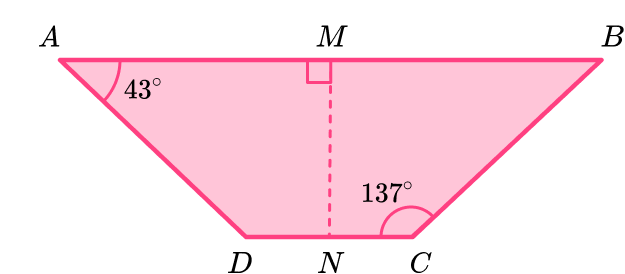
Examine the properties of the quadrilateral, including side lengths and angle measurement.
Since line MN is a line of symmetry, you know that angle A and angle B are of equal measure.
Angles D and C are also equal. This also means that side AD and side BC are congruent. This shape has one pair of parallel sides; side AB and side DC .
Name the specific type of quadrilateral.
A quadrilateral with one pair of parallel sides is a trapezoid. Since this specific trapezoid also has 2 pairs of equal angles, it is an isosceles trapezoid.
Example 4: classify quadrilaterals
Which of the following shapes can be classified as a rectangle?
Examine the properties of the quadrilateral, including side lengths and angle measurement.
Shape A : 4 equal angles (right angles), each pair of opposite sides are equal in length, 2 pairs of parallel sides.
Shape B : One pair of equal angles (right angles), one pair of parallel sides.
Shape C : 4 equal angles (right angles), 4 equal sides, 2 pairs of parallel sides.
Shape D : 4 equal angles (right angles), each pair of opposite sides are equal in length, 2 pairs of parallel sides.
Shape E : 2 pairs of equal angles, each pair of opposite sides are equal in length, 2 pairs of parallel sides.
Name the specific type of quadrilateral.
Shape A : rectangle, parallelogram
Shape B : trapezoid (specifically a right trapezoid)
Shape C : square, rectangle, parallelogram, rhombus
Shape D : rectangle, parallelogram
Shape E : parallelogram
To answer the question, Shape A and Shape D can be classified as a rectangle.
Since a square has all of the properties of a rectangle, Shape C can also be classified as a rectangle.
Example 5: name the shape
Examine the properties of the quadrilateral, including side lengths and angle measurement.
The shape has 4 sides, so it is a quadrilateral, but none of the sides are the same length. There are no angles of equal measure. The shape has no parallel sides or lines of symmetry.
Name the specific type of quadrilateral.
This shape is an irregular quadrilateral.
Example 6: word problem
Maggie drew 2 shapes. She says they are both parallelograms. Her friend Ryan said only one is a parallelogram but the other is a rhombus since it has 4 equal sides. Who is correct?
Examine the properties of the quadrilateral, including side lengths and angle measurement.
The left quadrilateral has 2 pairs of congruent sides and 2 pairs of congruent angles.
The right quadrilateral has 4 pairs of congruent sides and 2 pairs of congruent angles.
Both quadrilaterals have 2 pairs of parallel sides. Therefore, they are both parallelograms. The sides of a rhombus are all equal in length, but it still classifies as a parallelogram as well.
Name the specific type of quadrilateral.
Although Ryan said one shape is a parallelogram and one is a rhombus, which is correct, he stated that only one shape is a parallelogram. So Maggie is correct since both shapes are parallelograms.
Teaching tips for types of quadrilaterals
- Utilize visual aids such as posters, charts, or flashcards to display different types of quadrilaterals. This will help students visualize the properties of quadrilaterals and make comparisons.
- Create a worksheet with various quadrilaterals shown as shapes or objects.
- Ask students to identify and label each type of quadrilateral correctly.
- Provide additional challenge by including shapes that have characteristics of multiple types of quadrilaterals, requiring students to analyze the properties carefully.
- Provide students with practice problems that include pictures or real-life examples of objects or buildings that resemble different types of quadrilaterals. Ask them to identify and classify the objects, explaining why they think it belongs to a particular category.
Easy mistakes to make
- Incorrectly classifying quadrilaterals
Sometimes, shapes can have similarities and overlap between different types of quadrilaterals, leading to confusion. It’s important to carefully examine the properties of quadrilaterals to classify them correctly.
- Confusing a square with a rectangle
While all squares are rectangles, not all rectangles are squares. A square has equal sides, whereas a rectangle has opposite sides of equal length.
- Mistaking a rhombus for a square
A rhombus has four equal sides, but its angles are not right angles like in a square.
Related quadrilateral lessons
Practice types of quadrilaterals questions
1) Which of the following classifications does the quadrilateral NOT fit?
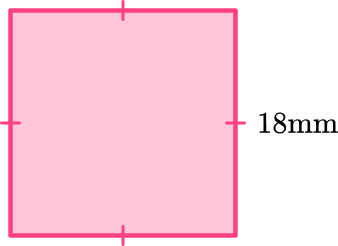
Rectangle
Square
Parallelogram
Trapezoid
This shape has 4 equal sides and 4 angles of equal measure. The 4 angles are right angles ( 90^{\circ} ). It also has 2 pairs of parallel sides. Therefore this is a square.
Based on its properties, it also classifies as a rectangle and a parallelogram. A trapezoid has only one pair of parallel sides, so this shape is not a trapezoid.
2) Determine what type of quadrilateral shape ABCD is.
Rhombus
Parallelogram
Trapezoid
Kite
This shape has 2 pairs of opposite sides that are equal and 2 pairs of angles of equal measure. It has no right angles. It has 2 pairs of parallel sides. Therefore this is a parallelogram.
3) The quadrilateral shown below has one line of symmetry on the dotted line. Name the quadrilateral.
Rectangle
Right trapezoid
Isosceles trapezoid
Parallelogram
This shape has one pair of parallel sides. Since it also has one line of symmetry and 2 pairs of equal angles, this is an isosceles trapezoid.
4) Which shape can be classified as a rhombus?
The second shape has 4 equal sides, 2 pairs of equal angles, and 2 pairs of parallel sides. Therefore it is a rhombus.
5) Use the diagram to classify the quadrilateral ABCD .
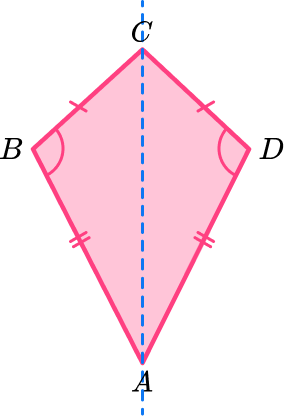
Hexagon
Kite
Rhombus
Parallelogram
Quadrilateral ABCD has two pairs of adjacent sides of equal length, and one pair of angles of equal measure. It also has one line of symmetry. It has no parallel sides. Quadrilateral ABCD is a kite.
6) The quadrilateral below can be classified as…
a parallelogram, rectangle, and square.
a parallelogram, rectangle, and rhombus.
a rectangle.
a parallelogram and rectangle.
This quadrilateral has 2 pairs of opposite sides that are equal, 4 right angles, and 2 pairs of parallel sides. That means it can be classified as a rectangle but also as a parallelogram.
Types of quadrilaterals FAQs
A quadrilateral is a polygon with four sides.
There are several types of quadrilaterals, but some common ones include squares, rectangles, parallelograms, trapezoids, and rhombuses.
A square is a quadrilateral with four equal sides and four right angles.
A rectangle is a quadrilateral with four right angles, but its opposite sides are equal in length.
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length.
A trapezoid is a quadrilateral with one pair of parallel sides. The other two sides are not parallel.
A rhombus is a quadrilateral with four equal sides. It also has opposite angles that are equal.
Yes, all squares are rectangles because they have four right angles. However, not all rectangles are squares since rectangles can have sides of different lengths.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.