[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
2D shapes Regular polygons Irregular polygons Parallel lines Perpendicular linesLines of symmetry
Here you will learn about lines of symmetry, including symmetry properties within polygons, angle properties, and symmetry of different line graphs.
Students first learn about line symmetry in grade 4 with their work with 2D shapes in geometry.
What are lines of symmetry?
Lines of symmetry are straight lines that divide a shape into two equal parts, where one part is an exact reflection or mirror image of the other.
In geometry, many 2D shapes have line symmetry.
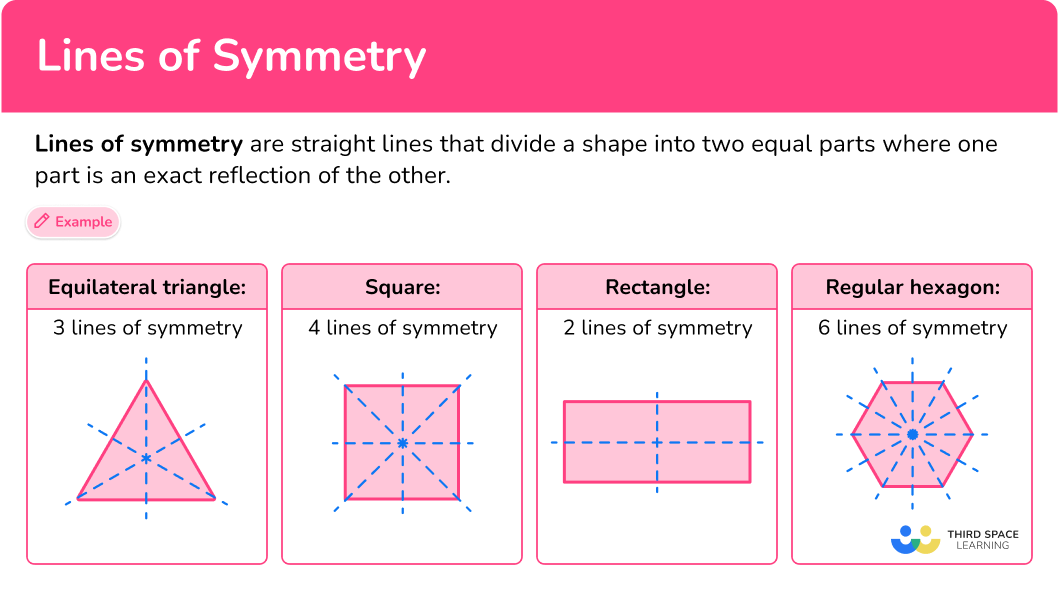
For example,
| Equilateral triangle | Square | Rectangle | Regular hexagon |
|---|---|---|---|
3 lines of symmetry  | 4 lines of symmetry  | 2 lines of symmetry  | 6 lines of symmetry  |
Line symmetry can be seen in nature.
For example,

Line symmetry can be seen in art.
For example,
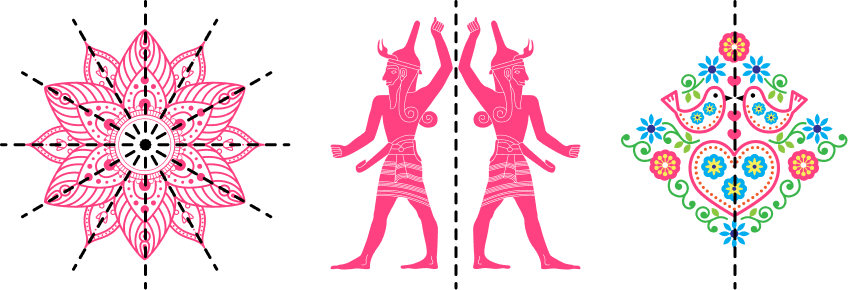
Lines of symmetry in regular shapes
Regular polygons are polygons that have equal side lengths and equal angle measures.
For example,
| Equilateral Triangle |
|---|
3 lines of symmetry 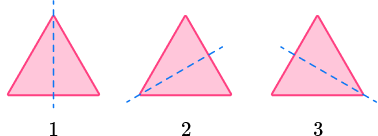 |
| Square |
4 lines of symmetry 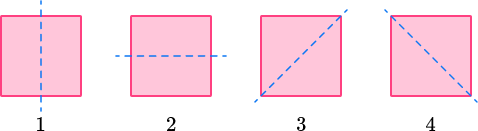 |
| Regular pentagon |
5 lines of symmetry 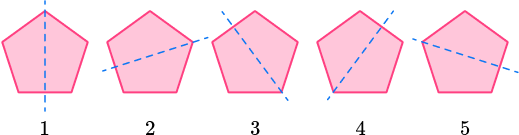 |
| Regular hexagon |
6 lines of symmetry 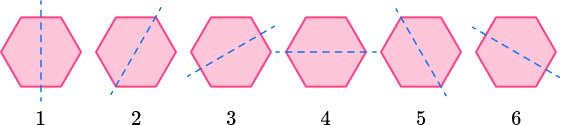 |
Notice how the number of lines of symmetry in these regular polygons is equal to the number of sides and angles the polygons have.
All regular polygons share the property that the number of sides is equal to the number of lines of symmetry.
Lines of symmetry in irregular shapes
Irregular polygons are polygons that do not have all equal angles and all equal side lengths. However, they can have line symmetry.
For example, these irregular polygons have line symmetry.
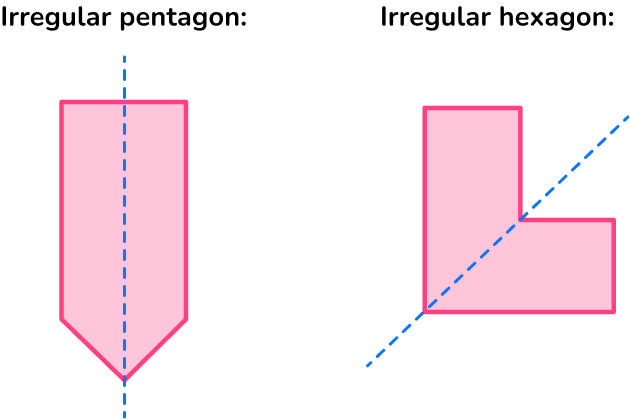
Let’s look at different shapes (specifically quadrilaterals) and their number of lines of symmetry.
| Quadrilateral | Image | Number of Lines of Symmetry |
|---|---|---|
| Square |  | 4 |
| Rectangle |  | 2 |
| Parallelogram |  | 0 |
| Rhombus |  | 2 |
| Kite |  | 1 |
| Trapezoid |  | 0 |
| Isosceles Trapezoid |  | 1 |
| Irregular |  | 0 |
Lines of symmetry in circles
The diameter of a circle splits the circle into two equal sized half circles, or semicircles. Think of the diameter as the line of reflection.
A circle can be folded in-half many ways, meaning that there are an infinite number of lines of symmetry.

What are lines of symmetry?
Common Core State Standards
How does this apply to 4th grade math?
- Grade 4: Geometry (4.G.A.3)
Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry.
How to identify lines of symmetry
In order to draw/identify lines of symmetry:
- Locate the center of the 2D shape.
- Draw a vertical line through the center and check for line symmetry.
- Draw a horizontal line through the marked center and check for line symmetry.
- Draw a line from each vertex through the center and check for symmetry.
- State the number of lines of symmetry.
![[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/07/2D-shapes-check-for-understanding-quiz-listing-image.png)
[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)
![[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/07/2D-shapes-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 2 – 4 students’ understanding of 2D shape. 10+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/07/2D-shapes-check-for-understanding-quiz-listing-image.png)
[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)
![[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/07/2D-shapes-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 2 – 4 students’ understanding of 2D shape. 10+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!
DOWNLOAD FREELines of symmetry examples
Example 1: regular shapes
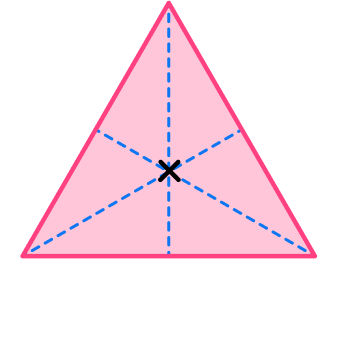
How many lines of symmetry does the equilateral triangle have?

- Locate the center of the 2D shape.

2Draw a vertical line through the center and check for line symmetry.

The vertical line through the center is a line of symmetry dividing the triangle into two equal halves that are mirror images of each other. Notice that it can be a fold line.
3Draw a horizontal line through the marked center and check for line symmetry.
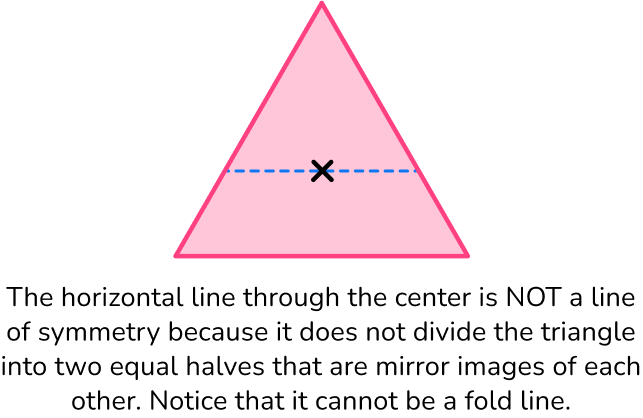
4Draw a line from each vertex through the center and check for line symmetry.
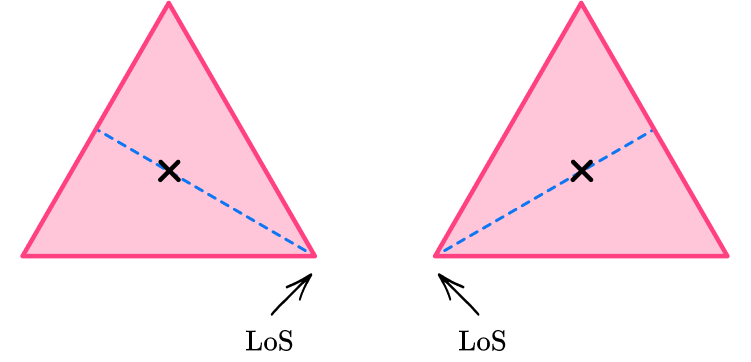
5State the number of lines of symmetry.
The equilateral triangle has 3 lines of symmetry. An equilateral triangle has 3 equal sides and 3 equal angles, so it will have 3 lines of symmetry.
Example 2: the regular pentagon
How many lines of symmetry does the regular pentagon have?

Locate the center of the 2D shape.

Draw a vertical line through the center and check for line symmetry.
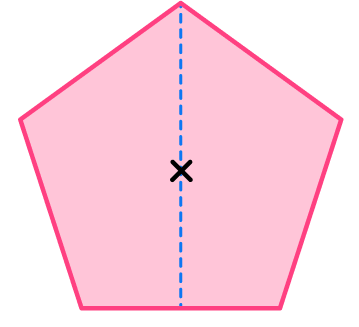
The vertical line is a line of symmetry because it divides the regular pentagon into two equal halves that are mirror images of each other.
Draw a horizontal line through the marked center and check for line symmetry.
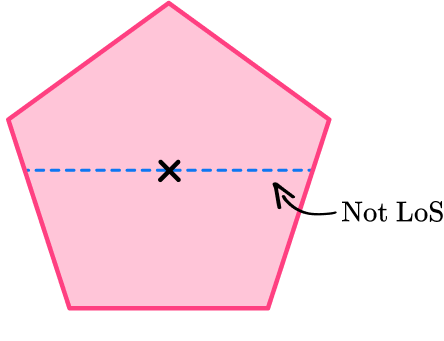
The horizontal line is NOT a line of symmetry because it does not divide the regular pentagon into two equal halves that are mirror images of each other.
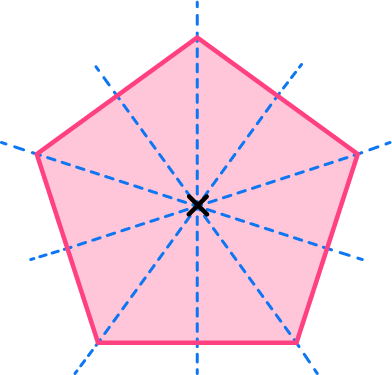
Draw a line from each vertex through the center and check for line symmetry.
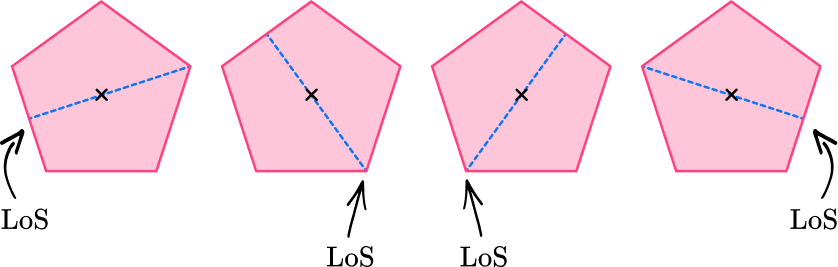
State the number of lines of symmetry.
A regular pentagon has 5 lines of symmetry. A regular pentagon has 5 equal sides and 5 equal angles, so it will have 5 lines of symmetry.
Example 3: irregular shapes
How many lines of symmetry does the trapezoid have?

Locate the center of the 2D shape.

Draw a vertical line through the center and check for line symmetry.
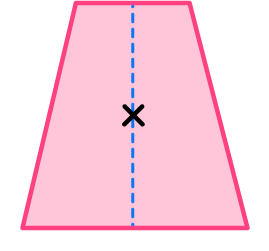
The vertical line is a line of symmetry because it divides the trapezoid into two equal halves that are mirror images of each other.
Draw a horizontal line through the marked center and check for line symmetry.
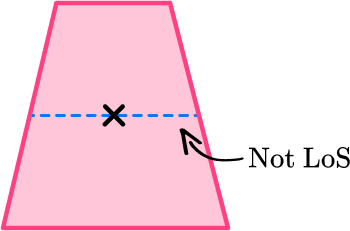
The horizontal line is NOT a line of symmetry because it does not divide the trapezoid into two equal halves that are mirror images of each other.
Draw a line from each vertex through the center and check for line symmetry.
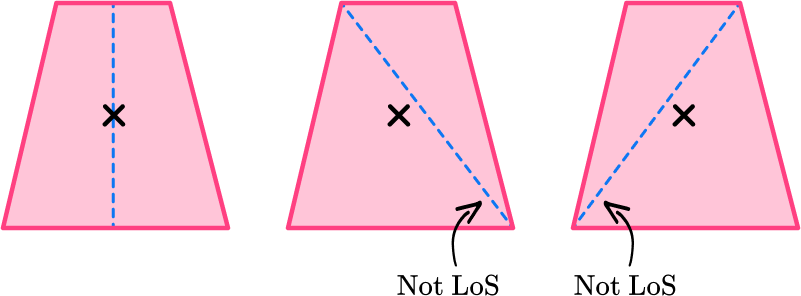
State the number of lines of symmetry.
The trapezoid has one line of symmetry.

Example 4: irregular shapes
How many lines of symmetry does the irregular hexagon have?

Locate the center of the 2D shape.

Draw a vertical line through the center and check for line symmetry.

The vertical line is a line of symmetry because it divides the irregular hexagon into two equal halves that are mirror images.
Draw a horizontal line through the marked center and check for line symmetry.

The horizontal line is a line of symmetry because it divides the irregular hexagon into two equal halves that are mirror images.
Draw a line from each vertex through the center and check for line symmetry.
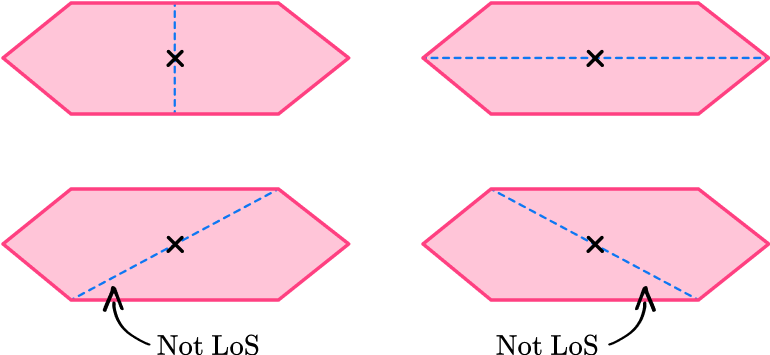
State the number of lines of symmetry.

The irregular hexagon has two lines of symmetry.
Example 5: irregular shapes
How many lines of symmetry does the parallelogram have?

Locate the center of the 2D shape.

Draw a vertical line through the center and check for line symmetry.

The vertical line is NOT a line of symmetry because it does not divide the parallelogram into two equal halves that are mirror images of each other.
Draw a horizontal line through the marked center and check for line symmetry.

The horizontal line is NOT a line of symmetry because it does not divide the parallelogram into two equal halves that are mirror images of each other.
Draw a line from each vertex through the center and check for line symmetry.
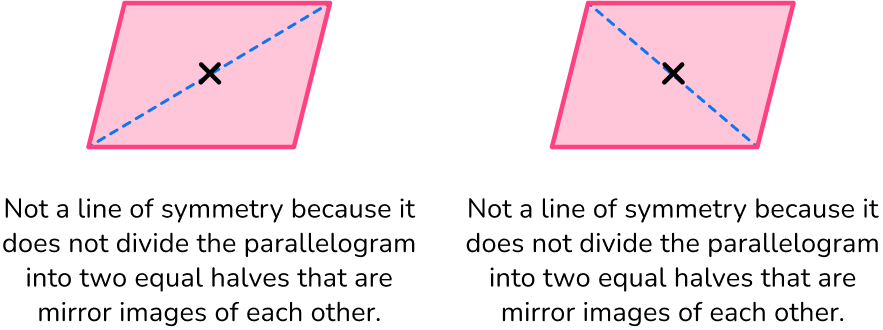
State the number of lines of symmetry.
The parallelogram does not have any lines of symmetry.
Example 6: irregular shapes
How many lines of symmetry does the shape have?

Locate the center of the 2D shape.

Draw a vertical line through the center and check for line symmetry.

The vertical line is a line of symmetry because it divides the shape into two equal halves that are mirror images of each other.
Draw a horizontal line through the marked center and check for line symmetry.
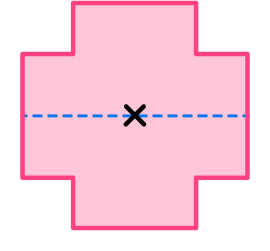
The horizontal line is a line of symmetry because it divides the shape into two equal halves that are mirror images of each other.
Draw a line from each vertex through the center and check for line symmetry.
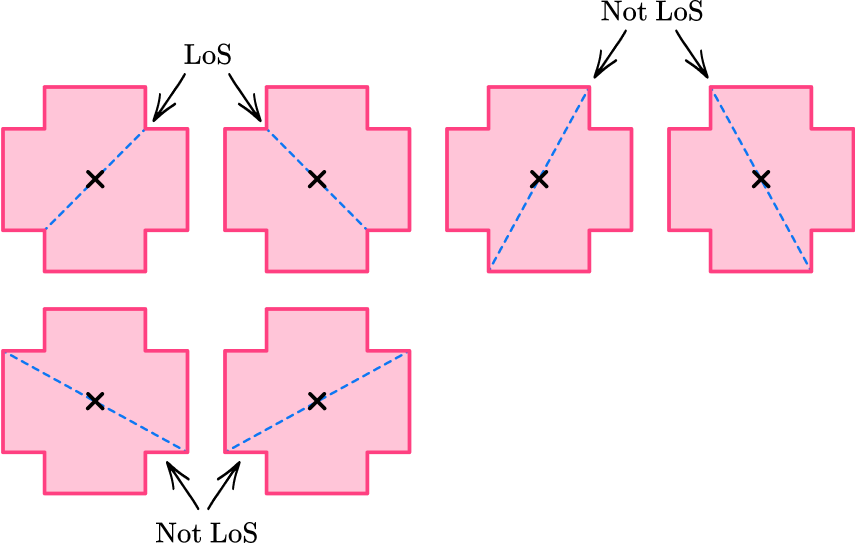
State the number of lines of symmetry.
The irregular shape has 4 lines of symmetry.
Teaching tips for lines of symmetry
- Use hands on manipulatives to help students gain understanding of lines of symmetry.
- Infuse creative activities such as origami so that students can build understanding through fun learning tasks.
Easy mistakes to make
- Not visualizing that a line of symmetry is like a fold line
For example, thinking that this is a line of symmetry. If you were to fold the parallelogram along the line of symmetry, the two halves would not be mirror images of each other.
- Thinking that all quadrilaterals have \bf{4} lines of symmetry
The only quadrilateral with 4 lines of symmetry is a square because it is a regular polygon. The other quadrilaterals are not regular polygons so do not have 4 lines of symmetry.
- The number of sides always \textbf{=} the number of lines of symmetry
Although this is true for regular shapes, it is not true for all shapes.
- Thinking all triangles have \bf{3} lines of symmetry
For example, this right scalene triangle does not have any lines of symmetry.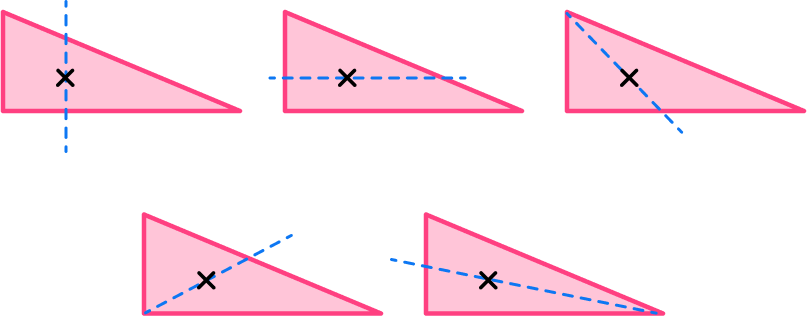
Equilateral triangles are the only triangles that have 3 lines of symmetry because it is a regular triangle.
Related symmetry lessons
- Symmetry
- Rational symmetry
Practice lines of symmetry questions
1. Find the number of lines of symmetry for the regular hexagon below.





Regular polygons have the same number of lines of symmetry as the number of sides that they have.
A hexagon has 6 sides so it has 6 lines of symmetry.
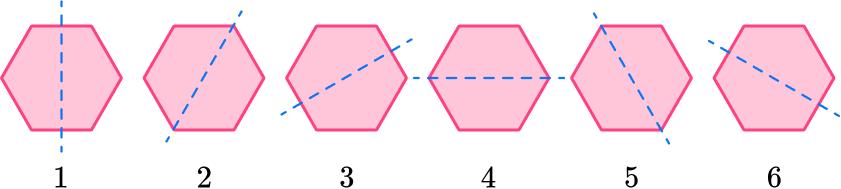
Marking the center, there are 6 lines that can be drawn through the center that cut the regular hexagon into equal halves that are mirror images of each other.
2. Find the number of lines of symmetry for the rectangle below.






After marking the center, the vertical line through the center and the horizontal line through the center are the only lines of symmetry.
Any other line drawn through the center will not result in the shape being divided into two equal halves that are mirror images.
3. Find the number of lines of symmetry for the kite below.





After marking the center, the only line of symmetry is the horizontal line.
There is no other line that can be drawn through the center that will divide the shape into two equal parts that are mirror images of each other.

4. Find the number of lines of symmetry for the irregular hexagon below.





After marking the center, the lines of symmetry are the vertical line through the center and the horizontal line through the center.
No other lines through the center will divide the shape into two equal parts that are mirror images of each other.

5. How many lines of symmetry does the smiley have?



infinite


Circles have an infinite amount of lines of symmetry. However, you have to take the eyes and mouth into account when figuring out the lines of symmetry.
There is only one line of symmetry vertically down the face that will divide the smiley face into two equal mirror images of each other.

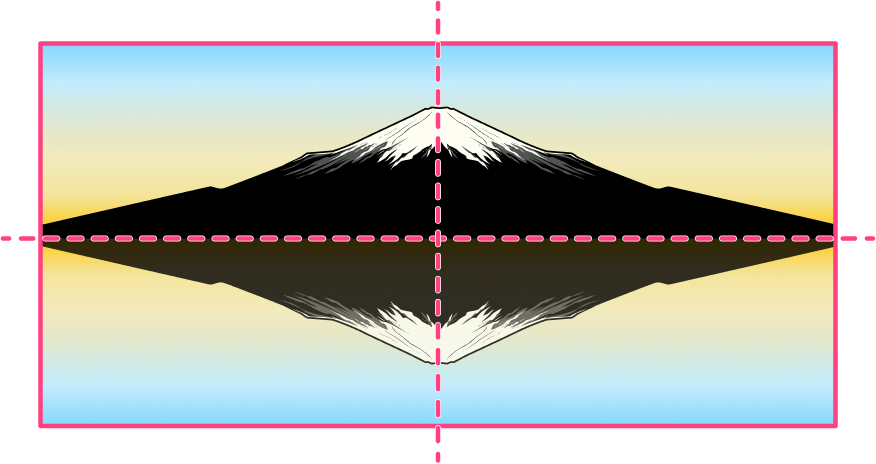
6. How many lines of symmetry does the photo have?




infinite

The photo has two lines of symmetry, one that is horizontal through the center and the other that is vertical through the center.
There are no other lines that can be drawn that divides the photo into two equal halves that are mirror images of each other.
Lines of symmetry FAQs
There are two types of symmetry. Line symmetry is drawing a line through the center of a figure where both halves are mirror images of each other. Rotational symmetry involves turning a shape and determining how many times the shape appears as its original in one complete 360^{\circ} turn.
In algebra, you will learn about quadratic functions whose graph is a parabola. The parabola has a line going through the center that divides it into identical halves, which is the axis of symmetry. It is also the line of symmetry of the parabola.
No, a scalene triangle does not have any lines of symmetry. Meaning there are no imaginary lines or mirror lines that can be drawn through the center of the triangle, where one half is equal and the mirror image of the other half. Isosceles triangles have only one line of symmetry. Equilateral triangles are regular polygons, so they have 3 lines of symmetry.
Yes, regular polygons are symmetrical shapes because they have equal sides and equal angles. They have line symmetry and rotational symmetry.
Congruent means identical in shape and size. When drawing a dotted line representing line symmetry, each half of the shape is congruent.
The next lessons are
- Angles in polygons
- Congruence and similarity
- Transformations
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!