[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
2D shapes Measuring angles Types of angles TrapezoidHypotenuse
Here you will learn about the length of the hypotenuse, using the hypotenuse to find other missing sides or angles in right angle triangles and calculating other values such as the volume or perimeter of polygons using the hypotenuse.
Students will first learn about the hypotenuse in grade 8 in geometry and will continue to work with hypotenuse concepts in high school.
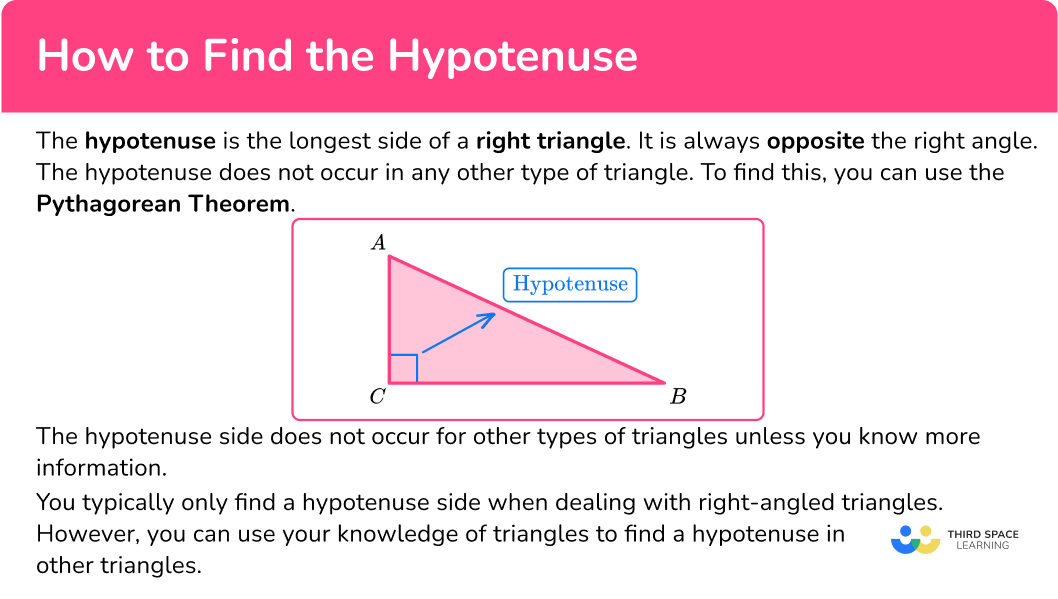
What is the hypotenuse?
The hypotenuse is the longest side of a right-angled triangle. It is the side opposite the right angle, a 90 degree angle. The word hypotenuse comes from the Ancient Greek word hypoteinousa, which means to “stretch under (a right angle)”.

The hypotenuse side does not occur for other types of triangles unless you know more information.
You typically only find a hypotenuse side when dealing with right-angled triangles. However, you can use your knowledge of triangles to find a hypotenuse in other triangles.
For example, when you know the vertical height of an isosceles triangle which is perpendicular to the base, you can create two right angle triangles within the isosceles triangle.

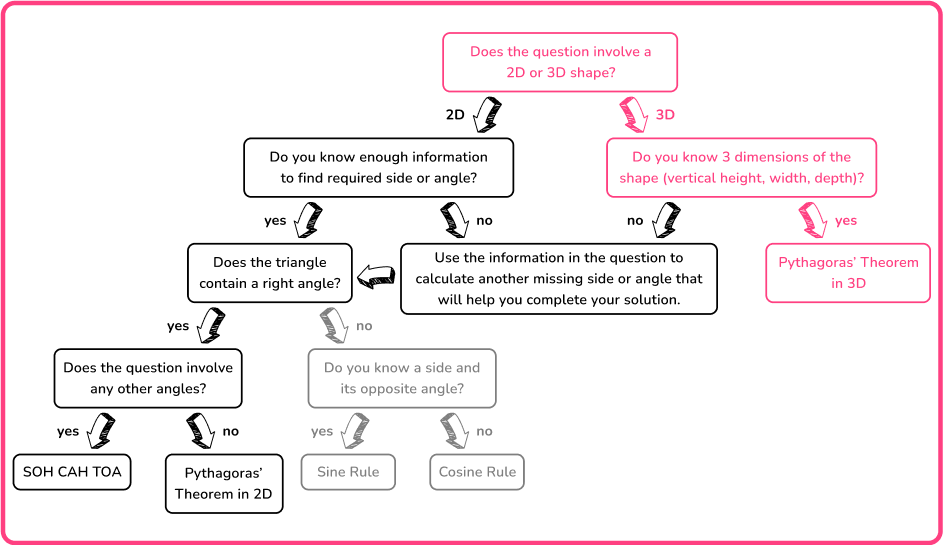
You can also calculate diagonals in 2 D and 3 D shapes by recognizing right-angle triangles. For example, you can find the diagonal length AC of a parallelogram or the diagonal length AH in the rectangular prism (cuboid) below.
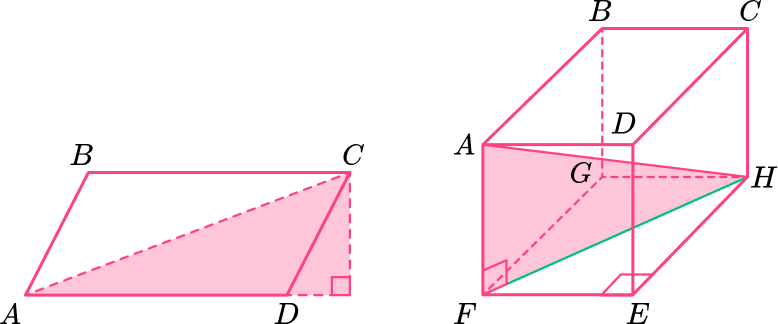
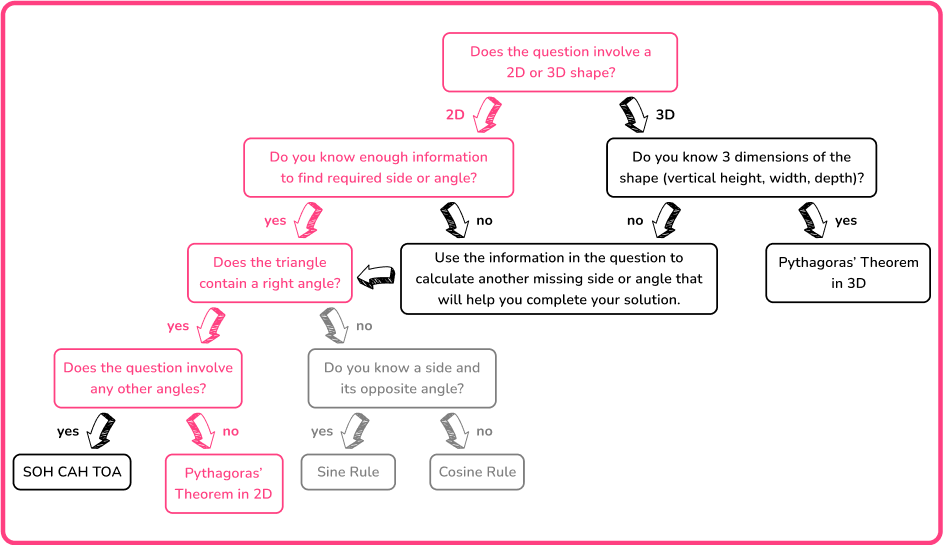
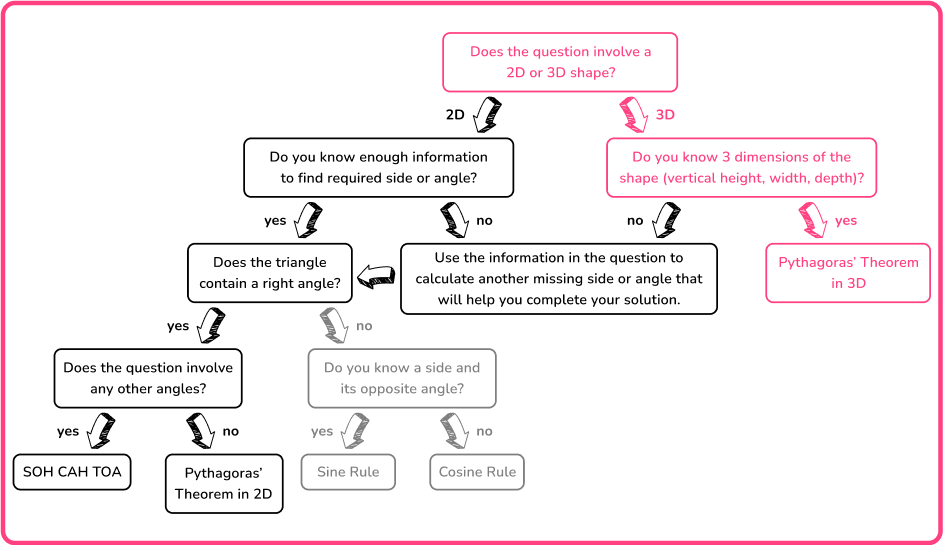
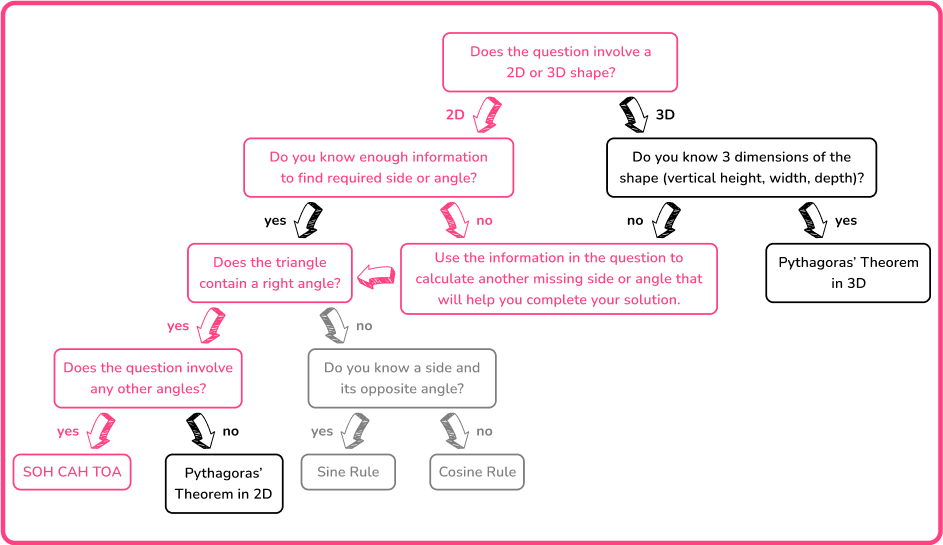
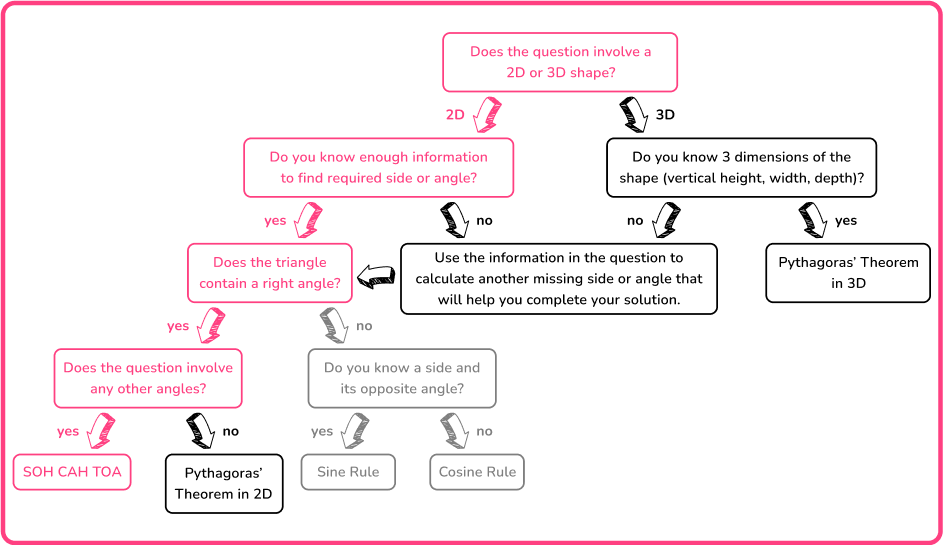
The aim of this lesson is to recognize when a problem requires you to find missing angles or sides of 2 D and 3 D shapes.
You need to be able to interpret problems and recognize whether you need to use the Pythagorean Theorem in 2 D, 3 D, or one of the three trigonometric ratios.
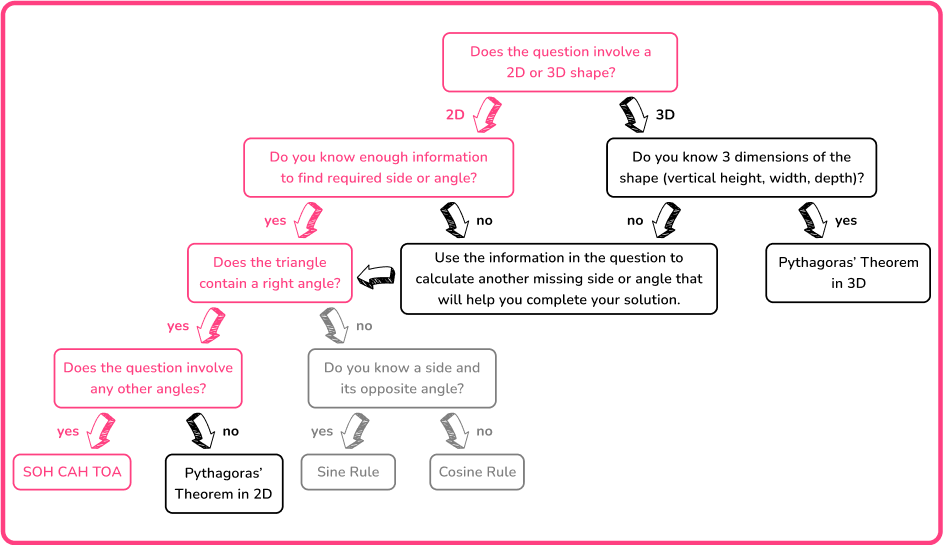
For example, you can use the following flowchart to help decide which method you need to use to solve a problem.
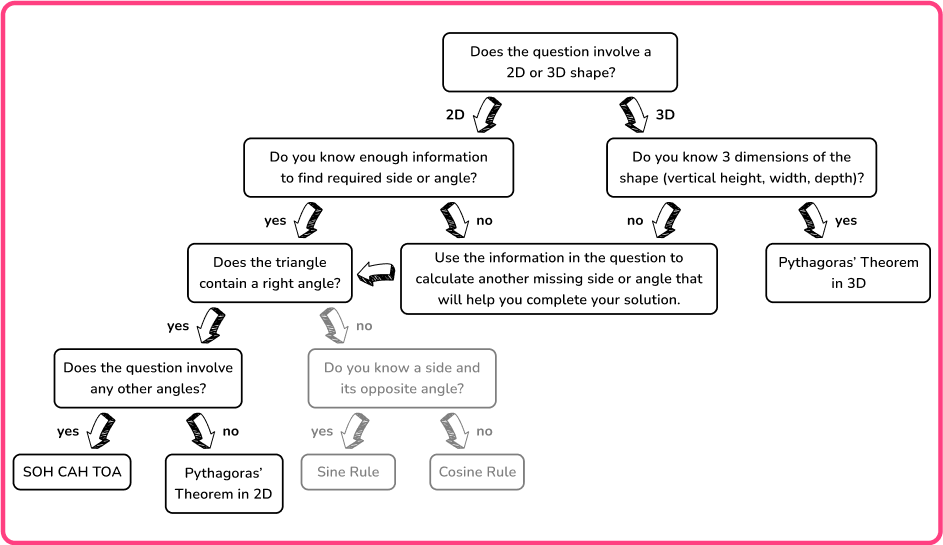
Here, the flowchart describes the information you need to know about a shape in order to solve the problem.
It is important to recognize that with most of these problems, you may need to use the Pythagorean Theorem, or trigonometry, or both within the same question so you must be confident with these topics individually to access this topic fully.
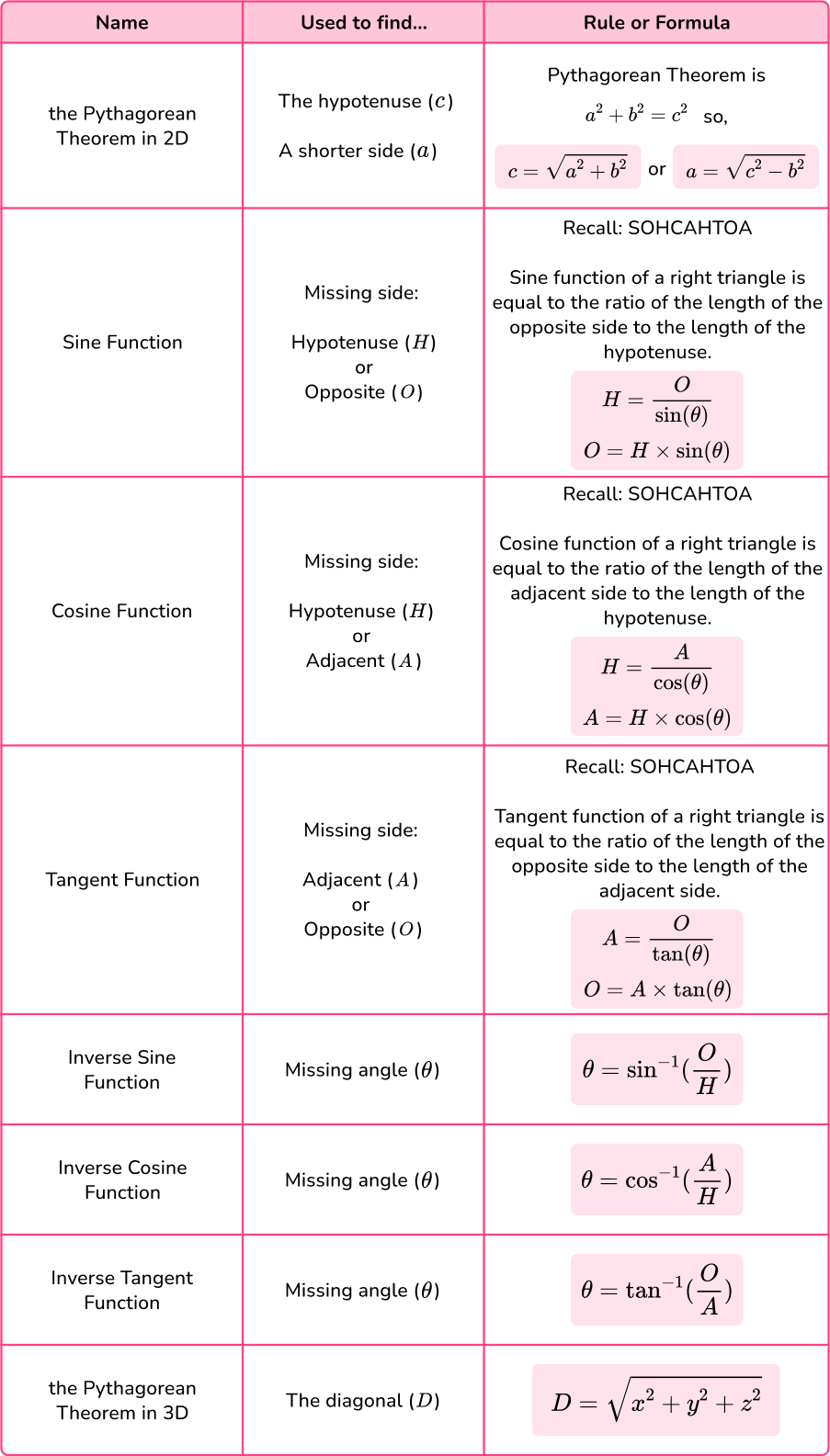
Below is a summary of the methods that can be used for right angled triangles.
What is the hypotenuse?
Common Core State Standards
How does this relate to 8 th grade and high school math?
- Grade 8 – Geometry (8.G.B.6)
Explain a proof of the Pythagorean Theorem and its converse.
- High school – Geometry – Similarity, Right Triangles and Trigonometry (HSG.SRT.B.5)
Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures.
![[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)
![[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 5 students’ understanding of triangles. 10+ questions with answers covering a range of 4th and 5th grade triangle topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)
![[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 5 students’ understanding of triangles. 10+ questions with answers covering a range of 4th and 5th grade triangle topics to identify areas of strength and support!
DOWNLOAD FREEHow to calculate the hypotenuse of any right angle triangle
In order to calculate the hypotenuse of any right angle triangle:
- Determine whether to use the Pythagorean Theorem or Trigonometry.
- Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
- Calculate the missing angle or side.
Hypotenuse examples
Example 1: find the hypotenuse using the Pythagorean Theorem
Calculate the value of x to 1 decimal place.
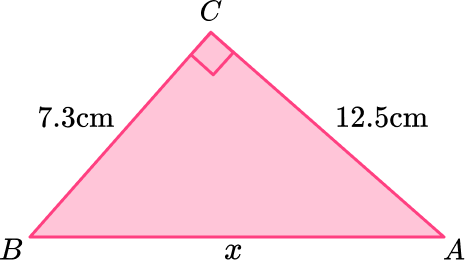
- Determine whether to use the Pythagorean Theorem or Trigonometry.
You know two missing sides of the right angle triangle and no other angles, so you can use the Pythagorean Theorem.
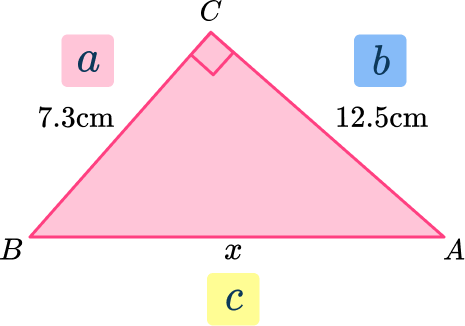
2Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Using the Pythagorean Theorem, label the sides a, \, b, and c (the opposing side to the right angle).
the Pythagorean Theorem:
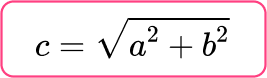
3Calculate the missing angle or side.
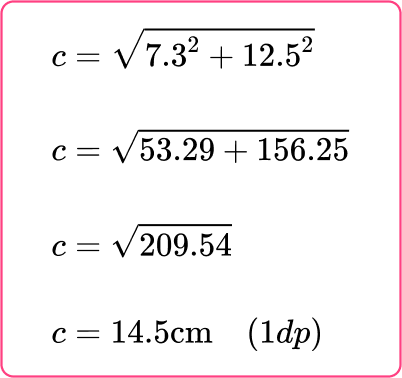
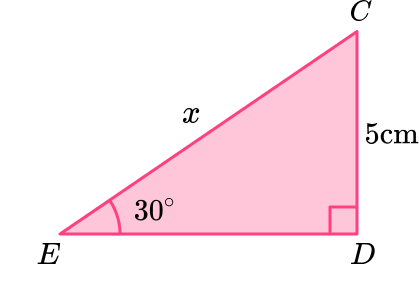
Example 2: find the hypotenuse using Trigonometry
Calculate the length of the hypotenuse of a right triangle, x, to 1 decimal place.

Determine whether to use the Pythagorean Theorem or Trigonometry.
You know one missing side of the right angle triangle and one acute angle, so you will use trigonometry to find the hypotenuse.
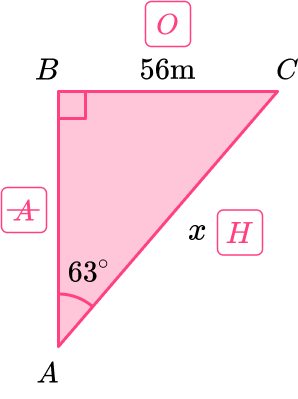
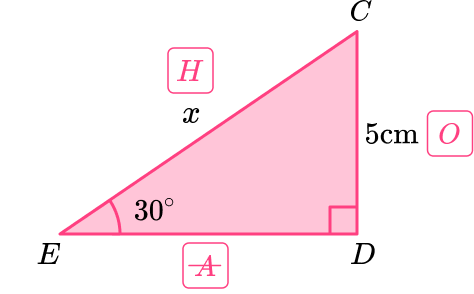
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Using trigonometry, label the sides Opposite, Adjacent and Hypotenuse according to the location of the known angle.
The two important sides in this question are the opposite side (O) and the hypotenuse (H) , so you need to use the sine function to calculate the value of x.
Sine Function:
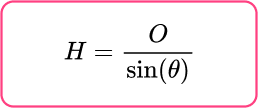
Calculate the missing angle or side.
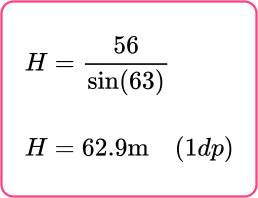
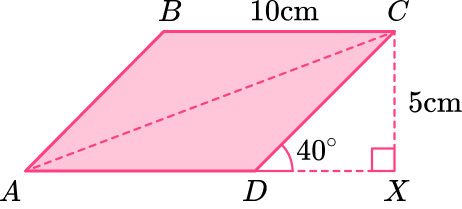
Example 3: find the diagonal of a quadrilateral
ABCD is a parallelogram. Calculate the length of the longer diagonal AC to 2 decimal places.
Determine whether to use the Pythagorean Theorem or Trigonometry.
From the information given in the diagram, you first need to calculate the base of the triangle CDX. you can then use this to find the length AC.
So you currently have to find the base of the initial triangle:
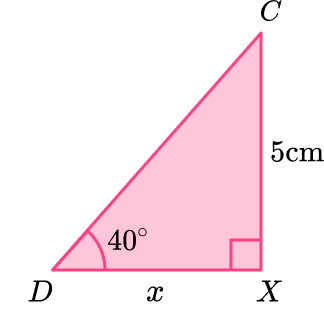
As you know one side and one angle, to calculate the base, you need to use a trigonometric ratio.
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Here you are using the tangent function as you know the opposite side to the angle and you are calculating the adjacent side.
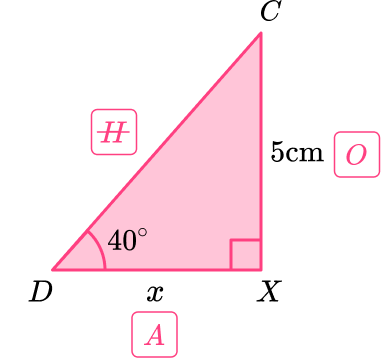
Tangent Function:
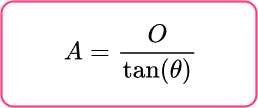
Calculate the missing angle or side.
The missing side x is therefore equal to:
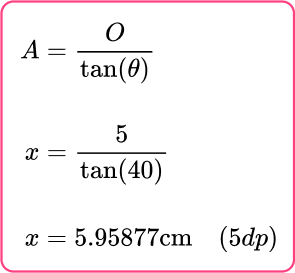
As the distance DX = 5.95877~{cm} (5~{dp}), AX = 10 + 5.95877= 15.95877~{cm} (5~{dp}).
Using this information, you can now draw the triangle ACX and calculate the length of AC.

Determine whether to use the Pythagorean Theorem or Trigonometry.
You know two sides of the right angle triangle ACX and you need to find the length of AC, you use the Pythagorean Theorem in 2 D.
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Labeling the sides of the triangle a, b, c (remember c is always the hypotenuse):
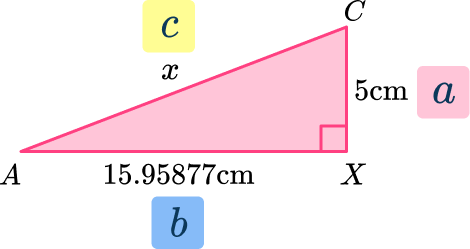
the Pythagorean Theorem:
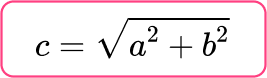
Calculate the missing angle or side.
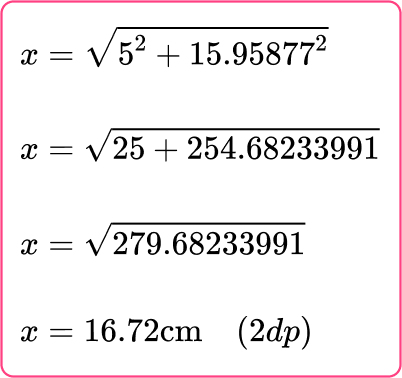
Example 4: find the diagonal of a cuboid using 3D Pythagoras
Calculate the length of the diagonal AH. Write your answer in the form a\sqrt{b}~{cm} where a and b are integers.
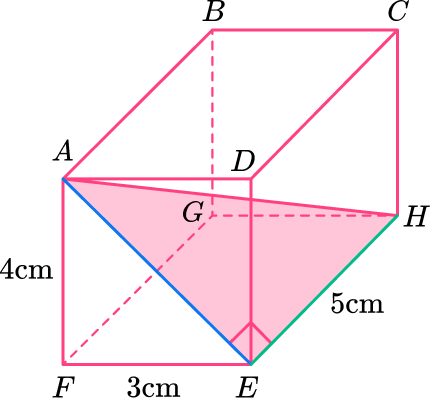
Determine whether to use the Pythagorean Theorem or Trigonometry.
You know all three dimensions of the cuboid (height, width and depth), and so you can use the Pythagorean Theorem in 3 D to calculate the length of AH.
Remember that the Pythagorean Theorem in 3 D is the sum of the squares of the lengths of the cuboid.
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Using the Pythagorean Theorem in 3 D and the side lengths of the cuboid, state the Theorem.
the Pythagorean Theorem (3 D ) :
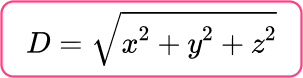
Calculate the missing angle or side.
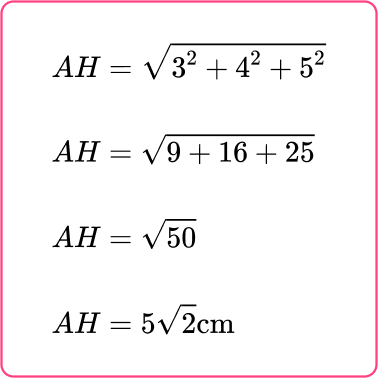
Example 5: find the missing length using trigonometry in 3D
ABCDEF is a triangular prism. Calculate the length of the line CF, correct to 3 significant figures.
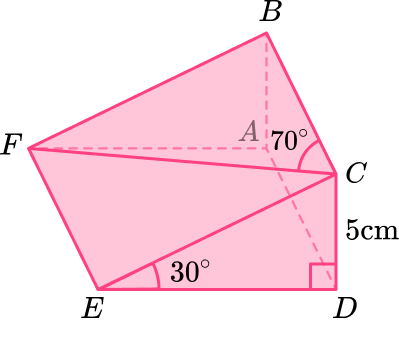
Determine whether to use the Pythagorean Theorem or Trigonometry.
From the information given in the diagram, you first need to calculate the length of CE. You can then use this to find the length CF.
So you currently have to find the hypotenuse of the initial triangle:
As you know one side and one angle, to calculate the hypotenuse, you need to use a trigonometric ratio.
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Here you are using the sine function as you know the opposite side to the angle and you are calculating the hypotenuse.
Sine Function:
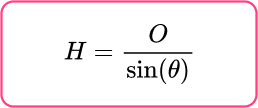
Calculate the missing angle or side.
The missing side x is therefore equal to:
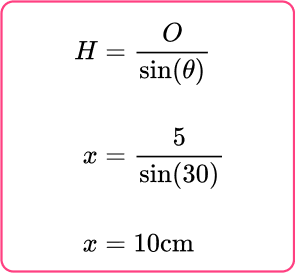
Now you know the length CE, you can use this information to draw the triangle CEF and calculate the length of CF.
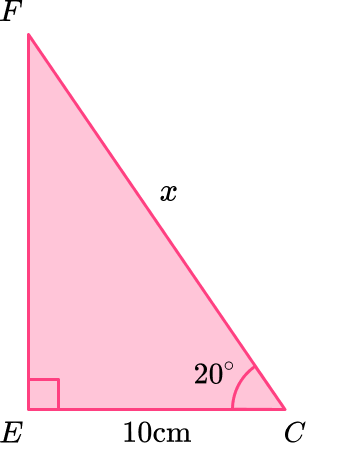
Determine whether to use the Pythagorean Theorem or Trigonometry
You know one side and one angle in the right angle triangle CEF . To find the length of CF, use trigonometry.
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Label the sides of the triangle O, A and H.
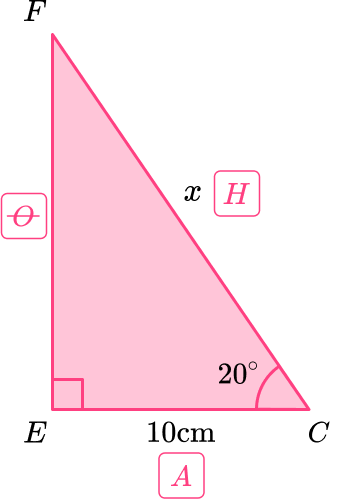
Cosine Function:
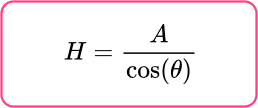
Calculate the missing angle or side.
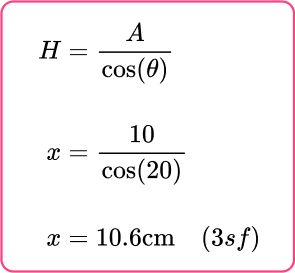
Example 6: calculating the diagonal of a 3D shape, given the volume
The cube shown has a volume of 648\sqrt{3} \, \mathrm{cm}^{3}. Calculate the length of the diagonal AH.
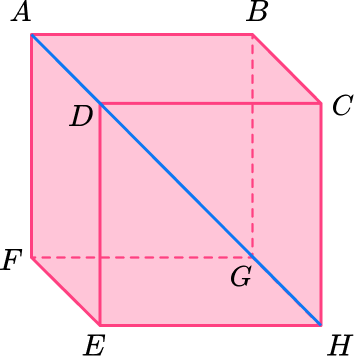
Determine whether to use the Pythagorean Theorem or Trigonometry.
To find the diagonal, you need to know the side length of the cube. Calculate this first using the volume. The volume of a cube is the cube of the side length, so you need to cube root the volume of 648\sqrt{3} \, \mathrm{cm}^{3} to calculate the side length.
Here you will find EH:
EH=\sqrt[3]{648\sqrt{3}}\
EH=6\sqrt{3} \, \mathrm{cm}\
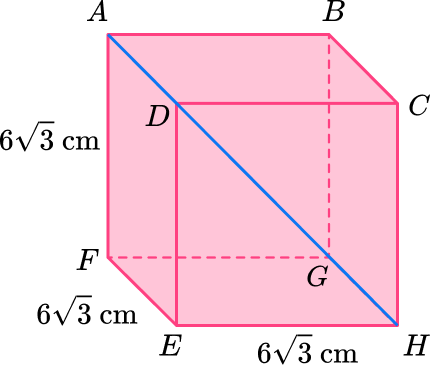
Each side length of the cube is equal to 6\sqrt{3} \, \mathrm{cm} , so you can use the Pythagorean Theorem in 3 D as you know the height, width and depth of the shape.
Label the right angle triangle \textbf{(abc} or \textbf{OAH}) and state the formula/rule used.
Here, as you are using the Pythagorean Theorem in 3 D and you know the side lengths of the cube, you can just state the Theorem.
the Pythagorean Theorem (3 D):
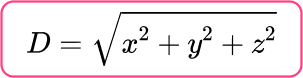
Calculate the missing angle or side.
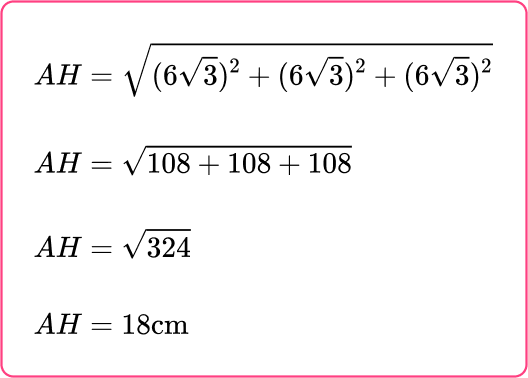
Teaching tips for hypotenuse
- Start with a review of triangles, including definitions of the various sides and angles. Emphasize that every triangle has one side that is the longest side – this is called the hypotenuse. Prompt students to think about the word hypotenuse and come up with their own definition after knowing where it is located.
- Use visual examples and have students identify the hypotenuse in different types of triangles drawn on the board. Right triangles, isosceles triangles, and scalene triangles should all be shown.
Allow students to draw their own similar triangles and work with partners to allow them to solidify their understanding in a concrete way. This is a great scaffolding opportunity for English language learners and allows them to engage with other students to strengthen their foundational knowledge.
- Give students hypotenuse practice problems of increasing difficulty. Start with triangles where all sides but the hypotenuse are given. Then provide triangles missing one of the short sides as well.
- Use real world examples like images of construction sites, roofing, ladders against walls, etc. Have students identify the hypotenuse in each practical application.
Easy mistakes to make
- Forgetting that the hypotenuse is the longest side
The hypotenuse is always opposite the right angle and is the longest side of a right triangle. Students may incorrectly identify one of the legs as the hypotenuse if they forget this key aspect.
- Mixing up leg and hypotenuse labels in the Pythagorean theorem
When finding a missing hypotenuse using c^{2}=a^{2}+b^{2} the hypotenuse is always labeled c. Mixing up what sides correspond to a, b and c can lead to an incorrect answer.
- Finding an area or perimeter instead of the hypotenuse
The Pythagorean theorem finds the missing side length, not an area or perimeter. Students trying to apply the a \times b = c formula for area can make this misunderstanding.
- Using the wrong operation when multiple operations are required
Finding a missing hypotenuse requires squaring, adding, and square roots. Switching the order of operations or using the wrong ones (for example, multiplying instead of squaring) is an easy mistake for 8 th graders learning these procedural skills.
Related triangles lessons
- Types of triangles
- Right triangle
- Acute triangles (coming soon)
- Equilateral triangle
- Isosceles triangle
- Scalene triangle
Practice hypotenuse questions
1) Triangle ABC is a right angle triangle. Calculate the value of x.
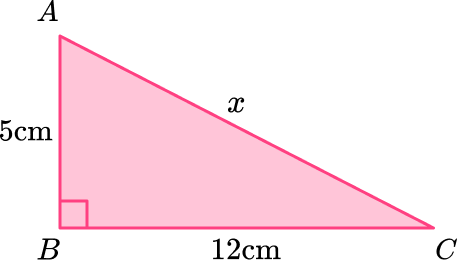




This is a right angled triangle and you do not know any of the angles, so you need to use the Pythagorean Theorem.
\begin{aligned} c^{2}&=a^{2}+b^{2}\\\\ x^{2}&=5^{2}+12^{2}\\\\ x^{2}&=25+144\\\\ x^{2}&=169\\\\ x&=13 \, \mathrm{cm} \end{aligned}
2) Calculate the value of \theta to 2 significant figures.
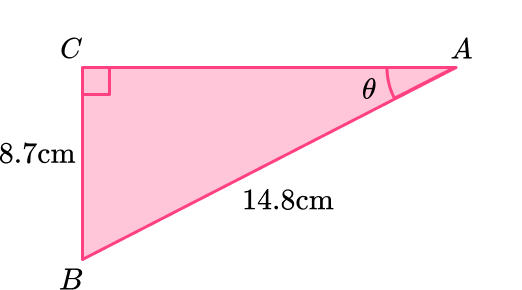




This is a right angled triangle and you are working out the size of an angle, so you need to use SOHCAHTOA.
\begin{aligned} \sin(\theta)&=\cfrac{O}{H}\\\\ \sin(\theta)&=\cfrac{8.7}{14.8}\\\\ \theta&= \sin^{-1}(\cfrac{8.7}{14.8})\\\\ \theta&=36^{\circ} \end{aligned}
3) ABCD is a trapezoid with diagonal length 10~{cm}. Calculate \theta, the external angle of the polygon at B, round to 2 decimal places.
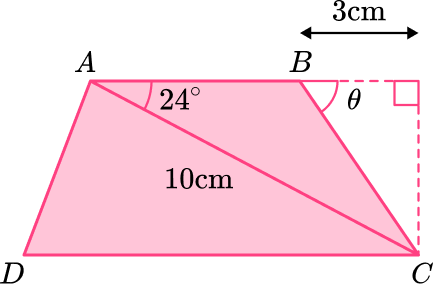




First you need to calculate the height of the trapezoid. You can do this using the following triangle:
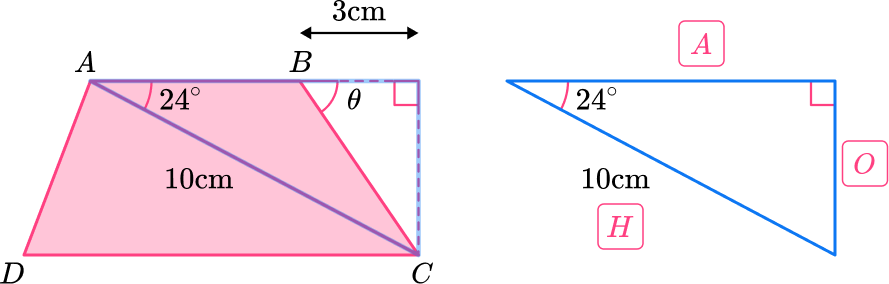
The triangle is a right angle triangle, and you know an angle, so you need to use SOHCAHTOA. You want to work out O , and you know H , so use sin.
\begin{aligned} O&=H \sin(\theta)\\\\ O&=10 \sin(24)\\\\ O&=4.067366431 \end{aligned}
Use the height, along with the information you have been given to find the angle. You know O and A , so use tan.
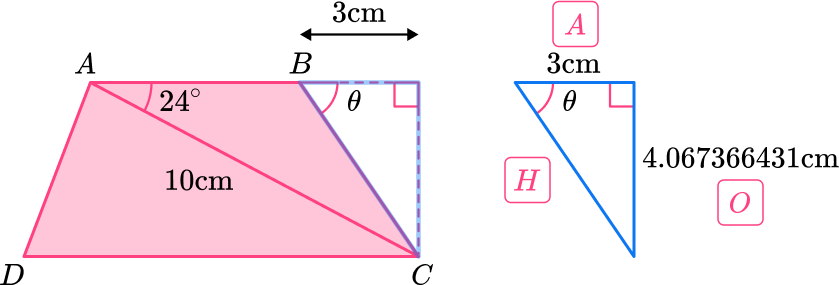
\begin{aligned} \tan(\theta) &= \cfrac{O}{A}\\\\ \tan(\theta)&=\cfrac{4.067366431}{3}\\\\ \theta&=\tan^{-1}(\cfrac{4.067366431}{3})\\\\ \theta&=53.59^{\circ} \end{aligned}
4) A swimming pool is the shape of a trapezoidal prism. A sketch of the swimming pool is drawn below.
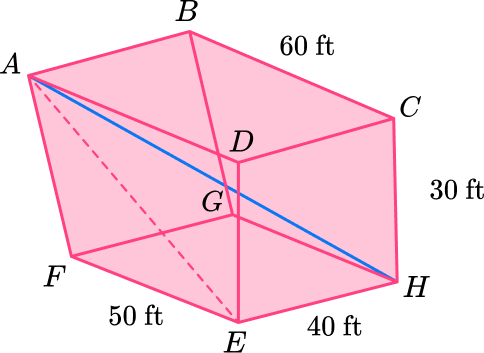
Calculate the longest distance in the pool, AH, correct to 3 significant figures.




Here you need to calculate the diagonal length of a 3 D shape for which you know the length, width and depth. You can apply the Pythagorean Theorem in 3 D.
\begin{aligned} D^{2}&=x^{2}+y^{2}+z^{2}\\\\ D^{2}&=30^{2}+40^{2}+60^{2}\\\\ D^{2}&=6100\\\\ D&=78.1 \, \mathrm{ft} \end{aligned}
5) ABC and ADE are two right angle triangles where AD=\cfrac{2}{3}AC,
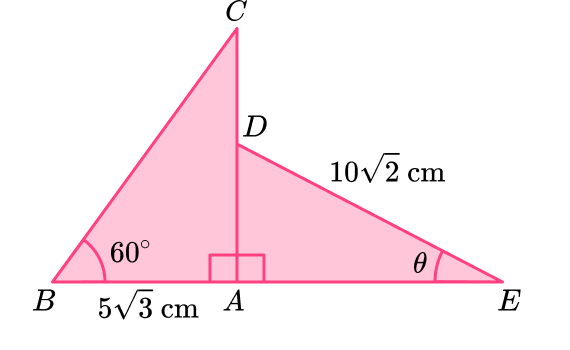
By calculating the length of AD, find the value of \theta.




First, you need to calculate the length AC.
ABC is a right angled triangle, and you know an angle, so you can use SOHCAHTOA.
You know A and you want to work out O , so use tan.
\begin{aligned} O&=A\tan(\theta)\\\\ O&=5\sqrt{3}\tan(60)\\\\ O&=15 \, \mathrm{cm} \end{aligned}
You are given,
AD=\cfrac{2}{3}AC
Therefore,
AD=\cfrac{2}{3} \times 15=10 \, \mathrm{cm}
Now that you know the length AD, you can use the triangle ADE to calculate the required angle.
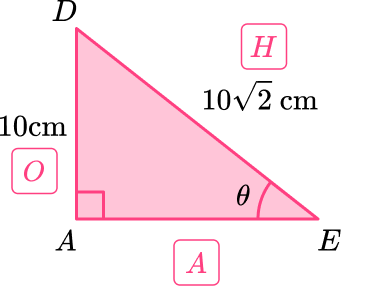
You know O and H so use sin.
\begin{aligned} \sin(\theta)&=\cfrac{O}{H}\\\\ \sin(\theta)&=\cfrac{10}{10\sqrt{2}}\\\\ \theta&=\sin^{-1}(\cfrac{10}{10\sqrt{2}})\\\\ \theta&=45^{\circ} \end{aligned}
6) The surface area of a cube below is equal to 150~{cm}^2. Find the diagonal length BE. Give your answer in square root form.
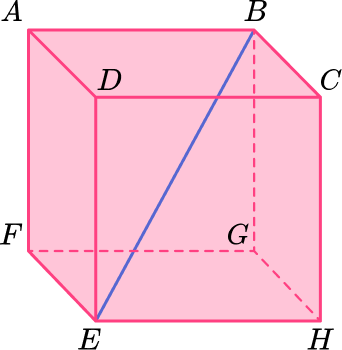




This is a cube so all 6 faces are the same.
If the surface area is 150~{cm}^2, then the area of each face is 150\div 6=25 \, \mathrm{cm}^{2} and the length of each side is \sqrt{25}=5 \, \mathrm{cm}.
You can then use the Pythagorean Theorem in 3 D to find the length of the diagonal:
\begin{aligned} D^{2}&=x^{2}+y^{2}+z^{2}\\\\ D^{2}&=5^{2}+5^{2}+5^{2}\\\\ D^{2}&=75\\\\ D&=5\sqrt{3} \, \mathrm{cm} \end{aligned}
Hypotenuse FAQs
This has to do with the order of operations within the Pythagorean theorem formula. You first have to square the leg lengths because that formula requires finding the sum of the squares.
After adding them, you take the square root because the final number represents the actual hypotenuse length, not its square. Think of solving one step at a time – first sum the squares, then resolve to the side length.
No, the definition of a hypotenuse is that it is the longest side of a right triangle, directly opposite the right angle. If the side opposite the right angle is the shortest, then it cannot be labeled as the hypotenuse.
Those side length relationships do not align with the properties and labeling conventions of right triangles.
No, not always. If you already know the length of all 3 sides of a right triangle, you can just identify the longest side as the hypotenuse without using any formulas. But if you only know 2 side lengths and need to find the third, Pythagorean theorem is the go-to method.
Being able to find missing side lengths, especially the longest one, is important for a variety of mathematical and real-world applications. From finding distances to constructing structures at specific dimensions, knowing hypotenuse lengths has many practical uses.
The concepts are also foundational for higher level math and physics formulas.
An isosceles right triangle has one right angle, 90 degrees, and two congruent angles, 45 degrees each. Because the triangle has two equal sides, you can simplify the Pythagorean Theorem to c^{2}=a^{2}+a^{2}. You can then solve the equation.
The Law of Sines is a trigonometric equation that relates the lengths of the sides of a triangle to the sines of its angles.
It can be expressed as, \cfrac{a}{\sin A}=\cfrac{b}{\sin B}=\cfrac{c}{\sin C} \, .
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!