[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Place value Addition and subtraction Types of anglesMeasuring angles
Here you will learn about measuring angles, including how to measure an angle using a protractor.
Students first learn about measuring angles as part of geometry in 4 th grade. They expand that knowledge as they progress through middle school and high school.
What is measuring angles?
Measuring angles is finding the number of degrees an angle is. Angles are measured in degrees using the degree sign ^{\circ} . The tool used for measuring angles is called a protractor.
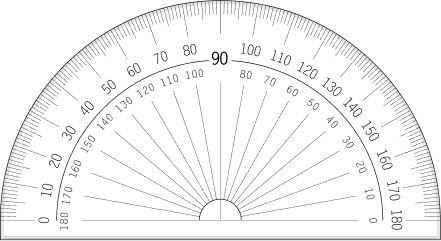
The degree measure on the top center of a protractor is 90^{\circ} . This is the midpoint of the protractor. Note that the numbers to the left and to the right of the center either go up by ten or go down by ten degrees.
If the angle is acute, you will use the acute measurement (less than 90^{\circ} but greater than 0^{\circ} ), and if the angle is obtuse, you will use the obtuse measurement (greater than 90^{\circ} but less than 180^{\circ} ).
For example, let’s look at the measure of ∠D.
The vertex of the angle, D , is placed on the bottom center of the protractor. One arm of the angle is lined up with the bottom of the protractor at 0^{\circ} . The other arm is used to measure the turn from one arm to the next.
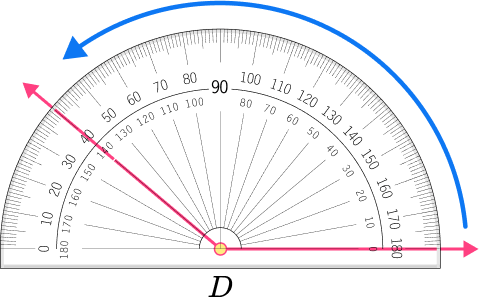
Notice how the arm goes through the measure of 40^{\circ} and 140^{\circ} . Since the angle is obtuse, use the measurement that is greater than 90^{\circ} and less than 180^{\circ} . The angle measure 140^{\circ} .
The angle on a protractor may not always line up with the bottom of the protractor at zero. If this happens, you will subtract in order to find the measurement of the angle.
For example, let’s look at the measure of ∠abc.
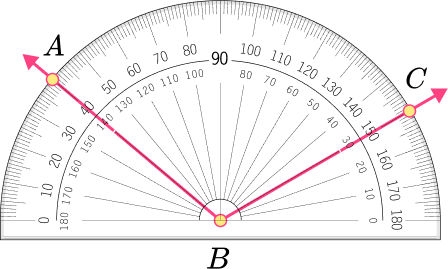
Notice how both point A and C are on an angle measure greater than zero. You will have to subtract in order to find the measure of the angle. In order to calculate the correct measure, decide whether to use the top angle measurements or bottom angle measurements.
If using the top angle measurements, notice the arms of the angles read 150^{\circ} and 40^{\circ} . If using the bottom angle measurements, notice the arms of the angles read 140^{\circ} and 30^{\circ} .
To find the measure of the angle, you will subtract the two angle measurements.
150-40=110^{\circ}
140-30=110^{\circ}
The measure of the angle is 110^{\circ} .
What is measuring angles?
Common Core State Standards
How does this apply to 4 th grade math and 7 th grade math?
- Grade 4 – Measurement and Data (4.MD.C.6)
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
- Grade 4 – Measurement and Data (4.MD.C.7)
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, example, by using an equation with a symbol for the unknown angle measure.
- Grade 7 – Geometry (7.G.B.5)
Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
![[FREE] Angles Check for Understanding Quiz (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Check for Understanding Quiz (Grade 4)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] Angles Check for Understanding Quiz (Grade 4)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREEHow to measure angles
In order to measure an angle, you need to:
- Determine the type of angle.
- Check to make sure the vertex is at the center of the protractor and one side of the angle is lined up with the bottom of the protractor.
- Find the degree measure.
Measuring angle examples
Example 1: arm of angle is lined up with zero
Find the measure of the given angle.
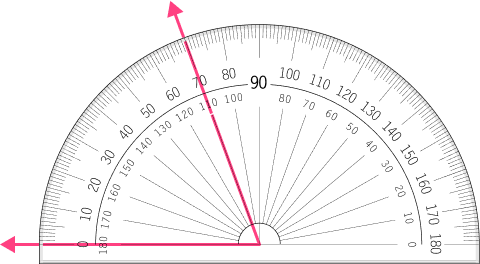
- Determine the type of angle.
The angle is an acute angle because it appears to be less than 90^{\circ} .
2Check to make sure the vertex is at the center of the protractor and one side of the angle is lined up with the bottom of the protractor.
The vertex is placed correctly on the protractor. The arm is lined up correctly on the bottom of the protractor.
3Find the degree measure.
The other arm goes through the 70^{\circ} and 110^{\circ} . Since the angle is acute, the correct measure is 70^{\circ} .
Example 2: arm of angle is lined up with zero
Find the measure of the given angle.
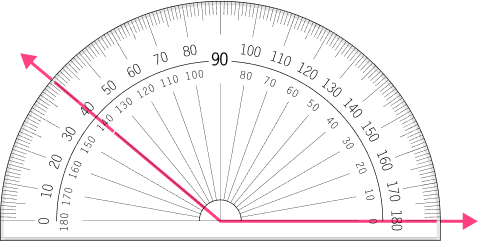
Determine the type of angle.
The angle is an obtuse angle because it appears to be greater than 90^{\circ} .
Check to make sure the vertex is at the center of the protractor and one side of the angle is lined up with the bottom of the protractor.
The vertex is placed correctly on the protractor. The arm is lined up correctly on the bottom of the protractor.
Find the degree measure.
The other arm goes through the 40^{\circ} and 140^{\circ} . Since the angle is obtuse, the correct measure is 140^{\circ} .
Example 3: arm of angle is lined up with zero
Find the measure of the given angle.
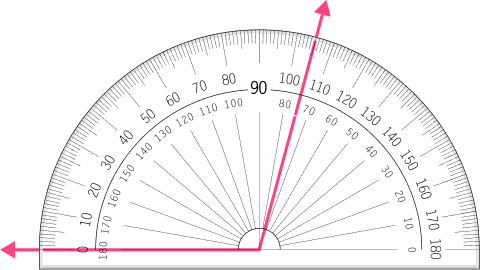
Determine the type of angle.
The angle is an obtuse angle because it appears to be greater than 90^{\circ} .
Check to make sure the vertex is at the center of the protractor and one side of the angle is lined up with the bottom of the protractor.
The vertex is placed correctly on the protractor. The arm is lined up correctly on the bottom of the protractor.
Find the degree measure.
The other arm goes through the 75^{\circ} and 105^{\circ} . Since the angle is obtuse, the correct measure is 105^{\circ} .
How to measure angles that are not aligned at zero
In order to measure an angle that is not aligned at zero, you need to:
- Determine the type of angle.
- After deciding which degree measures to use, find the degree measure for each arm.
- Subtract the degree measures.
- State the number of degrees measured.
Example 4: arm of angle is not lined up with zero
Find the measure of the given angle.
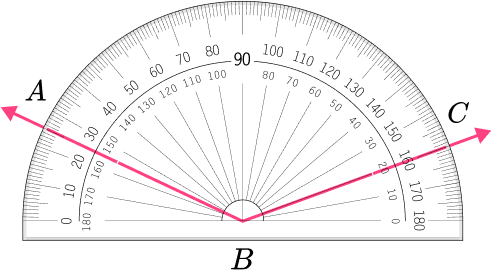
Determine the type of angle.
Angle ABC is an obtuse angle because it appears to be greater than 90^{\circ} .
After deciding which degree measures to use, find the degree measure for each arm.
Using the measures that run from left to right, the arm at point A goes through 25^{\circ} , and the arm at point C goes through 160^{\circ} .
Subtract the degree measures.
Subtract the two measures,
160-25=135
State the number of degrees measured.
The measure of angle ABC is 135^{\circ} .
Example 5: arm of angle is not lined up with zero
Find the measure of the given angle.
Determine the type of angle.
The angle is an acute angle because it appears to be less than 90^{\circ} .
After deciding which degree measures to use, find the degree measure for each arm.
Using the measures that run from left to right, the arm at point A goes through 45^{\circ} , and the arm at point C goes through 90^{\circ} .
Subtract the degree measures.
Subtract the two measures,
90-45=45
State the number of degrees measured
The measure of angle ABC is 45^{\circ} .
Example 6: arm of angle is not lined up with zero
Find the measure of the given angle.
Determine the type of angle.
The angle is an acute angle because it appears to be less than 90^{\circ} .
After deciding which degree measures to use, find the degree measure for each arm.
Using the measures that run from left to right, the arm at point A goes through 33^{\circ} , and the arm at point C goes through 119^{\circ} .
Subtract the degree measures.
Subtract the two measures,
119-33=86
State the number of degrees measured.
The measure of angle ABC is 86^{\circ} .
Teaching tips for measuring angles
- Introduce the protractor by allowing students to use and investigate the tool. Make sure students are comfortable with the different parts of the protractor including the straight edge, the curved edge with degree markings and the midpoint.
- Before jumping into measuring, make sure students are able to identify the different types of angles: acute angle, obtuse angle, right angle, straight angle, and reflex angle.
- While angle worksheets have their place when working with measuring angles, allowing students to have real-world practice using protractors in the classroom is important. Allow students to draw angles and practice measuring the angle using a protractor.
Easy mistakes to make
- The midpoint of the protractor is not properly aligned with the vertex
When finding the measure of an angle, it is important to make sure that the vertex of the angle is lined up correctly with the midpoint of the protractors.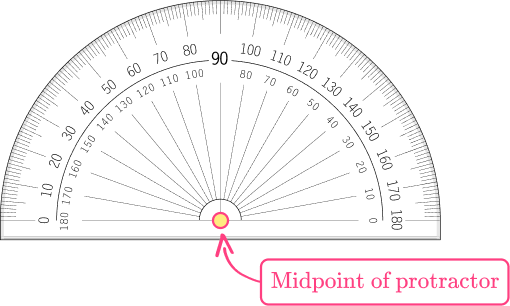
- Reading the wrong scale when measuring angles
A protractor has two different sets of degree markings at the top, one that reads from left to right, and one that reads from right to left. Make sure you have identified the type of angle (acute or obtuse) before deciding which angle markings to read from.
- Confusing the different types of angles
Before beginning to measure angles, it’s important that the student is familiar with the different types of angles.
Related angles lessons
- Angles
- Types of angles
- Acute angle
- Obtuse angle
- Right angle
- Adjacent angles
- Complementary angles
- Supplementary angles
- Geometry theorems
- Vertical angle theorem
- Straight angle
- Angles point
- Pentagon angles
Practice measuring angles questions
1. What is the measure of angle LMN to the nearest degree?
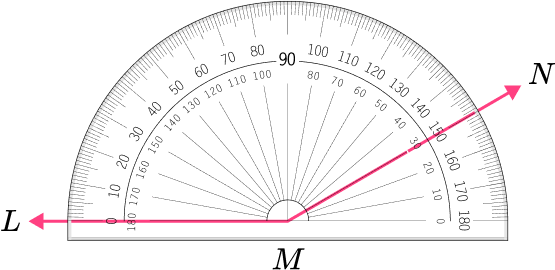
The vertex is placed correctly on the protractor and the arm is lined up correctly on the bottom of the protractor.
The angle is an obtuse angle because it appears to be greater than 90^{\circ} .
The other arm goes through the 150^{\circ} and 30^{\circ} . Since the angle is obtuse, the correct measure is 150^{\circ} .
2. Which angle has a measure closest to 85^{\circ} ?
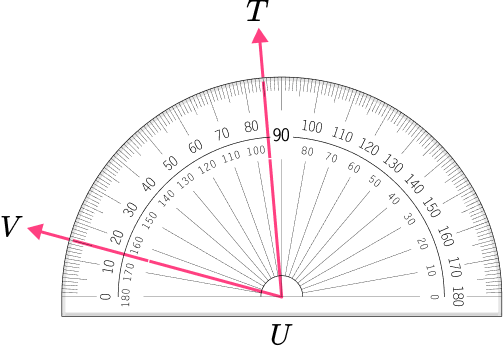
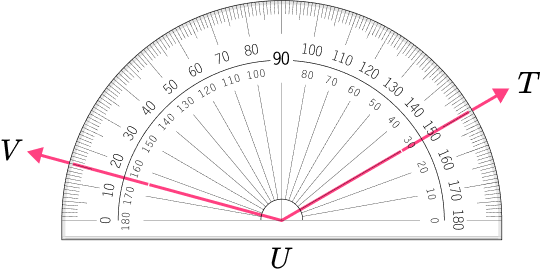
The angle is an acute angle because 85^{\circ} is less than 90^{\circ} .
These angles are larger than 90 degrees and appear to be obtuse.
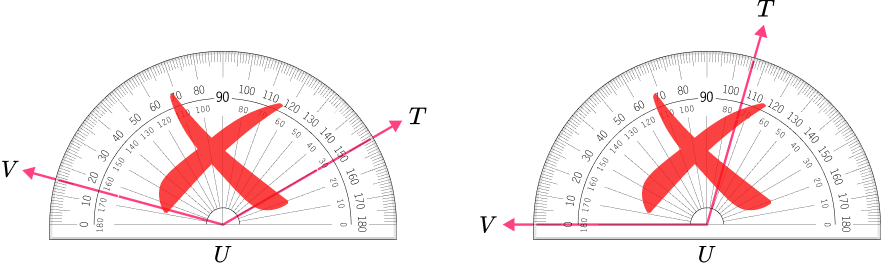
This angle is acute, however, the measure is less than 85 degrees.
This angle shows a measure of 85 degrees because the point V is on 0 degrees and point T is on 85 degrees.
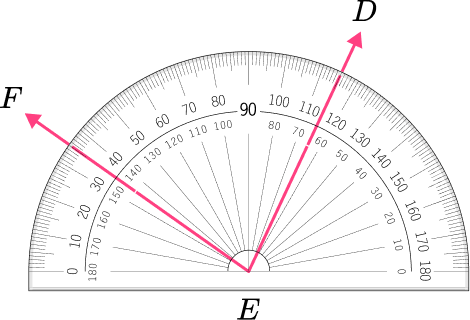
3. What is the measure of angle EFG to the nearest degree?
The vertex is placed correctly on the protractor and the arm is lined up correctly on the bottom of the protractor.
The angle is an acute angle because it appears to be less than 90^{\circ} .
The other arm goes through the 125^{\circ} and 55^{\circ} . Since the angle is acute, the correct measure is 55^{\circ} .
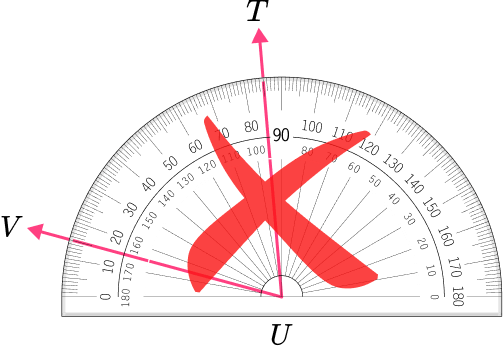
4. Which angle has a measure closest to 115^{\circ} ?
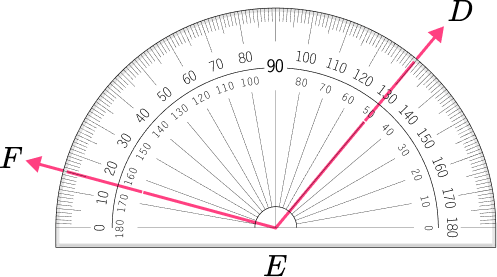
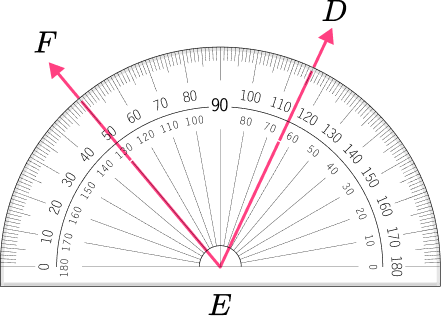
The angle is an obtuse angle because 115^{\circ} is greater than 90^{\circ} .
These angles are smaller than 90 degrees and appear to be acute.
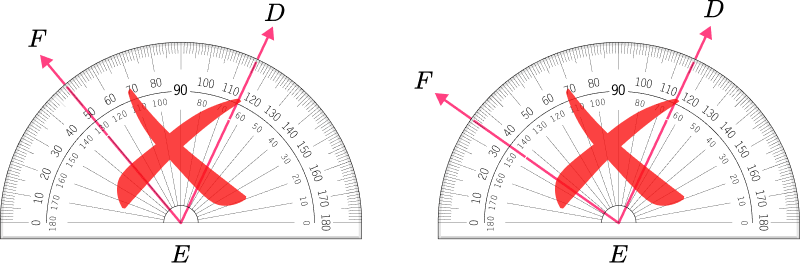
This angle is a straight angle, measuring 180 degrees.
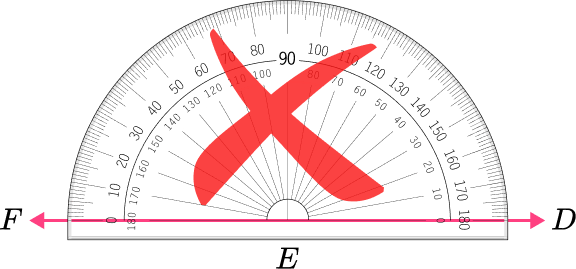
This angle shows a measure of 115 degrees because the point F is on 15 degrees and point D is on 130 degrees. 130-15=115 degrees.
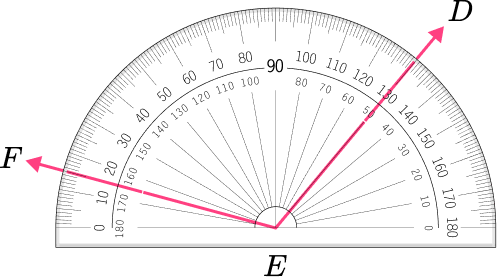
5. What is the measure of angle XYZ to the nearest degree?
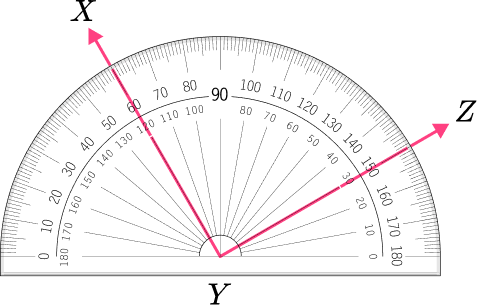
The angle is a right angle because it appears to be exactly 90^{\circ} .
Using the measures that run from left to right, the arm at point X goes through 60^{\circ} , and the arm at point C goes through 150^{\circ} .
Subtract the two measures,
150-60=90
The measure of angle XYZ is 90^{\circ} .
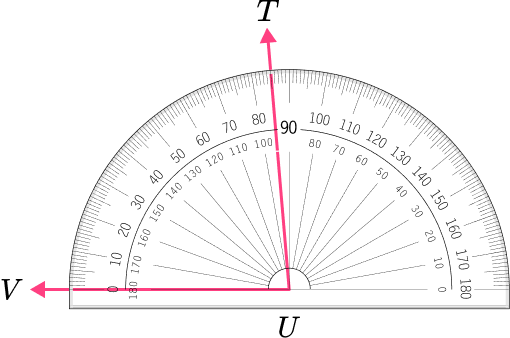
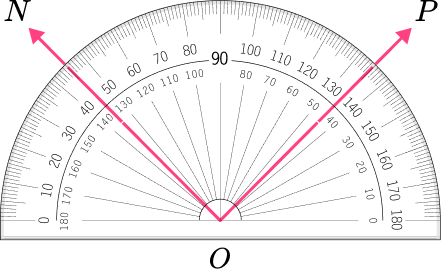
6. Which angle has a measure closest to 90^{\circ} ?
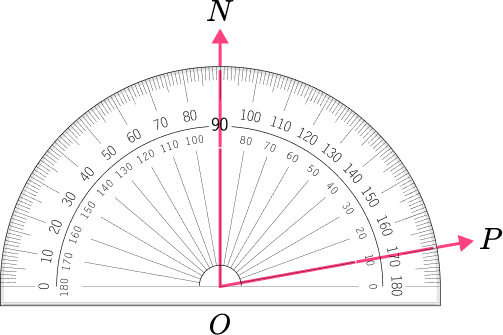
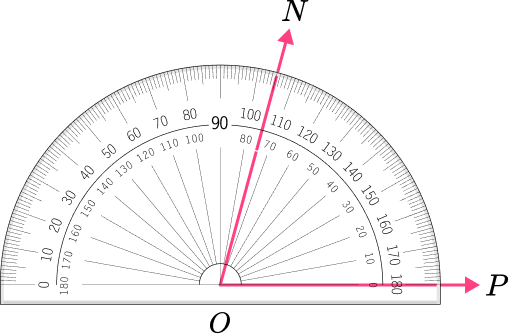
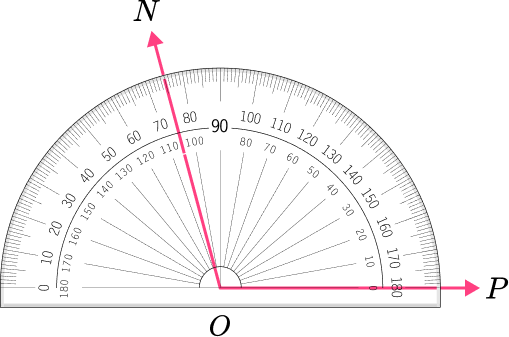
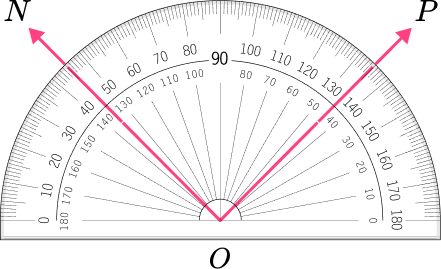
The angle is a right angle because it is equal to 90^{\circ} .
These angles appear to be acute.
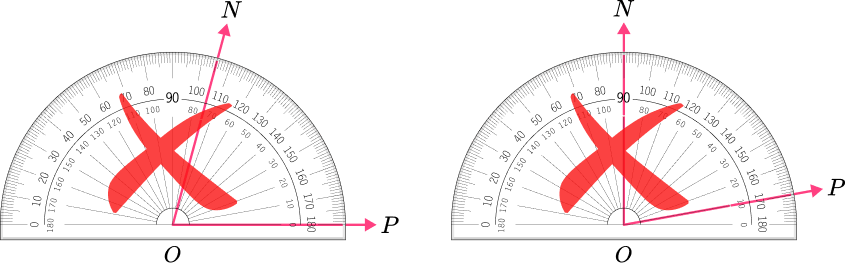
This angle appears to be obtuse.
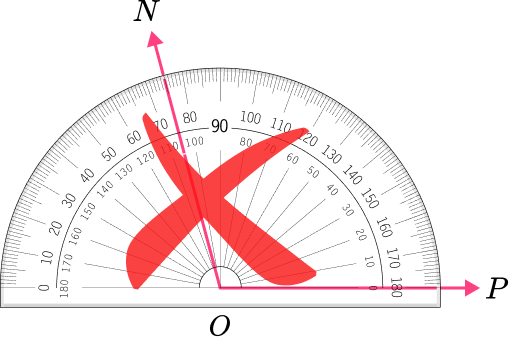
This angle shows a measure of 90 degrees because point N is on 45 degrees and point P is on 135 degrees. 135-45=90 degrees.
Measuring angles FAQs
A straight angle is an angle that measures 180 degrees. A straight angle and a straight line are the same.
A standard protractor can measure up to a 180 degree angle. To measure an angle over 180 degrees, you can measure the angle in smaller parts, and then subtract the total from 360 degrees.
No, the degrees of an angle can involve both fractions and decimals.
Yes, you are able to measure the angles of different polygons. For example, the sum of the interior angles of a triangle is 180 degrees, and the sum of the interior angles of a quadrilateral is 360 degrees.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!