Complementary Angles - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Types of angles Right angle Measuring angles

Math resources Geometry Angles

Complementary angles

Here you will learn about complementary angles, including how to find missing angles by applying knowledge of complementary angles.

Students will first learn about complementary angles as a part of measurement and data in 4th grade. They will expand that knowledge as they progress through middle school.

What are complementary angles?

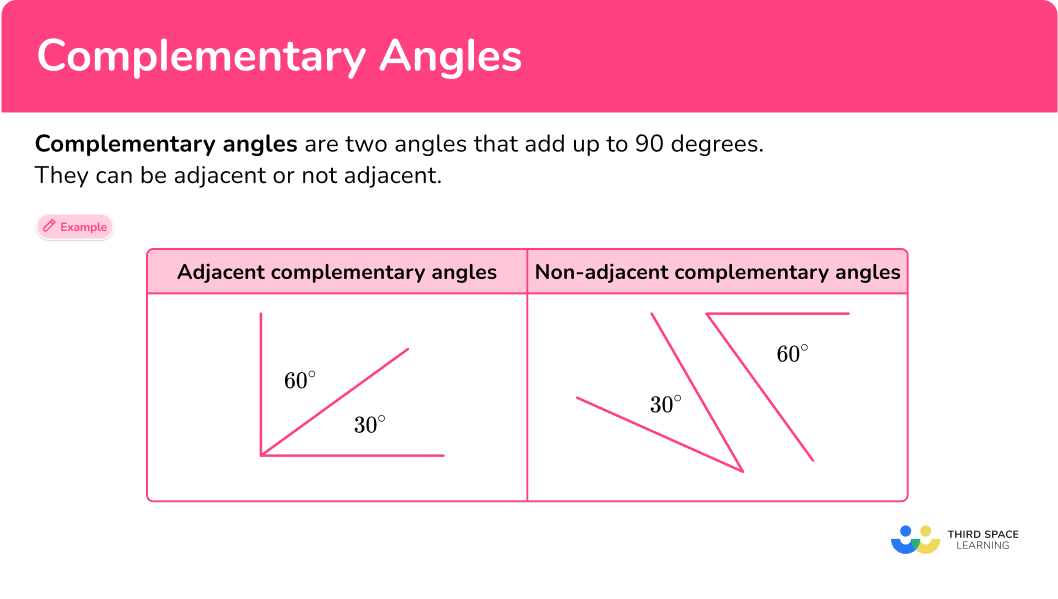
Complementary angles are two angles that add up to $90$ degrees. They can be adjacent or not adjacent. Adjacent angles are angles that share a common arm and a vertex.

Adjacent complementary angles	Non-adjacent complementary angles

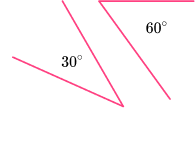Adjacent complementary angles make a right angle.

You can use what you know about complementary angles to decompose angles and find the measurement of an unknown angle.

What are complementary angles?

Common Core State Standards

How does this relate to 4th grade math?

Grade 4: Measurement and Data (4.MD.C.7)
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts.

Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, for example, by using an equation with a symbol for the unknown angle measure.

How to find the measure of complementary angles

In order to find the measure of complementary angles you need to:

Determine which angles are complementary.
Identify given angle measurements and the unknown angle.
Find the missing angle.
Clearly state the answer.

[FREE] Angles Check for Understanding Quiz (Grade 4)

Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Angles Check for Understanding Quiz (Grade 4)

Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

DOWNLOAD FREE

Complementary angles examples

Example 1: finding complementary angles (adjacent angles)

The two angles shown, $x$ and $y,$ are complementary. Find the measure of angle $x.$

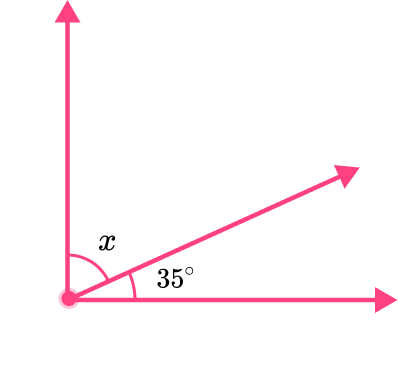
Determine which angles are complementary.

The question states that angles $x$ and $y$ are complementary and equal $90^{\circ}.$

$x+y=90$

2Identify given angle measurements and the unknown angle or angles.

Angle $y$ is $35^{\circ}.$

The unknown angle is angle $x,$ and when it’s added to $35^{\circ}$ will equal $90^{\circ}.$

$x+35=90$

3Find the missing angle.

To find the missing angle, you will subtract $35$ from $90.$

$x=90-35$

$x =55$

4Clearly state the answer.

The measurement of angle $x$ is $55^{\circ}.$

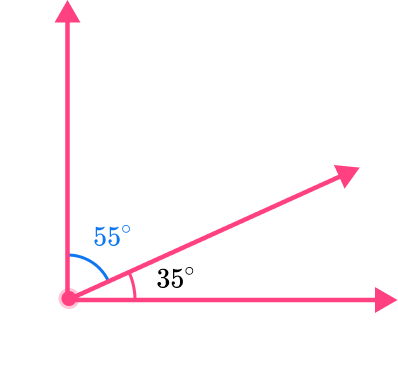
Example 2: finding complementary angles (adjacent angles)

The two angles shown are complementary. Find the measure of angle $x.$

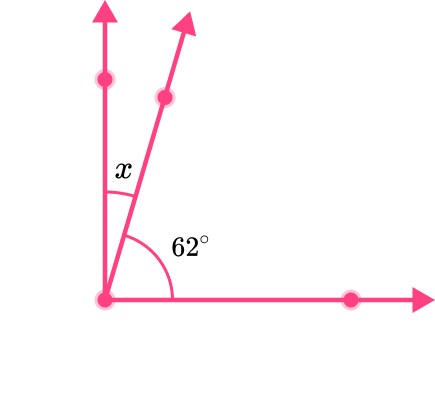
Determine which angles are complementary.

The question states that angles $x$ and $y$ are complementary and equal $90^{\circ}.$

$x+y=90$

Identify given angle measurements and the unknown angle or angles.

Angle $y$ is $62^{\circ}.$

The unknown angle is angle $x,$ and when it’s added to $62^{\circ}$ will equal $90^{\circ}.$

$x+62=90$

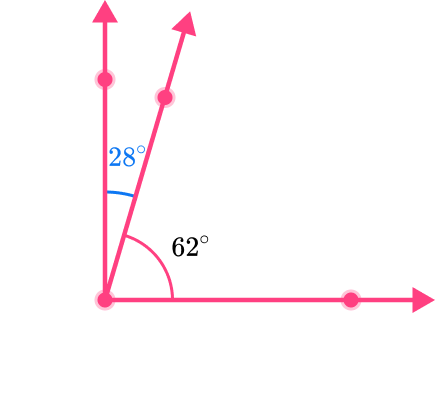
Find the missing angle.

To find the missing angle, you will subtract $62$ from $90.$

$x=90-62$

$x =28$

Clearly state the answer.

The measurement of angle $x$ is $28^{\circ}.$

Example 3: finding complementary angles (not adjacent angles)

The two angles shown are complementary. Find the measure of angle $a.$

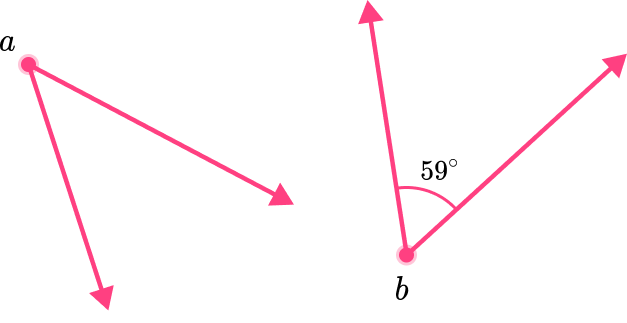
Determine which angles are complementary.

The question states that angles $a$ and $b$ are complementary and equal $90^{\circ}.$

$a+b=90$

Identify given angle measurements and the unknown angle or angles.

Angle $b$ is $59^{\circ}.$

The unknown angle is angle $a,$ and when it’s added to $59^{\circ}$ will equal $90^{\circ}.$

$a+59=90$

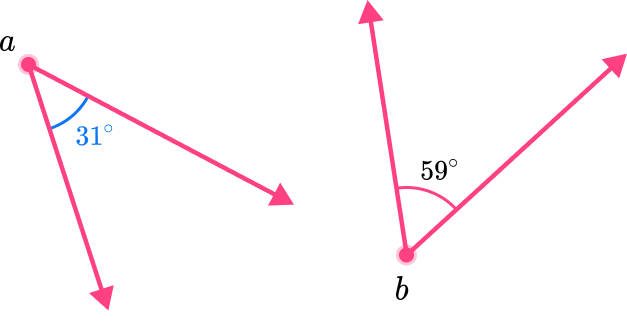
Find the missing angle.

To find the missing angle, you will subtract $59$ from $90.$

$a=90-59$

$a =31$

Clearly state the answer.

The measurement of angle $a$ is $31^{\circ}.$

Example 4: finding complementary angles (not adjacent angles)

The two angles shown are complementary. Find the measure of angle $c.$

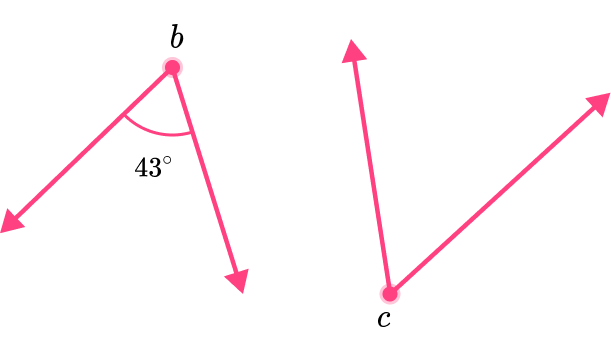
Determine which angles are complementary.

The question states that angles $b$ and $c$ are complementary and equal $90^{\circ}.$

$b+c=90$

Identify given angle measurements and the unknown angle or angles.

Angle $b$ is $43^{\circ}.$

The unknown angle is angle $c,$ and when it’s added to $43^{\circ}$ will equal $90^{\circ}.$

$43+c=90$

Find the missing angle.

To find the missing angle, you will subtract $43$ from $90.$

$c=90-43$

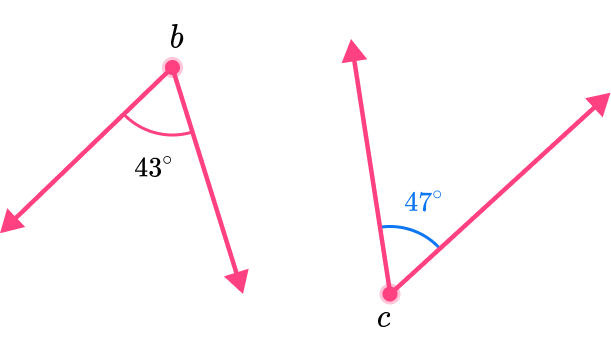
$c =47$

Clearly state the answer.

The measurement of angle $c$ is $47^{\circ}.$

Example 5: finding an angle which is complementary to another

Two angles $‘x$ and $y'$ are complementary and one of them is $49^{\circ}.$ What is the size of the other angle?

Determine which angles are complementary.

The two angles are complementary and therefore equal $90^{\circ}.$

$x+y=90$

Identify given angle measurements and the unknown angle or angles.

Because it is not stated which angle is $49^{\circ},$ you can assume that $\angle x$ has a measure of $49^{\circ}.$

$49^{\circ}+y=90^{\circ}$

Find the missing angle.

You will subtract $49$ from $90$ to find the measure of the missing angle.

$y=90-49$

$y=41^{\circ}$

Clearly state the answer.

The size of the other angle is $41^{\circ}.$

Example 6: finding an angle which is complementary to another

Two angles $‘x$ and $y'$ are complementary and one of them is $17^{\circ}.$ What is the size of the other angle?

Determine which angles are complementary.

The two angles are complementary and therefore equal $90^{\circ}.$

$x+y=90$

Identify given angle measurements and the unknown angle or angles.

Because it is not stated which angle is $17^{\circ},$ you can assume that $\angle x$ has a measure of $17^{\circ}.$

$17^{\circ}+y=90^{\circ}$

Find the missing angle.

You will subtract $17$ from $90$ to find the measure of the missing angle.

$y=90-17$

$y=73^{\circ}$

Clearly state the answer.

The size of the other angle is $73^{\circ}.$

Teaching tips for complementary angles

Rather than having students practice finding and decomposing complementary angles on multiple skill worksheets, provide them with a variety of practice problems, activities, and/or projects that have a real-world context. This will deepen their understanding of this skill.

Easy mistakes to make

Mixing up supplementary angles and complementary angles
Students may mix up supplementary and complementary angles, thinking that complementary angles add up to $180^{\circ}$ and that supplementary angles add up to $90^{\circ}.$ However, complementary angles add up to $90^{\circ}$ and supplementary angles add up to $180^{\circ}.$

Assuming complementary angles always have a common vertex
Complementary angles can be either adjacent or not adjacent. Not adjacent complementary angles do not share a common vertex, but their angles will still add up to $180^{\circ}.$

Angles
Acute angle
Obtuse angle
Adjacent angles
Supplementary angles
Geometry theorems
Vertical angle theorem
Straight angle
Angles point
Pentagon angles

Complementary angles practice questions

m=61^{\circ}

m=161^{\circ}

m=154^{\circ}

m=71^{\circ}

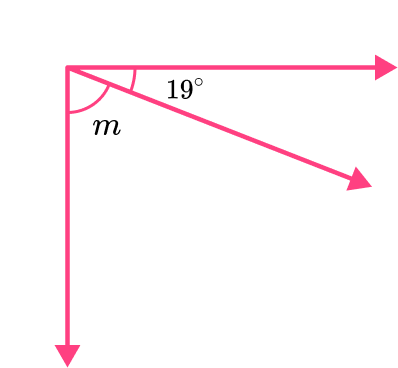
The two angles are complementary, so they must have a sum of $90.$

You will subtract $19$ from $90$ to find the measure of the missing angle.

$m=90-19$

$m=71$

The missing angle measures at $71^{\circ}.$

k=43^{\circ}

k=45^{\circ}

k=145^{\circ}

k=143^{\circ}

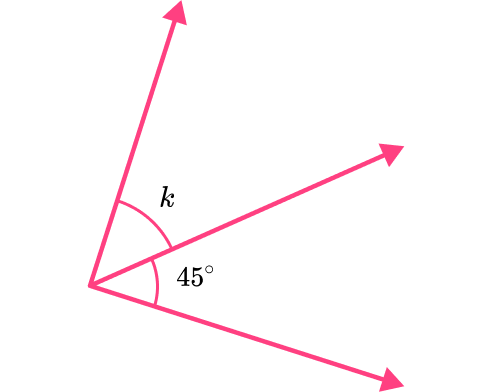
The two angles are complementary, so they must have a sum of $90.$

You will subtract $45$ from $90$ to find the measure of the missing angle.

$k=90-45$

$k=45$

The missing angle measures at $45^{\circ}.$

w=154^{\circ}

w=47^{\circ}

w=54^{\circ}

w=132^{\circ}

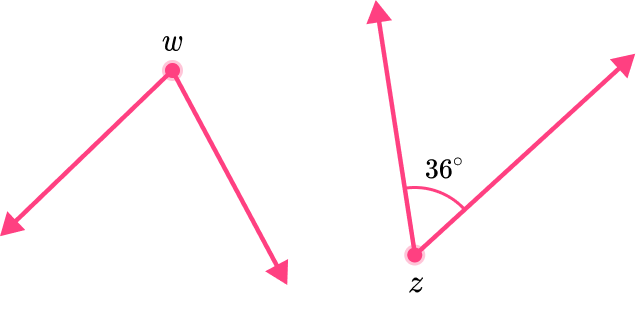
The two angles are complementary, so they must have a sum of $90.$

You will subtract $36$ from $90$ to find the measure of the missing angle.

$w=90-36$

$w=54$

The missing angle measures at $54^{\circ}.$

e=123^{\circ}

e=90^{\circ}

e=44^{\circ}

e=24^{\circ}

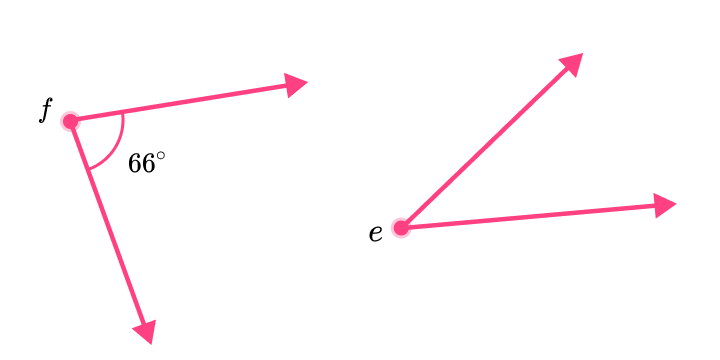
The two angles are complementary, so they must have a sum of $90.$

You will subtract $66$ from $90$ to find the measure of the missing angle.

$e=90-66$

$e=24$

The missing angle measures at $24^{\circ}.$

x=33^{\circ}

x=43^{\circ}

x=133^{\circ}

x=313^{\circ}

The two angles are complementary, so they must have a sum of $90.$

You will subtract $47$ from $90$ to find the measure of the missing angle.

$x=90-47$

$x=43$

The missing angle measures at $43^{\circ}.$

x=87^{\circ}

x=3^{\circ}

x=93^{\circ}

x=177^{\circ}

The two angles are complementary, so they must have a sum of $90.$

You will subtract $3$ from $90$ to find the measure of the missing angle.

$x=90-3$

$x=87$

The missing angle measures at $87^{\circ}.$

Complementary angles FAQs

What is the definition of complementary angles?

Two angles that add up to $90$ degrees and can be adjacent or not adjacent.

What’s the difference between complementary and supplementary angles?

Complementary angles add up to $90$ degrees, or a right angle.
Supplementary angles add up to $180$ degrees, or a straight line or straight angle.

Can three angles be complementary?

No, three angles will never be complementary, even if the sum of their measurement is $90^{\circ}.$ You will only see a pair of complementary angles.

Is there a formula for complementary angles?

$\angle a+ \angle b=90^{\circ};$ two angles are complementary if $angle \, a$ and $angle \, b$ equal $90^{\circ}.$

The next lessons are

Angles in parallel lines
Triangles
2D shapes
Lines

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.