High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Types of angles Acute angles Obtuse angles Right angles Adjacent angles Combining like termsStraight angle
Here we will learn about straight angles, including the sum of straight angles, how to find missing angles, and using these angle facts to generate equations and solve problems.
Students will first learn about straight angles as part of geometry in 7 th grade.
What are straight angles?
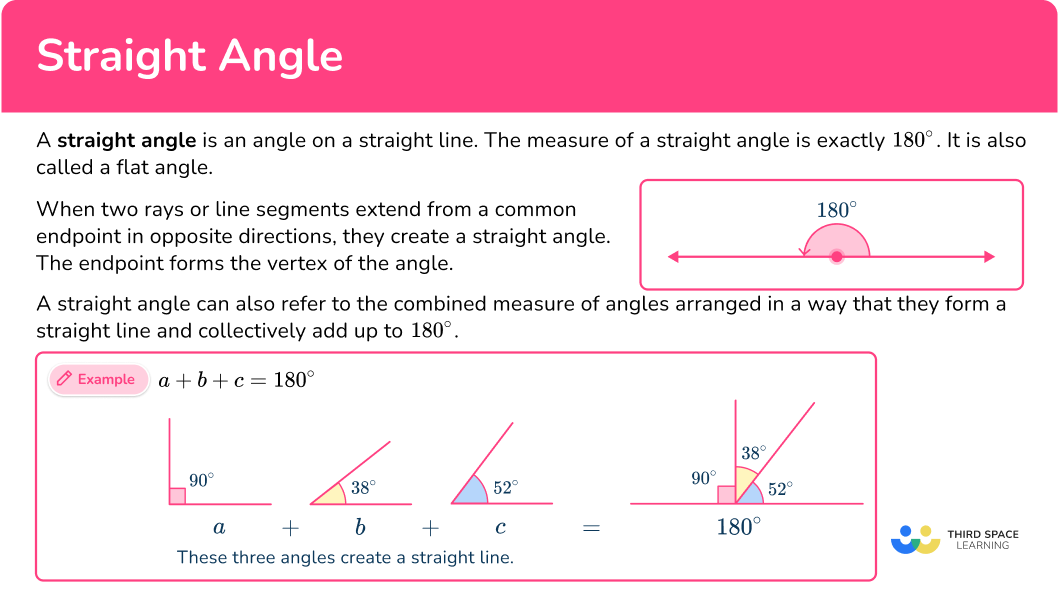
A straight angle is an angle on a straight line. The measure of a straight angle is exactly 180^{\circ}. It is also called a flat angle.
When two rays or line segments extend from a common endpoint in opposite directions, they create a straight angle. The endpoint forms the vertex of the angle.

A straight angle can also refer to the combined measure of angles arranged in a way that they form a straight line and collectively add up to 180^{\circ}.
For example, let’s take the three angles of a, b, and c.
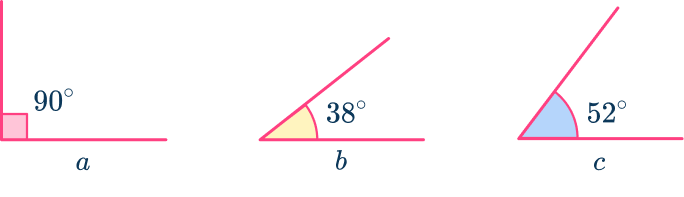
If we move these three angles so that each vertex meets, we get an arrangement that looks like this:
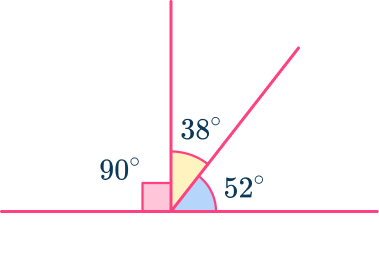
These three angles create a straight line.
By adding together a=90^{\circ}, b=38^{\circ} and c=52^{\circ}, we can see the angle measurements add up to 180^{\circ}. Therefore, they create a straight angle.
What are straight angles?
Common Core State Standards
How does this relate to 7 th grade math?
- Grade 7 – Geometry (7.G.B.5)
Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Worksheet (Grade 4)
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Worksheet (Grade 4)
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREEHow to find missing angle measurements on a straight angle
In order to find missing angle measurements on a straight angle:
- Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
- Simplify by collecting like terms.
- Solve the equation.
Straight angle examples
Example 1: obtuse angle
The angles below create a linear pair, which is a pair of angles that form a straight line. Calculate the missing angle x.
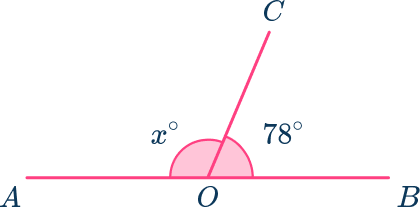
- Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
2Simplify by collecting like terms.
Here, there are no terms to collect without solving the equation.
3Solve the equation.
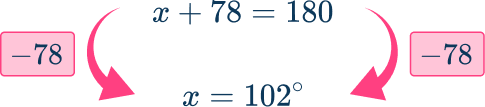
Example 2: acute angle
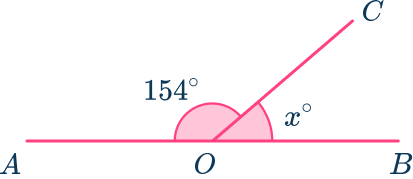
AB is a straight line through O. Calculate the missing angle x.
Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
Simplify by collecting like terms.
Here, there are no terms to collect without solving the equation.
Solve the equation.
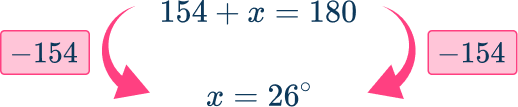
Example 3: right angle
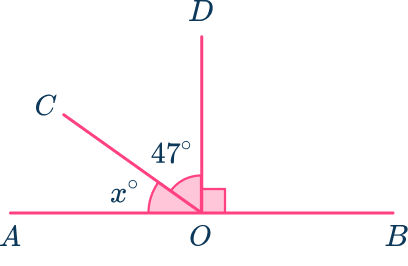
AB is a straight line through O. Calculate the missing angle x.
Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
Simplify by collecting like terms.
Solve the equation.
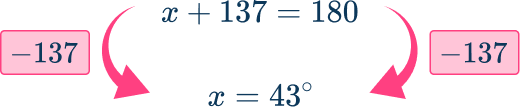
Example 4: vertically opposite angles
AB and CD are straight lines. By calculating the value of y, determine the value of x.
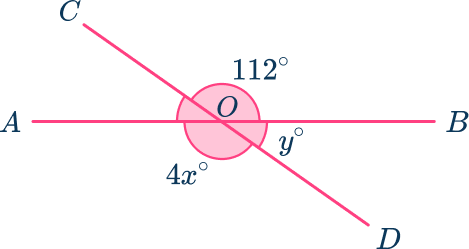
Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
First, you need to calculate the value of y and use this to form an equation to calculate the value of x. As straight angles sum to 180^{\circ},
Now, 4x+y=180. As y=68, you need to solve the equation
4x+68=180
Simplify by collecting like terms.
Here, there are no terms to collect without solving the equation.
Solve the equation.
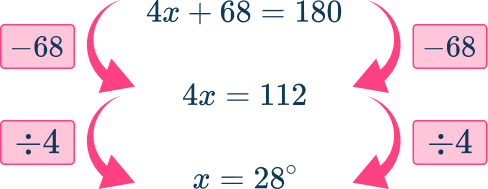
Note, for this example, you could have used the angle fact: vertically opposite angles are equal to show that 4x=112 and so x=28^{\circ}.
Example 5: forming and solving equations
AB is a straight line through O. Calculate the size of all the angles that make up the line AB.
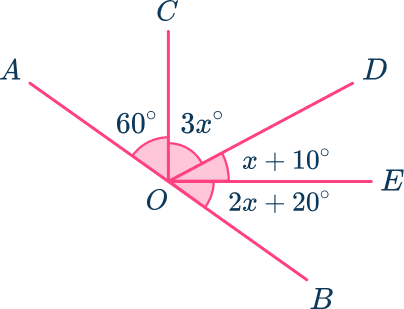
Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
Simplify by collecting like terms.
Collect the x terms: 3x+x+2x=6x
Collect the numerical terms: 60+10+20=90
The simplified equation is 6x+90=180.
Solve the equation.
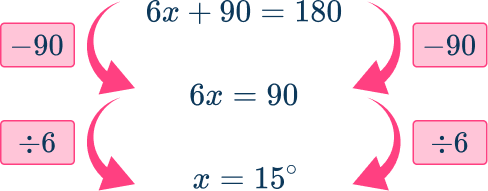
As x=15, substitute this into each angle to find their values:
We can check the solution by adding up the angles:
60+45+25+50=180^{\circ}
Example 6: circles and tangents
AB is a tangent to the circle with center C. The tangent intersects the circle at the point O on the circumference. Use this information to calculate the value of x.
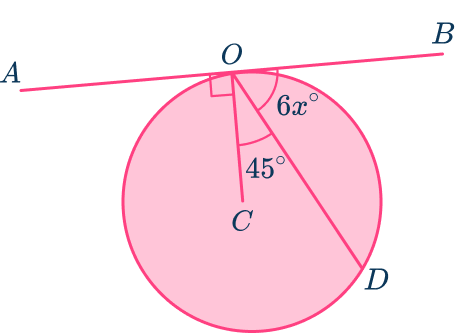
Form an equation using the rule: The sum of angles in a straight angle =\bf{180^{\circ}}.
Simplify by collecting like terms.
Now, 6x+135=180
Solve the equation.
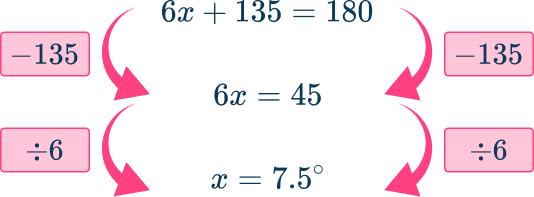
Note, for this example, you could have used the angle fact: the sum of angles in a right angle is 90^{\circ} to show that 6x+45=90 and so x=7.5^{\circ}.
Teaching tips for straight angles
- Show real life examples of straight angles, like the edges of a book or the arms of a clock at 6 o’clock.
- Build upon students’ prior knowledge of angles, such as right angles and acute angles, to introduce straight angles. Highlight how straight angles relate to different types of angles they have previously learned about.
- Use formative assessment strategies such as exit tickets, multiple choice quizzes, or mini whiteboard activities to gauge student understanding of straight angles. Provide immediate feedback on worksheets during class to address misconceptions and reinforce key concepts.
Easy mistakes to make
- Thinking that the sum of straight angles is equal to \bf{360^{\circ}}
Some students may incorrectly remember straight angles as 360^{\circ}, rather than 180^{\circ}. The sum of straight angles is half of a revolution, which is 180^{\circ}.
- Using a protractor
When you are asked to calculate a missing angle, a common error is to use a protractor to measure the angle. When using angle facts to determine angles, diagrams are deliberately not drawn to scale unless it is a 90 degree angle or a 180 degree angle as these are important angles to recognize. You should not use a protractor for this style of question.
- Confusing straight angles with reflex angles
Students might confuse straight angles with reflex angles, which are angles greater than 180^{\circ} and less than 360^{\circ}.
Related angles lessons
- Measuring angles
- Supplementary angles
- Complementary angles
- Geometry theorems
- Vertical angle theorems
- Angles point
- Pentagon angles
Practice straight angles questions
1. The two angles shown below form a linear pair. Calculate the size of angle x.





2. AOB is a straight line. Calculate the size of angle x.
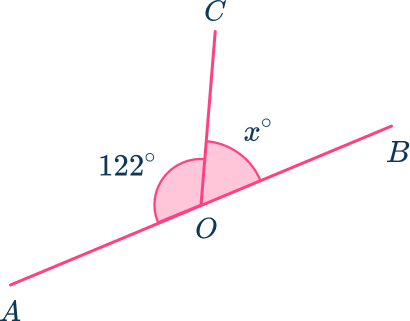




3. Calculate the size of the angle 2x. Hence find the value of x.
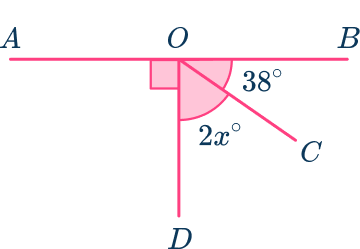




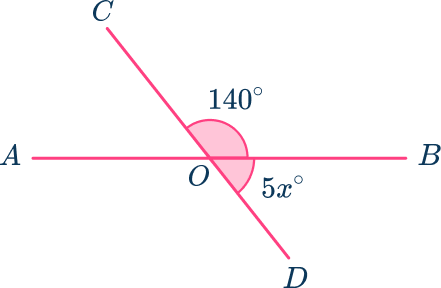
4. AB and CD are straight lines. Calculate the size of angle BOD. Hence find the value of x.




5. AOB is a straight line. By finding the value for x, calculate the size of each angle in the diagram below.
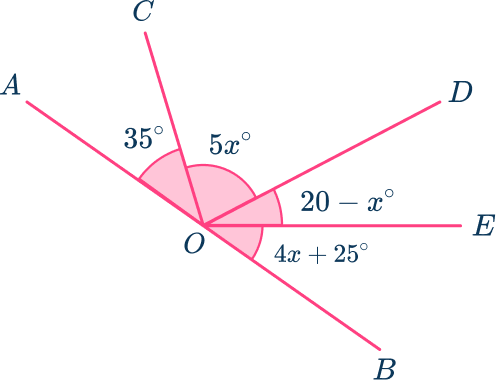




\begin{aligned}8x+80&=180 \\\\ 8x&=180-80 \\\\ 8x&=100 \\\\ x&=100\div{8} \\\\ x&=12.5^{\circ} \end{aligned}
5x=5\times{12.5}=62.5^{\circ}
20-x=20-12.5=7.5^{\circ}
4x+25=4\times{12.5}+25=75^{\circ}
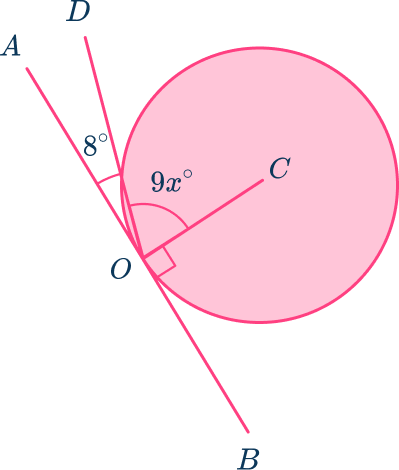
6. The circle with center C has a tangent at point O. Calculate the value of x correct to the nearest hundredth ( 2 decimal places).




Straight angle FAQs
A straight angle is an angle on a straight line whose measure is exactly 180^{\circ}. It is also called a flat angle.
A straight angle is a specific type of angle that measures 180^{\circ} (or radians) and forms a straight line. Supplementary angles are angle pairs whose measures add up to 180^{\circ} but they don’t have to form a straight line. They can be adjacent or non-adjacent angles.
A straight angle measures 180^{\circ} while a full angle, or a complete angle, measures 360^{\circ}. Two straight angles equal one full angle.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!