Adjacent Angles - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Angles Types of angles

Math resources Geometry Angles

Adjacent angles

Here you will learn about adjacent angles, including how to identify adjacent angles and examples of adjacent angles.

Students will first learn about adjacent angles as part of geometry and measurement and data in $4$ th grade.

What are adjacent angles?

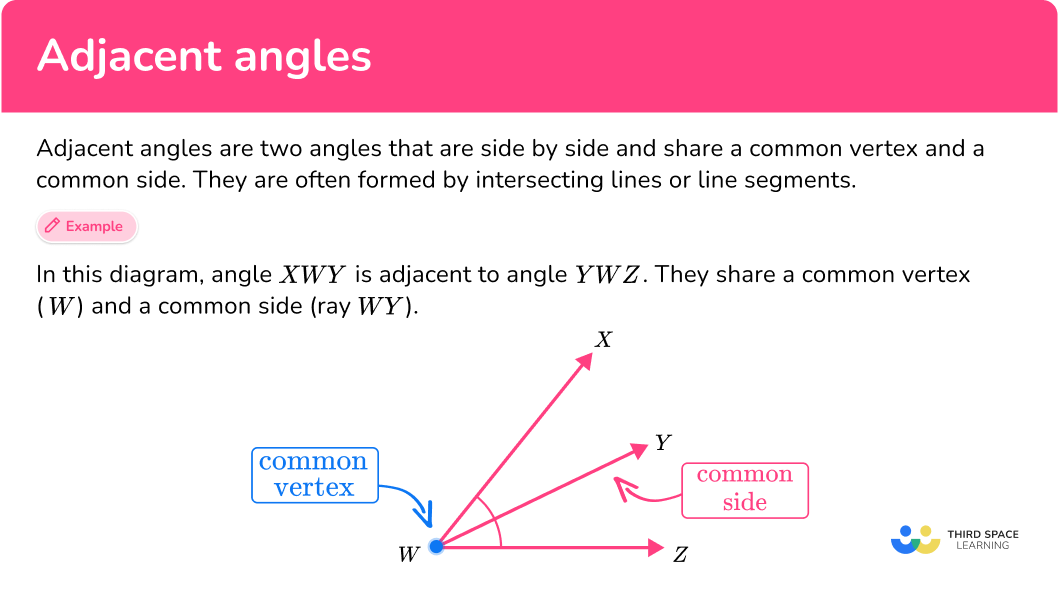
Adjacent angles are two angles that are side by side and share a common vertex and a common side. They are often formed by intersecting lines or line segments.

Since an angle is formed when two rays meet at a common endpoint, adjacent angles are simply two angles that are directly next to each other. Adjacent angles can be complementary angles or supplementary angles.

For example, in this diagram, angle $XWY$ is adjacent to angle $YWZ$ . They share a common vertex ( $W$ ) and a common side (ray $WY$ ).

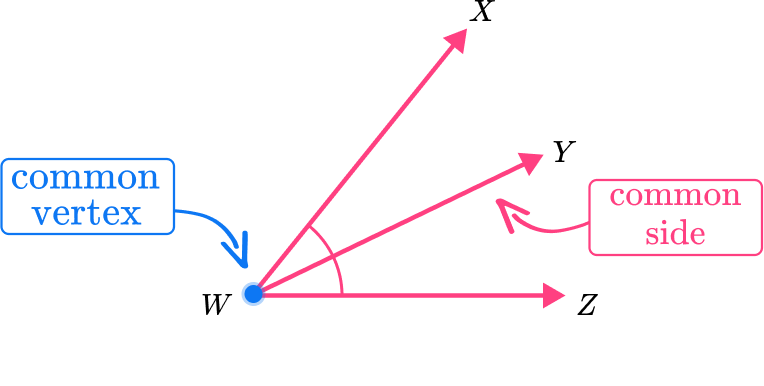
Types of angles

A linear pair is a pair of adjacent angles that combine to form a straight angle. The angles in a linear pair are supplementary angles, meaning their measures add up to $180^{\circ}.$

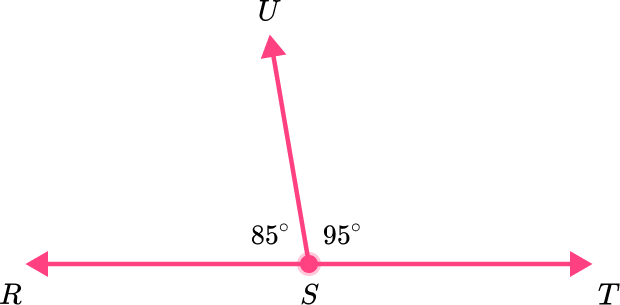
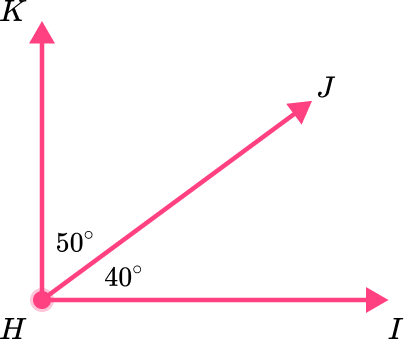
Adjacent angles can also be complementary angles. Complementary adjacent angles are angles that add up to $90^{\circ}$ .

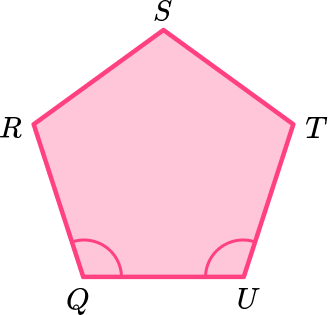
Adjacent angles can also be found within the interior angles of polygons.

For example, one pair of adjacent angles in the pentagon is angle $RQU$ and angle $QUT$ .

What is adjacent angles?

Common Core State Standards

How does this relate to 4th grade math?

Grade 4 – Geometry (4.G.A.1)
Draw points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. Identify these in two-dimensional figures.

Grade 4 – Geometry (4.MD.C.7)
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, for example, by using an equation with a symbol for the unknown angle measure.

How to identify adjacent angles

In order to identify adjacent angles:

Recall the definition of adjacent angles.
Determine which angles are adjacent and name them.

[FREE] Adjacent Angles Worksheet (Grade 4 to 5)

Use this worksheet to check your grade 4 to 5 students’ understanding of adjacent angles. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Adjacent Angles Worksheet (Grade 4 to 5)

Use this worksheet to check your grade 4 to 5 students’ understanding of adjacent angles. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Adjacent angles examples

Example 1: identify adjacent angles

Name the pair of adjacent angles.

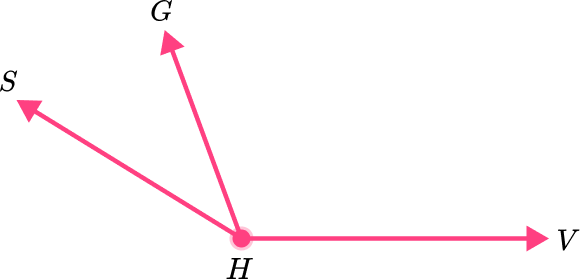
Recall the definition of adjacent angles.

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

2Determine which angles are adjacent and name them.

Angle $SHG$ and angle $GHV$ are adjacent angles.

Example 2: identify adjacent angles

Name the acute angle that is adjacent to angle $QPE$ .

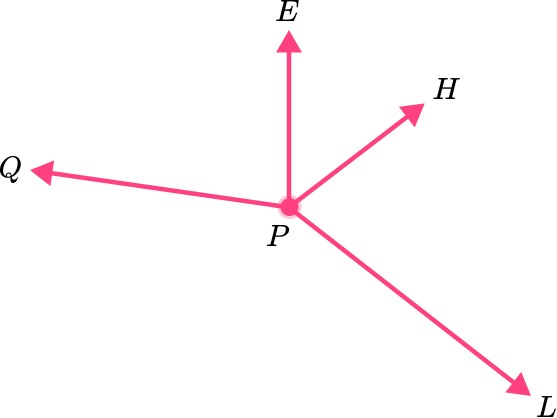
Recall the definition of adjacent angles.

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

Determine which angles are adjacent and name them.

Angle $EPH$ is adjacent to angle $QPE$ .

Example 3: identify multiple pairs of adjacent angles

Name $2$ pairs of adjacent angles.

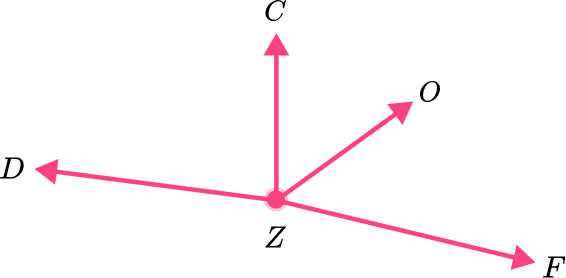
Recall the definition of adjacent angles.

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

Determine which angles are adjacent and name them.

Any angles that share a common vertex and a common side are adjacent angles. For example, angle $DZC$ and angle $CZO$ are one pair of adjacent angles. Another pair of adjacent angles is angle $CZO$ and angle $OZF$ .

Example 4: identify adjacent angles in real world objects

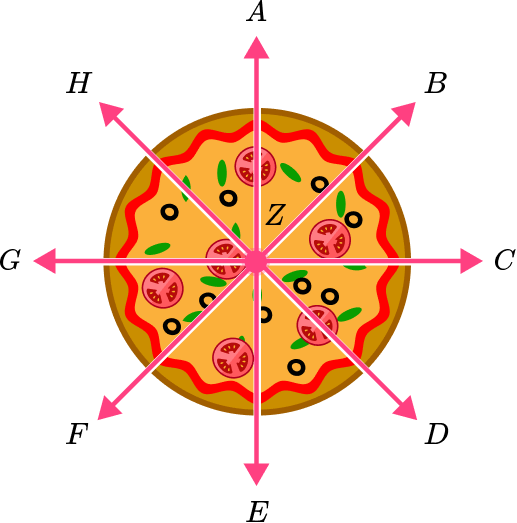
Find two pairs of adjacent angles in the pizza.

Recall the definition of adjacent angles.

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

Determine which angles are adjacent and name them.

Any angles that share a common vertex and a common side are adjacent angles. For example, one pair of adjacent angles in the pizza is angle $CZD$ and angle $DZE$ . Another pair of adjacent angles is angle $GZH$ and angle $HZA$ .

How to find a missing angle measure within adjacent angles

In order to find a missing angle measure within adjacent angles:

Recall the definition of adjacent angles.
Determine which angles are adjacent and name them.
Subtract the known angle measure from the total angle measure of the adjacent angles.

Example 5: find the missing angle measure.

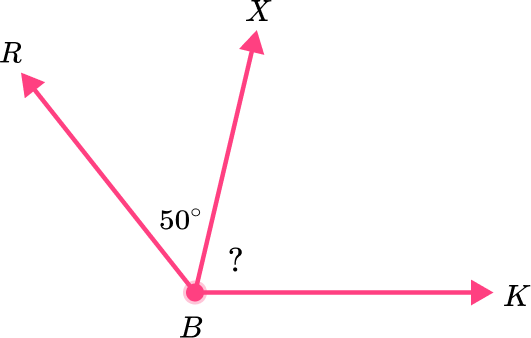
The total angle measure of the adjacent angles is $130^{\circ}$ . What is the measure of angle $XBK?$

Recall the definition of adjacent angles.

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

Determine which angles are adjacent and name them.

The adjacent angles are angle $RBX$ and angle $BXK$ .

Subtract the known angle measure from the total angle measure of the adjacent angles.

Total angle measure = $130^{\circ}$ .

Known angle measure (angle $RBX$ ) = $50^{\circ}$

$130^{\circ}-50^{\circ} = 80^{\circ}$

So the missing angle measure (angle $BXK$ ) is $80^{\circ}$ .

Example 6: find the missing angle measure in a linear pair of angles.

A linear pair of angles is a pair of adjacent angles that add up to $180^{\circ}$ . They are also supplementary angles.

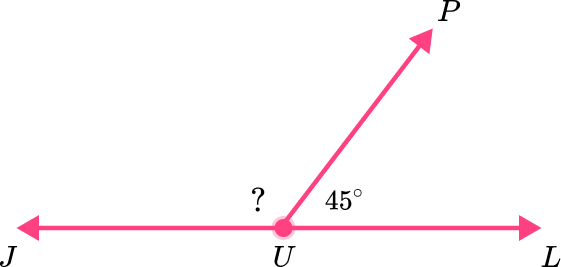
What is the measure of angle $JUP?$

Recall the definition of adjacent angles.

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

Determine which angles are adjacent and name them.

The adjacent angles are angle $JUP$ and angle $PUL$ .

Subtract the known angle measure from the total angle measure of the adjacent angles.

Total angle measure = $180^{\circ}$ .

Known angle measure (angle $PUL$ ) = $45^{\circ}$

$180^{\circ}-45^{\circ} = 135^{\circ}$

So the missing angle measure (angle $JUP$ ) is $135^{\circ}$ .

Teaching tips for adjacent angles

Providing real-life examples of adjacent angles (either hands-on or on worksheets) to make the concept more relatable and tangible for students. For instance, you can use classroom objects, such as books or desks.

Incorporate interactive games or online resources that focus on adjacent angles. There are numerous educational websites and apps that provide interactive activities where students can practice identifying, measuring, and classifying adjacent angles.

Easy mistakes to make

Overlapping angles
Students may believe that if two angles overlap partially or fully, they are considered adjacent angles. However, adjacent angles should not overlap; they share a common vertex and a common side but do not intersect.
For example, angle $MLO$ is not adjacent to angle $MLN$ since they overlap.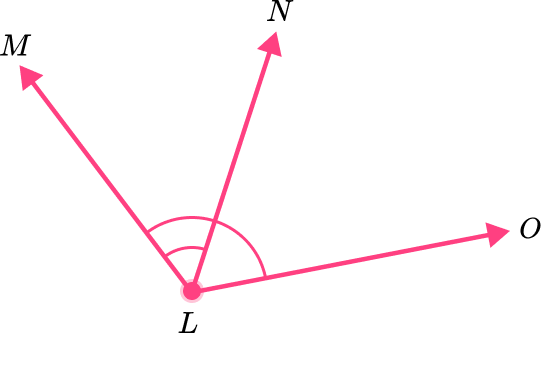

Non-adjacent angles on the same line
Students may confuse non-adjacent angles on the same line as adjacent angles. It’s important to clarify that adjacent angles must have a common vertex and side, meaning they are next to each other.
For example, angle $ABE$ and angle $DBC$ are located on the same straight line, but they are not adjacent angles since they are not next to each other.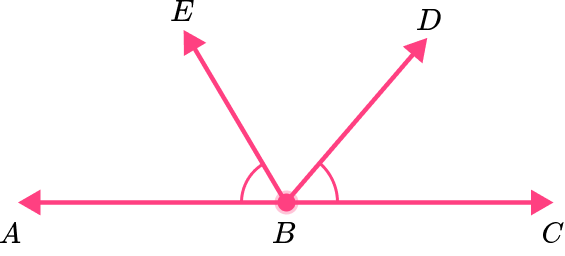

Related angles lessons

Angles
Acute angle
Obtuse angle
Types of angles
Right angle
Measuring angles
Complementary angles
Supplementary angles
Geometry theorems
Vertical angle theorem
Straight angle
Angles point
Pentagon angles

Practice adjacent angles questions

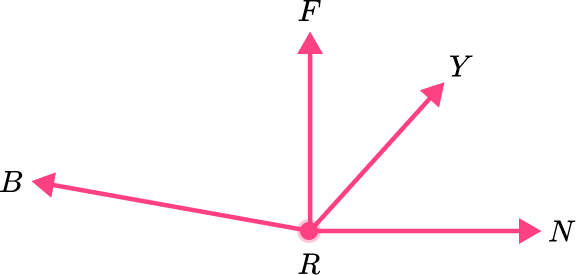
angle $BRF$ and angle $RYN$

angle $FRY$ and angle $YRN$

angle $BRF$ and angle $BRY$

angle $YRN$ and angle $FRN$

Angle $FRY$ and angle $YRN$ are adjacent angles since they are next to each other without overlapping.

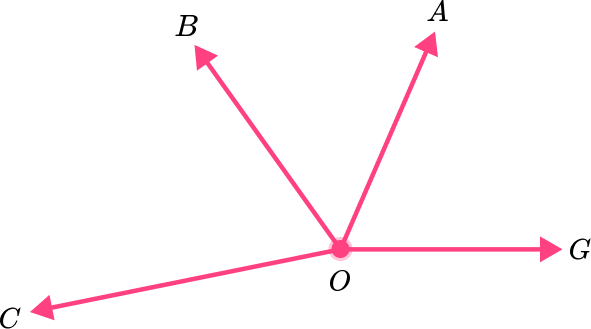
angle $AOG$

angle $COA$

angle $BOA$

angle $BAG$

Angle $BOA$ is right next to angle $COB$ and they do not overlap, so they are adjacent.

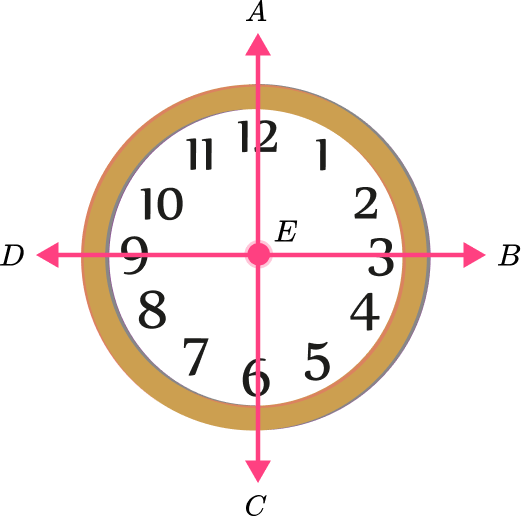
Angles $AEB$ and $AEC$ ; angles $AEB$ and $BEC$

Angles $CED$ and $CEA$ ; angles $DEA$ and $AEB$

Angles $DEB$ and $BED$ ; angles $AEC$ and $BEC$

Angles $BEC$ and $CED$ ; angles $AEB$ and $BEC$

One pair of adjacent angles is angle $BEC$ and angle $CED$ . Another pair is angle $AEB$ and angle $BEC$ . These are the only options in the answer choices where each pair of angles does not overlap.

90^{\circ}

77^{\circ}

167^{\circ}

13^{\circ}

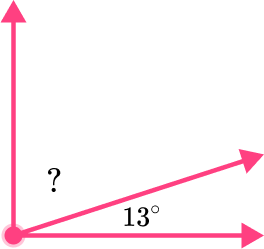
Since you know the total measure of the adjacent angles is $90^{\circ}$ , you can subtract $13^{\circ}$ from $90^{\circ}$ .

$90^{\circ}-13^{\circ}=77^{\circ}$

71^{\circ}

81^{\circ}

180^{\circ}

19^{\circ}

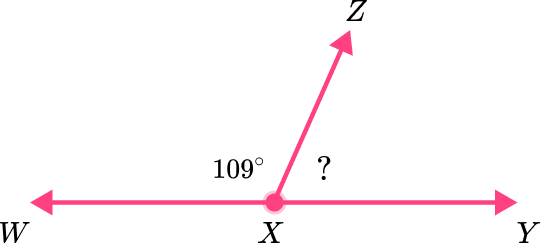
A linear pair is a pair of adjacent angles that combine to form a straight angle. The angles in a linear pair are supplementary angles, meaning their measures add up to $180^{\circ}$ . To calculate the missing angle, we subtract the known angle from the total angle measure of $180^{\circ}$ .

$180^{\circ}-109^{\circ}=71^{\circ}$

Angle $A$ and angle $C$

Angle $C$ and angle $D$

Angle $B$ and angle $D$

There are no adjacent angles in this polygon.

Angle $C$ and angle $D$ are adjacent angles because they are interior angles in a polygon (specifically a rectangle) that are right next to each other. They are also both right angles.

Adjacent angles FAQs

What are adjacent angles?

Adjacent angles are two angles that are side by side and share a common vertex and a common side.

What are the properties of adjacent angles?

The properties of adjacent angles are:
◌ they share a common vertex
◌ they share a common side
◌ they do not overlap
◌ they can be part of a linear pair or have other angle relationships like being complementary or supplementary

What is a linear pair of angles?

A linear pair is a pair of adjacent angles that combine to form a straight angle. The angles in a linear pair are supplementary angles, meaning their measures add up to $180^{\circ}.$

When are adjacent angles complementary angles?

Adjacent angles are complementary when the sum of their measures is equal to $90^{\circ}.$

When are adjacent angles supplementary angles?

Adjacent angles are supplementary when the sum of their measures is equal to $180^{\circ}.$

Can vertical angles be adjacent angles?

No, vertical angles cannot be adjacent angles. Vertical angles are formed when two lines intersect, and they are opposite to each other. Adjacent angles are next to each other.

The next lessons are

Angles in parallel lines
Triangles
2D shapes
Lines

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.