High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
AnglesRight angle
Here is everything you need to know about a right angle, including what it is and how to identify it.
Students first learn about right angles in 4 th grade with their work in geometric measurements. They expand that knowledge as they progress through middle school.
What is a right angle?
A right angle is an angle that is exactly 90^{\circ} .
Right angles are formed when two rays extend from a common point and are perpendicular to each other.
For example,
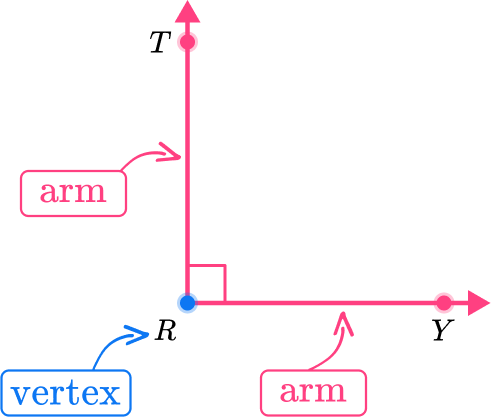
The symbol (\angle) is used to name an angle. The angle can be named after its vertex or the vertex and a point on each ray.
The right angle above can be named \angle \mathrm{R}, \angle \mathrm{TRY} \text { or } \angle \mathrm{YRT} .
A 90^{\circ} angle is often identified with a small square at the vertex. However, if no information is given to identify an angle, measure the angle with a protractor to verify whether it is right or not.
Right angles are also formed when the sides of 2D shapes (polygons) come together.
For example,
This rectangle has four interior right angles.
Some shapes can have interior angles that are right angles and others that are not.
For example,
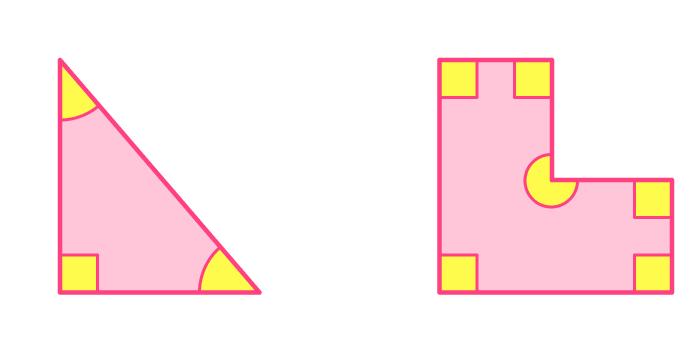
Both the triangle and the irregular pentagon have right angles, but also other angles that are not right.
Right angles can also be formed when two straight lines cross or intersect, and the lines are perpendicular.
For example,
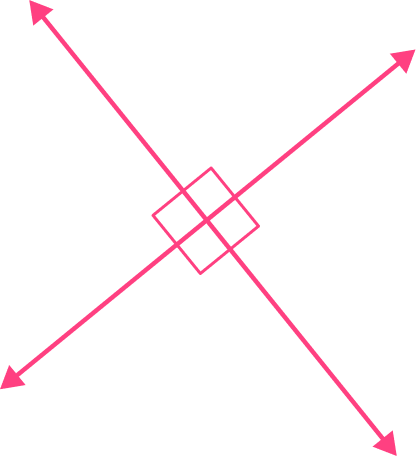
Four right angles are formed when these lines intersect. When lines cross at a 90 -degree angle, they are called perpendicular lines, and each angle formed is a right angle.
What is a right angle?
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Worksheet (Grade 4)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] Angles Worksheet (Grade 4)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 4 th grade math?
- Grade 4 – Measurement and Data (4.MD.C.5.a)
An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through \cfrac{1}{360} \, of a circle is called a “one-degree angle,” and can be used to measure angles.
- Grade 4 – Measurement and Data (4.MD.C.5.b)
An angle that turns through n one-degree angles is said to have an angle measure of n degrees.
- Grade 4 – Measurement and Data (4.MD.C.7)
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, example, by using an equation with a symbol for the unknown angle measure.
- Grade 4 – Geometry (4.G.A.1)
Draw points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. Identify these in two-dimensional figures.
How to identify a right angle
In order to identify a right angle:
- Recall the definition of a right angle.
- Explain whether or not the angle is right.
Right angle examples
Example 1: classify a given angle
Is the angle a right angle?
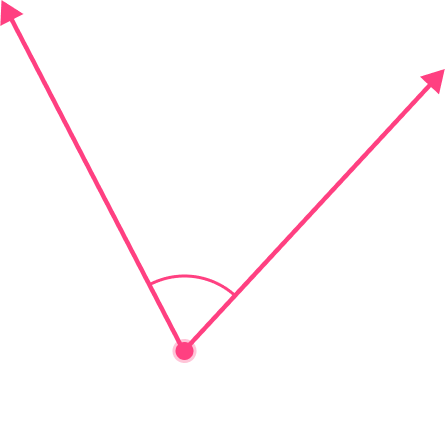
- Recall the definition of a right angle.
A right angle is an angle that is exactly 90^{\circ} .
2Explain whether or not the angle is right.
A right angle aligns perfectly with the corner of a square (shown in blue). This angle is NOT a right angle, because it is less than 90^{\circ} .
Example 2: classify a given angle
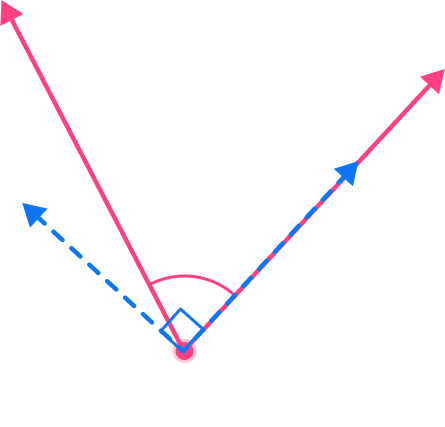
Is the angle a right angle?
Recall the definition of a right angle.
A right angle is an angle that is exactly 90^{\circ} .
Explain whether or not the angle is right.
A right angle aligns perfectly with the corner of a square (shown in blue). This angle is a right angle, because it is exactly 90^{\circ} .
Example 3: identify right angles in a given shape
How many right angles does this shape have?
Recall the definition of a right angle.
A right angle is an angle that is exactly 90^{\circ} .
Explain whether or not the angle is right.
A right angle aligns perfectly with the corner of a square (shown in blue). This angle is a right angle, because it is exactly 90^{\circ} .
These angles are NOT right angles, because they are less than 90^{\circ} .
This right triangle (or right-angled triangle) has 1 right angle.
Example 4: identify right angles in a given shape
This irregular polygon is composed of a rectangle and a right triangle. How many interior right angles does it have?
Recall the definition of a right angle.
A right angle is an angle that is exactly 90^{\circ} .
Explain whether or not the angle is right.
A right angle aligns perfectly with the corner of a square (shown in blue). Even though the original shape is not marked with the square, since rectangles and right triangles have right angles, you know these angles are exactly 90^{\circ} .
These angles are NOT right angles, because they are less than 90^{\circ} .
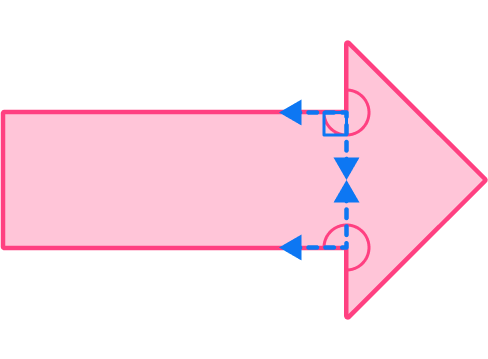
These angles are NOT right angles, because they are more than 90^{\circ} .
This irregular polygon has 3 right angles.
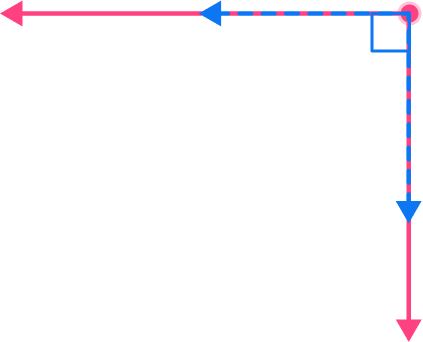
Example 5: identify right angles in intersecting lines
How many right angles are formed by these intersecting lines?
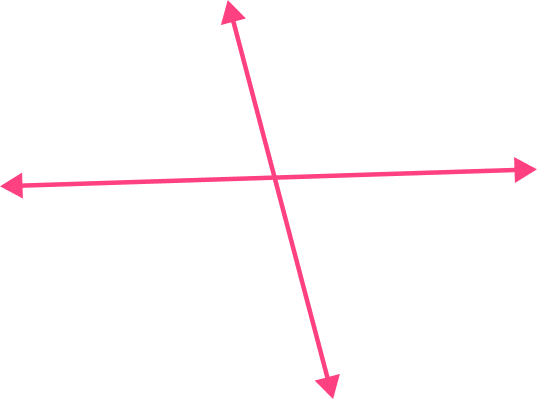
Recall the definition of a right angle.
A right angle is an angle that is exactly 90^{\circ} .
Explain whether or not the angle is right.
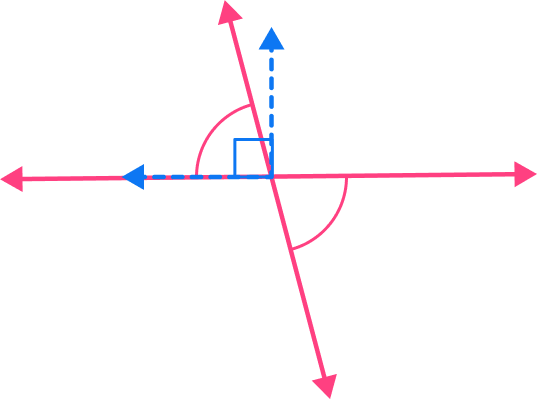
There are four angles formed by the intersecting lines. Two angles are less than 90^{\circ} .
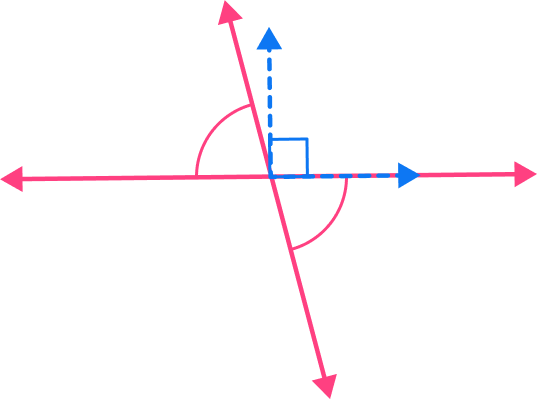
Two angles are greater than 90^{\circ} .
There are no right angles formed by these intersecting lines.
Example 6: identify real-life examples of right angles
How many right angles do you see in the word ‘SMILE’?
Recall the definition of a right angle.
A right angle is an angle that is exactly 90^{\circ} .
Explain whether or not the angle is right.
There are 5 right angles formed by parts in the letters L and E . They are exactly 90^{\circ} .
Teaching tips for a right angle
- Worksheets can provide necessary practice, but since there are so many examples of right angles in real-life, it is important to incorporate these types of activities as well. This could be having students keep a log of examples of right angles they see in the real world or having them move around the classroom with a protractor, finding and recording right angles.
- Encourage students to always prove that a right angle is truly 90 -degrees. Teach them to look for the square mark or the words ‘perpendicular’ in a description. This may also be requiring them to justify their classification with a protractor or a benchmark 90^{\circ} angle (like the edge of a piece of paper).
While students will learn to spot \, 90^{\circ} without these things, it is important that they learn to justify their conclusion as angles like 89^{\circ} and \, 91^{\circ} are close to a right angle, but not classified as such.
Easy mistakes to make
- Confusing right angles with other types of angles
There are other angles besides right: acute angles are between 0^{\circ} and \, 90^{\circ} , obtuse angles are between 90^{\circ} and 180^{\circ} , straight angles are exactly 180^{\circ} , and reflex angles are between 180^{\circ} and 360^{\circ} . Without repeated exposure or practice, it is easy to get these confused.
- Not recognizing a right angle that has an uncommon orientation
Right angles can be in any orientation.
For example,
All the angles below are right, no matter how they are turned.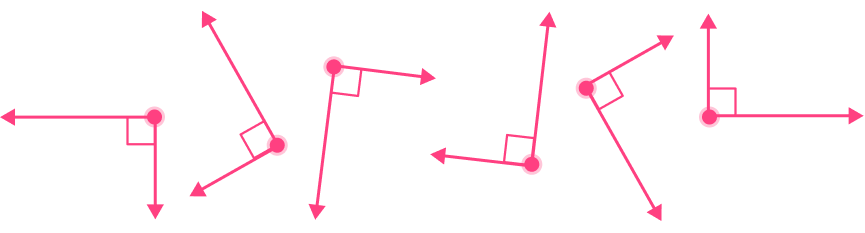
- Not paying attention to the angle in question
Since multiple angles are formed when rays, line segments and straight lines meet, always pay attention to the angle in question.
For example,
If a question is asked about this angle, it is referring to the reflex angle that is marked, not the smaller angle that appears to be right.
Right angle practice questions
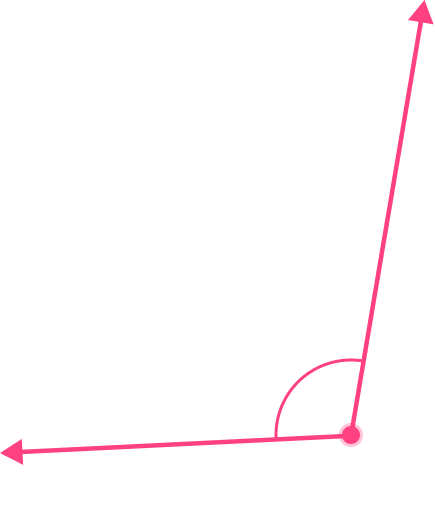
1) Is the angle right? Why or why not?
Yes, because it is exactly 90^{\circ}
No, because it is exactly 90^{\circ}
Yes, because it is greater than 90^{\circ}
No, because it is less than 90^{\circ}
A right angle aligns perfectly with the corner of a square (shown in blue). This angle is a right angle, because it is exactly 90^{\circ} .
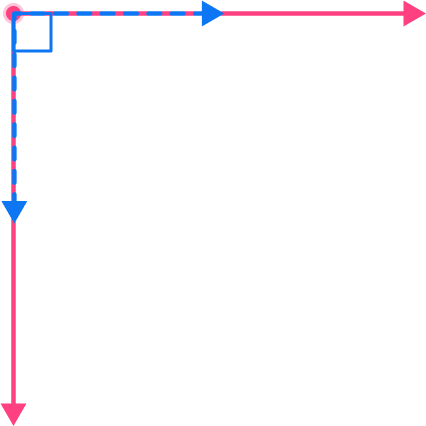
2) Is the angle right? Why or why not?
Yes, because it is exactly 90^{\circ}
No, because it is exactly 90^{\circ}
Yes, because it is greater than 90^{\circ}
No, because it is greater than 90^{\circ}
A right angle aligns perfectly with the corner of a square (shown in blue). This angle is a NOT right angle, because it is greater than 90^{\circ} .
3) How many right angles does a square have?
A square is a four sided shape, where all sides are equal and every angle measures 90^{\circ} . There are four 90^{\circ} angles in every square.
4) Which shape appears to have exactly 2 right angles?
A right angle aligns perfectly with the corner of a square (shown in blue). These 2 angles are right angles, because they are exactly 90^{\circ} .
5) The two lines are perpendicular. Which angle is NOT a right angle?
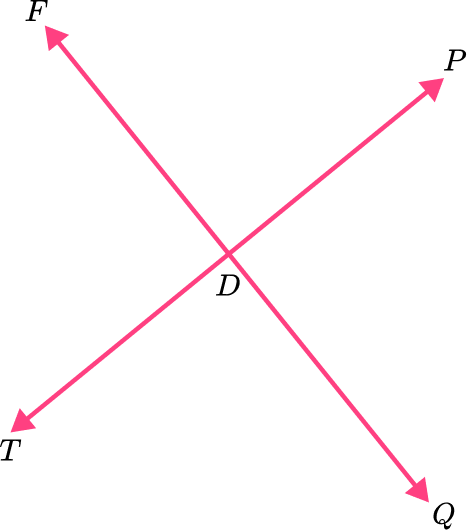
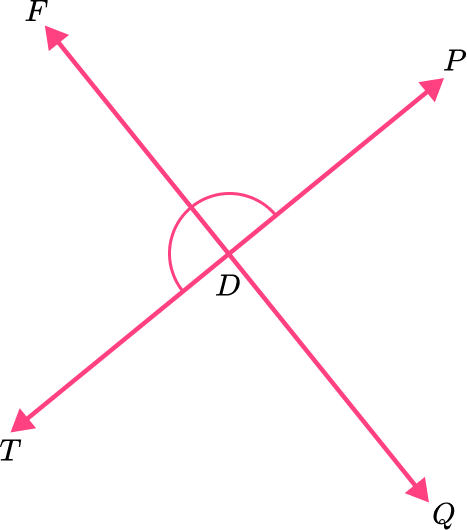
This angle (\angle \mathrm{TDP}\,) is a straight angle and measures 180^{\circ} . It is NOT a right angle.
6) How many right angles does the word ‘FOOT’ have?
There are 5 right angles formed by parts in the letters F and \, T . They are exactly 90^{\circ} .
Right angle FAQs
A triangle can only have one right angle and is always classified as a right triangle. When classifying by sides, isosceles and scalene triangles can also have a right angle. Because all the angles of an equilateral triangle are 60^{\circ} , it will never have a right angle.
The hypotenuse is the longest side on a right triangle.
Angles can be measured in degrees and radians.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!