[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
2D Shapes Lines of symmetry Types of angles Regular polygonsEquilateral triangle
Here you will learn about equilateral triangles, including what an equilateral triangle is and the properties of equilateral triangles.
Students first learn about triangles in kindergarten and 1st grade in geometry with their work in reason with shapes and their attributes. They expand their knowledge of triangles as they progress through elementary school and into secondary school.
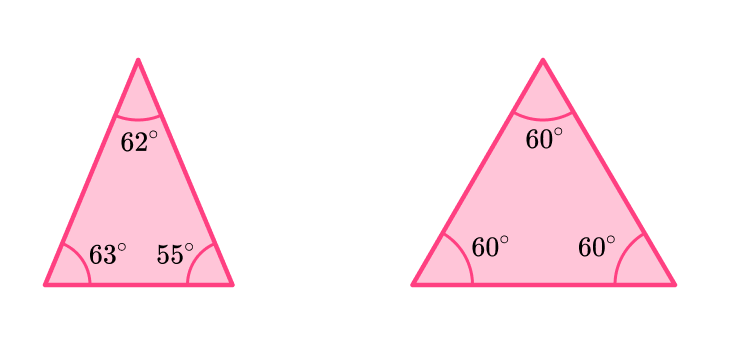
What is an equilateral triangle?
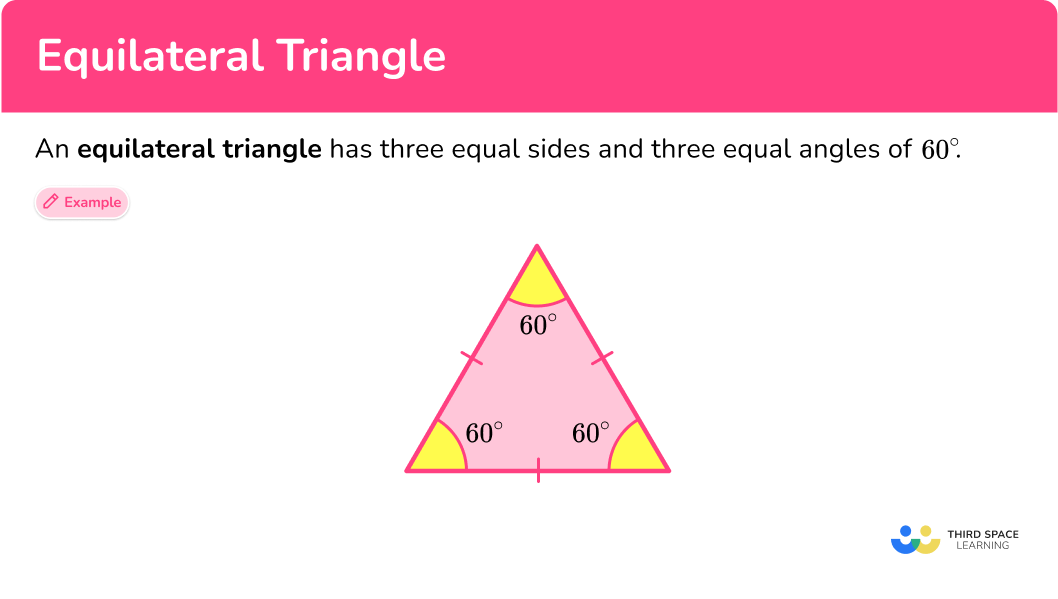
An equilateral triangle has three equal sides and three equal angles.
An equilateral triangle is the simplest of regular polygons because it has the fewest number of sides. Equilateral triangles can also be called equiangular triangles.
Properties of an equilateral triangle:
- All sides are equal length.
- All angles are equal in measure, 60^{\circ}.
The dashes on the sides and the angles of the triangle mean they are equal in measure or congruent.
An equilateral triangle is a special case of an acute triangle, because all the angles are acute and equal.
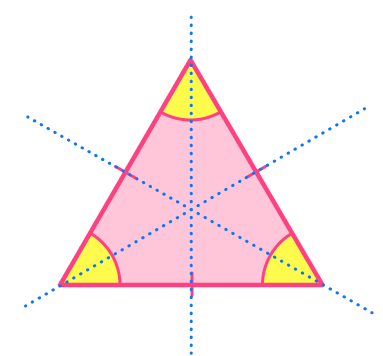
Symmetry of equilateral triangles
An equilateral triangle has three lines of symmetry.
The lines go from one vertex to the middle of the opposite side.
Since equilateral triangles are also regular polygons, notice that the number of lines of symmetry equals the number of sides the polygon has.
What is an equilateral triangle?
Common Core State Standards
How does this apply to 4th grade and 5th grade math?
- Grade 4 – Geometry (4.G.A.3)
Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry.
- Grade 5 – Geometry (5.G.B.3)
Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category.
How to identify an equilateral triangle
In order to classify triangles as equilateral triangles:
- Recall the definition.
- Explain why the triangle fits or does not fit the definition.
![[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
[FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)
Use this quiz to check your grade 4 to 5 students’ understanding of triangles. 10+ questions with answers covering a range of 4th and 5th grade triangle topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] Triangles Check for Understanding Quiz (Grade 4 to 5)
Use this quiz to check your grade 4 to 5 students’ understanding of triangles. 10+ questions with answers covering a range of 4th and 5th grade triangle topics to identify areas of strength and support!
DOWNLOAD FREEEquilateral triangle examples
Example 1: classify triangles
Is this triangle an equilateral triangle?
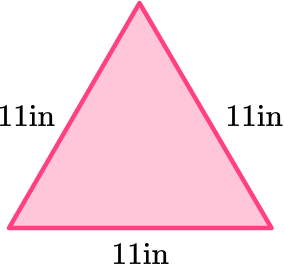
- Recall the definition.
An equilateral triangle has three equal (congruent) sides and three (congruent) equal angles.
2Explain why the triangle fits or does not fit the definition.
This triangle has sides measuring 11 inches. Since the triangle has three equal sides all measuring 11 inches, it is an equilateral triangle.
Example 2: classify triangles
Is triangle ABC an equilateral triangle?
Recall the definition.
An equilateral triangle has three equal (congruent) sides and three (congruent) equal angles.
Explain why the triangle fits or does not fit the definition.
Triangle ABC has two equal (congruent sides). You cannot assume the third side of the triangle is congruent to the other two sides. Also, it does not look to be equal. So, this is NOT an equilateral triangle. This triangle is an isosceles triangle.
Example 3: classifying triangles
Are isosceles triangles also considered equilateral triangles?
Recall the definition.
Equilateral triangles have three equal (congruent) sides and angles.
Isosceles triangles have two equal (congruent) sides and angles.
Explain why the triangle fits or does not fit the definition.
No, isosceles triangles are not also considered equilateral triangles because they only have two equal (congruent) sides and angles.
Example 4: classifying triangles
Are equilateral triangles also considered isosceles triangles?
Recall the definition.
Equilateral triangles have three equal (congruent) sides and angles.
Isosceles triangles have two equal (congruent) sides and angles.
Explain why the triangle fits or does not fit the definition.
Since equilateral triangles have three equal (congruent) sides and angles and isosceles triangles have two equal (congruent) sides and angles, equilateral triangles can be considered isosceles.
Example 5: classifying triangles
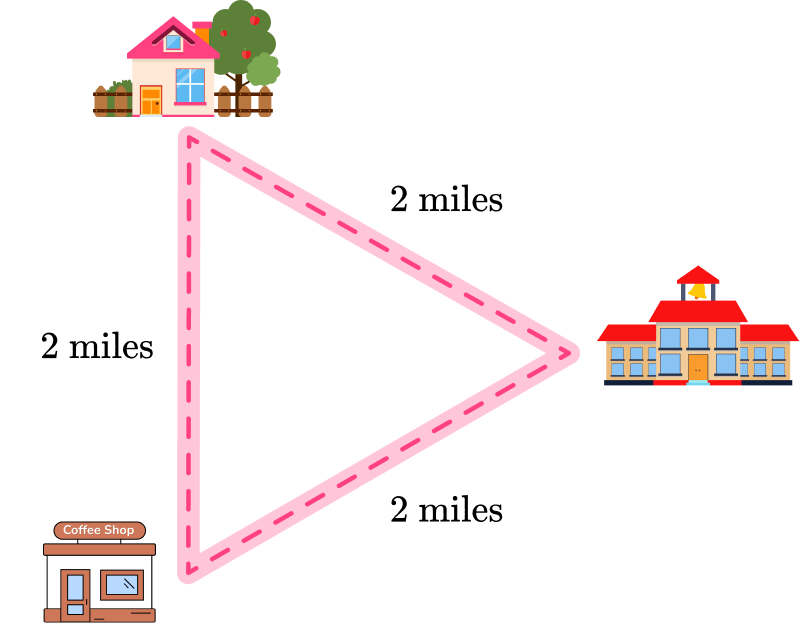
Every day, Teresa walks to school, and after school, she walks to her job at the local coffee shop and then walks home. Below is the path she takes. Does her path form an equilateral triangle?
Recall the definition.
Equilateral triangles have three equal (congruent) sides and angles.
Explain why the triangle fits or does not fit the definition.
The path that Teresa takes every day does form an equilateral triangle because there are 2 miles between each of the locations.
The path between each of the locations makes up the sides of the triangle. Since they are all equal, the path is an equilateral triangle.
Example 6: classifying triangles
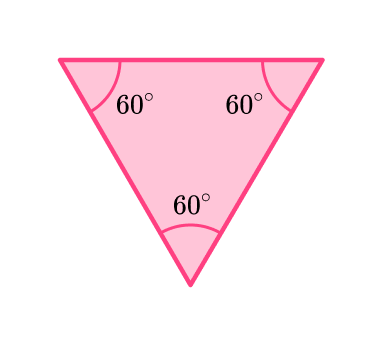
Skye drew the triangle below. What kind of triangle did Skye draw?
Recall the definition.
Equilateral triangles have three equal (congruent) sides and angles.
Explain why the triangle fits or does not fit the definition.
The triangle Skye drew has angles that are each 60^{\circ}. Since each of the angles are equal in measure (congruent), it is an equilateral triangle.
Teaching tips for equilateral triangles
- Incorporate drawing activities where students can use rulers and protractors to create equilateral triangles.
- Incorporate origami activities that are creative and help students understand the properties of triangles, specifically equilateral triangles.
- Although worksheets have their place for practicing skills, using digital platforms for game playing is fun for students and helps them to practice skills. Check out free platforms such as desmos, quizlet, blooket, and quizziz.
Easy mistakes to make
- Thinking that isosceles triangles can be classified as equilateral triangles
Isosceles triangles only have two equal (congruent) sides and angles. Equilateral triangles have three equal (congruent) sides and angles. So, equilateral triangles can be classified as isosceles triangles but isosceles triangles cannot be classified as equilateral triangles.
- Confusing angle facts
Make sure you know your angle facts.- Acute angles are greater than 0^{\circ} and less than 90^{\circ}.
- Right angles equal 90^{\circ}.
- Obtuse angles are greater than 90^{\circ} and less than 180^{\circ}.
Related triangle lessons
- Hypotenuse
- Right triangles
- Acute triangles (coming soon)
- Types of triangles
- Isosceles triangles
- Scalene triangles
Practice equilateral triangle questions
1. Which of these pictures shows an equilateral triangle?
The marks on the sides of the triangle show which lengths are equal.
This triangle was the only one that had all three angles and all three sides marked as being equal.
2. How many lines of symmetry does an equilateral triangle have?
Equilateral triangles have three lines of symmetry.
An equilateral triangle is also a regular polygon, so the number of lines of symmetry is equal to the number of sides.
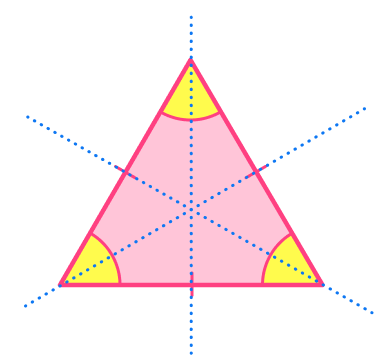
3. Which of the following triangles is NOT an equilateral triangle?
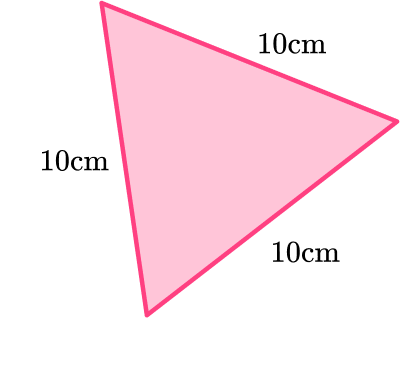
An equilateral triangle has three equal sides and three equal angles.
This triangle has two equal sides and one 90^{\circ} angle.
So, it is not an equilateral triangle. It is an isosceles right triangle.
4. Which picture below represents an equilateral triangle?
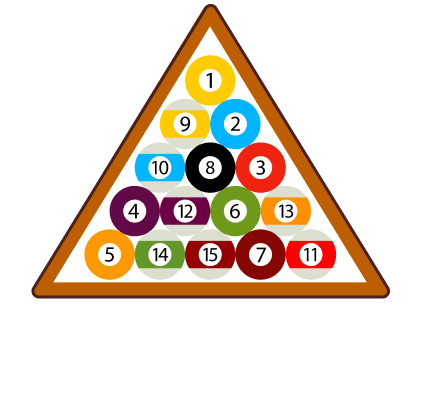
The picture of the pool rack is the only image that appears to be an equilateral triangle.
It looks to have three equal (congruent) sides and angles.
5. The angle measures of a triangle are 60^{\circ}, 60^{\circ}, and 60^{\circ}. Which of the following best classifies the triangle?
Obtuse triangle
Isosceles triangle
Equilateral triangle
Right isosceles triangle
Equilateral triangles have three equal (congruent) sides and angles.
Each angle of an equilateral triangle is 60^{\circ}.
So, the best classification of a triangle with each angle being 60^{\circ} is an equilateral triangle.
6. An equilateral triangle will have ______ right angles.
Equilateral triangles have no right angles. Each angle of an equilateral triangle is equal in measure, which is 60^{\circ}.
Equilateral triangle FAQs
Yes, equilateral triangles have equal interior angles and equal exterior angles.
No, the Pythagorean theorem can only be used on right triangles to find missing side lengths.
No, equilateral triangles do not have a side called the hypotenuse. The hypotenuse is the name of the longest side of a right triangle. So, only right triangles have hypotenuses.
You find the area of an equilateral triangle using the formula for area of a triangle, A=\frac{1}{2} \cdot b \cdot h, where h, represents the height of an equilateral triangle.
You can add up the sides of an equilateral triangle to find the perimeter or take one of the side lengths and multiply it by 3 since they are all the same.
Angle bisectors are special line segments in a triangle that divide each angle in half. In middle and high school, you will learn about all the special segments of triangles (perpendicular bisectors, medians, angle bisectors, and altitudes).
Properties of triangles will be further explored in high school to explore angles in parallel lines, circle theorems, trigonometry and Pythagoras’ theorem.
The altitude of an equilateral triangle is the same thing as the height of an equilateral triangle.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!