What Are Coordinates: Explained For Primary School Parents And Kids

Learning what coordinates are and how they work can be one of the most confusing parts of primary school maths. That’s why we’ve put together this guide to help you explain coordinates easier to your children!

What are coordinates?

Coordinates are two numbers (Cartesian coordinates), or sometimes a letter and a number, that locate a specific point on a grid, known as a coordinate plane. A coordinate plane has four quadrants and two axes: the x axis (horizontal) and y axis (vertical). (One way of helping children to remember which of these is which is to tell them that the x axis goes across because ‘x’ is a cross.)

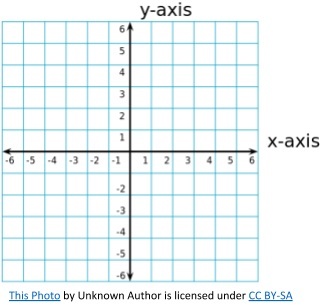
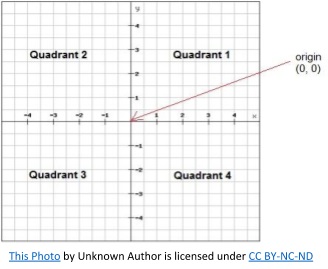
Children are introduced to coordinates in the first quadrant (the top right quadrant) as both coordinate digits will be positive. The point at which the two axes intersect is called the origin – the coordinates of this point are (0, 0). 

Coordinates are written as (x, y) meaning the point on the x axis is written first, followed by the point on the y axis.

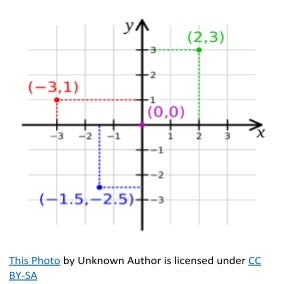
Some children may be taught to remember this with the phrase ‘along the corridor, up the stairs’, meaning that they should follow the x axis first and then the y.

When will my child learn about coordinates in primary school?

Coordinates are first taught in Year 4, where children describe positions on a 2-D grid as coordinates in the first quadrant and plot specified points and draw sides to complete a given polygon.

In the National Curriculum guidance, coordinates are referenced multiple times throughout the rest of KS2:

• Year 4: Pupils draw a pair of axes in one quadrant, with equal scales and integer labels. They read, write and use pairs of coordinates, for example (2, 5), including using coordinate plotting ICT tools.
• Year 5: Pupils recognise and use reflection and translation in a variety of diagrams, including continuing to use a 2-D grid and coordinates in the first quadrant. Reflection should be in lines that are parallel to the axes.
• Year 6: Pupils draw and label a pair of axes in all four quadrants with equal scaling. This extends their knowledge of one quadrant to all four quadrants, including the use of negative numbers. Pupils draw and label rectangles (including squares), parallelograms and rhombuses, specified by coordinates in the four quadrants, predicting missing coordinates using the properties of shapes. These might be expressed algebraically for example, translating vertex (a, b) to (a – 2, b + 3); (a, b) and (a + d, b + d) being opposite vertices of a square of side d.

The teaching of coordinates ends in Year 6, where children learn to describe positions on the full coordinate grid (all four quadrants) and draw and translate simple shapes on the coordinate plane, and reflect them in the axes.

How do coordinates relate to other areas of maths?

Coordinates sometimes appear in other areas of maths in upper KS2, specifically graphs and algebra. In Year 5 and 6 respectively, the non-statutory guidance advises that pupils connect their work on coordinates and scales to their interpretation of time graphs and that pupils should be introduced to the use of symbols and letters to represent variables and unknowns in mathematical situations that they already understand, such as… coordinates.

Wondering about how to explain other key maths vocabulary to your children? Check out our Primary Maths Dictionary, or try these other terms related to co-ordinates:

• What Is The Perimeter
• What Is BODMAS (and BIDMAS)?
• Properties of shapes
• What are 2D shapes?
• What are 3D shapes?

Practice questions

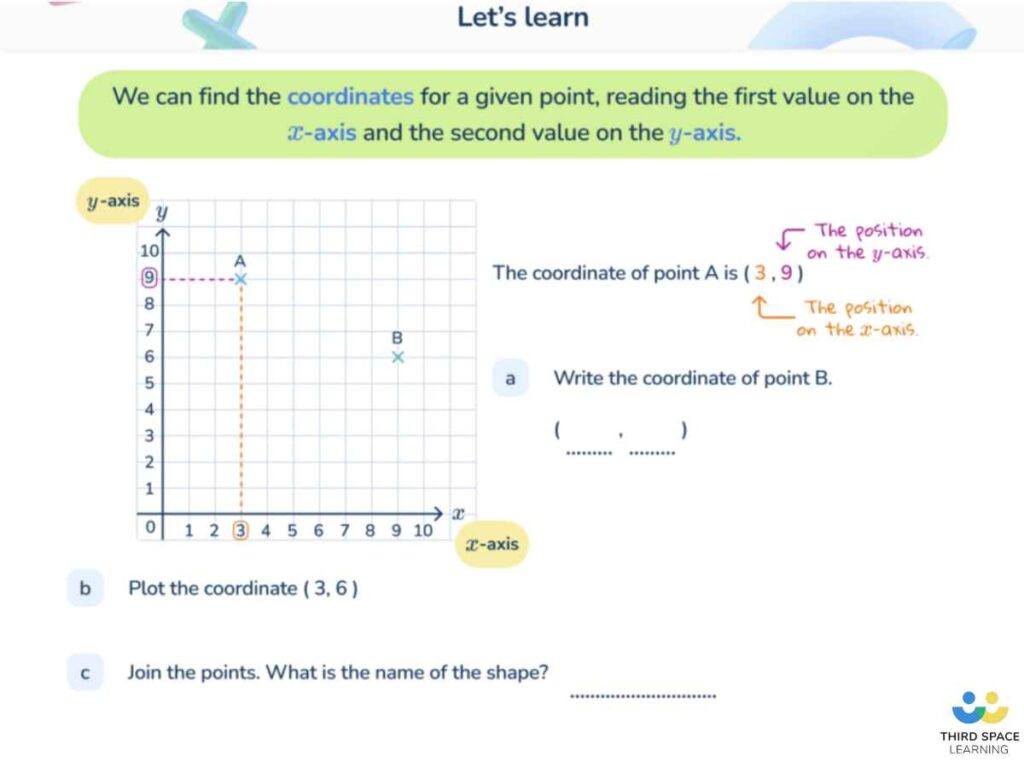
1. Layla draws a square on this coordinate grid. Three of the vertices are marked. What are the coordinates of the missing vertex?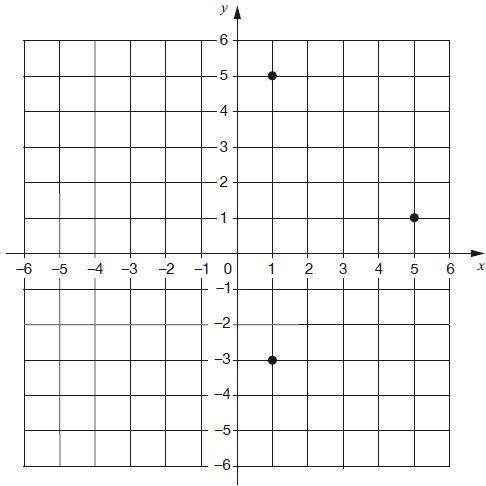

(Answer: -3, 1)

2. In this diagram, R is an equal distance from P and Q. What are the coordinates of R?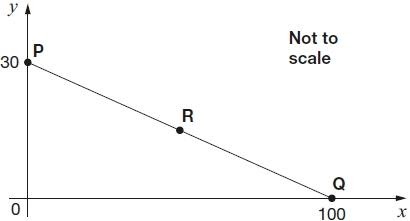

(Answer: 50, 15)

3. This diagram shows two identical rectangles on coordinate axes. Write the coordinates of point A and point B.

(Answer: A = 12, 6 & B = 19, 3)

4. Here is a kite. Write the coordinates of point D.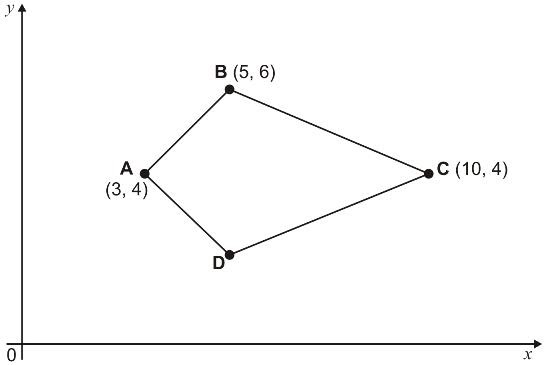

(Answer: D = 5, 2)

5. A counter is placed on square D4. It is moved 2 squares right and 3 squares down. Write the position of the square it lands on.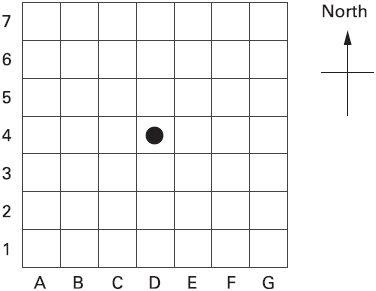

(Answer: F1)