What Are Vertices, Faces And Edges? Explained For Primary School
Find out what vertices, faces and edges mean, and how to work out the number of vertices, faces and edges for any shape. There are also examples of the number of edges, faces and vertices of the most common shapes.
Vertices, faces and edges are introduced in the national curriculum in Year 2, and so the following information can be used with pupils throughout primary school years. Even Year 1 pupils can begin to engage with properties of shapes in this way if you want to give them a head start!
What are vertices in shapes?
Vertices in shapes are the points where two or more line segments or edges meet (like a corner). The singular of vertices is vertex. For example a cube has 8 vertices and a cone has one vertex.
Vertices are sometimes called corners but when dealing with 2D and 3D shapes, the word vertices is preferred.
A cube has 8 vertices. 7 are visible here and one is hidden.
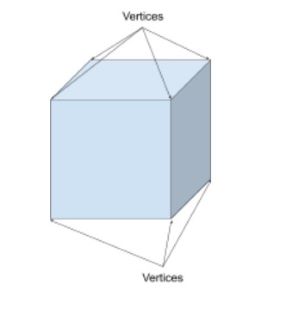
What are edges?
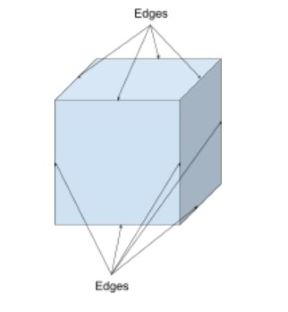
Edges are the lines of a 2D or 3D shape. They are the lines that join the vertices (corner points) up to form shapes and faces.
Although many shapes have straight lines and straight edges, there are shapes which have curved edges, such as a hemisphere. A cube will have 12 straight edges as seen below; 9 are visible and 3 are hidden.
FREE 3D Shapes Independent Recap Worksheets
Help your Year 2 (and older) pupils revise vertices, faces and edges with our free Independent Recap worksheets.
FREE 3D Shapes Independent Recap Worksheets
Help your Year 2 (and older) pupils revise vertices, faces and edges with our free Independent Recap worksheets.
Download Free Now!What are faces?
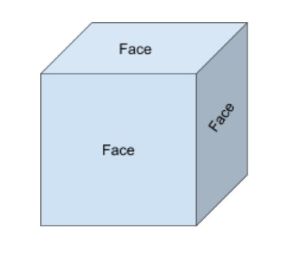
Faces are the flat surface of a solid shape. For example, a cuboid has 6 faces. When thinking about 2d and 3d shapes, it is important to know that a 2d shape merely represents the face of a 3d shape.
It is also important to know that as our reality is constructed in 3 dimensions, it is impossible to physically handle 2d shapes as we are surrounded by 3-dimensional shapes. Therefore, if in your classroom there is a drawer labelled ‘2d Shapes’ this should be removed as it is teaching children a misconception. Although an interactive concept for the classroom, 2d shapes can only exist as 2 dimensional drawings.
You can have both flat faces and curved faces, but I find it helpful to refer to curved faces as curved surfaces as it matches well with the visual of the shape.
There are three faces that are visible and three that are hidden on the cube below.
Vertices, faces and edges of common 3d shapes
How many faces, edges and vertices does a cuboid have?
A cuboid has 8 vertices.
A cuboid has 12 edges.
A cuboid has 6 faces.

How many faces, edges and vertices does a cylinder have?
A cylinder has 0 vertices.
A cylinder has 2 edges.
A cylinder has 2 faces and 1 curved surface.

How many faces, edges and vertices does a hemisphere have?
A hemisphere has 0 vertices.
A hemisphere has 1 curved edge.
A hemisphere has 1 face and 1 curved surface.

How many faces, edges and vertices does a cone have?
A cone has 1 vertex.
A cone has 1 edge.
A cone has 1 face and 1 curved surface.

How many faces, edges and vertices does a tetrahedron have?
A tetrahedron has 4 vertices.
A tetrahedron has 6 edges.
A tetrahedron has 4 faces.

How many faces, edges and vertices does a sphere have?
A sphere has 0 vertices.
A sphere has 0 edges.
A sphere has 1 curved surface.

How many faces, edges and vertices does a prism have?
A prism is a solid object, geometric shape, or polyhedron where the faces of both ends are the same shape.
Students will come across many types of prisms throughout their schooling, including rectangular prisms, cubes, cuboids, triangular prisms, pentagonal, and hexagonal prisms. Here are some examples of different prisms along with the number of faces, edges, and vertices they have.

When do children learn about vertices, faces and edges in primary school?
Children need to be formally introduced to the vocabulary of vertices, faces and edges in Year 2 when studying geometry. However, teachers may make the choice to introduce this vocabulary earlier on.
Year 2 pupils should be able to:
- identify and describe the properties of 3-D shapes, including the number of edges, vertices and faces
The non-statutory guidance states that:
- Pupils handle and name a wide variety of common 2-d and 3-d shapes including: quadrilaterals and polygons, and cuboids, prisms and cones, and identify the properties of each shape (for example, number of sides, number of faces). Pupils identify, compare and sort shapes on the basis of their properties and use vocabulary precisely, such as sides, edges, vertices and faces.
From this point on, the national curriculum does not reference vertices, faces and edges explicitly again, so teachers in other year groups will have to continue to use this vocabulary when looking at shape
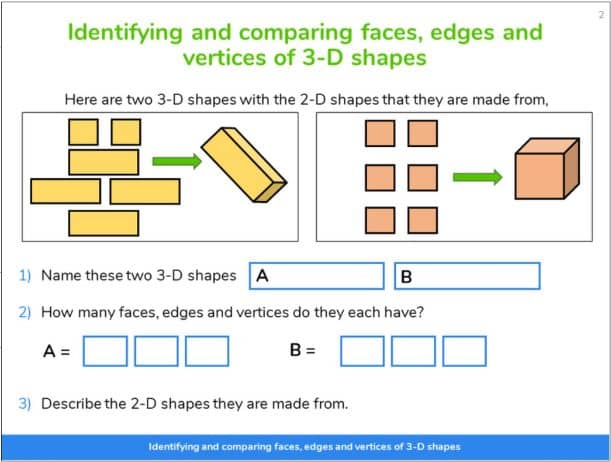
How do vertices, faces and edges relate to other areas of maths?
Students will use vertices, faces and edges when looking at different shapes in other areas of the maths curriculum. It is an important foundation for later years when dealing with different maths theorems, such as graph theory and parabolas.
For example, knowing what edges are and identifying them on compound shapes is important in finding the perimeter and area of 2d compound shapes.
How do vertices, faces and edges relate to real life?
Any object in real life has vertices, faces and edges. For example, a crystal is an octahedron – it has eight faces, twelve edges and six vertices (a 3D shape octagon). Knowing these properties for different three-dimensional shapes lays the foundation for various industries such as architecture, interior design, engineering and more.
Vertices, faces and edges example questions
1. Explain what a vertex is.
(Answer: A vertex is where two lines meet)
2. How many edges does a triangular prism have?
(Answer: 9)
3. How many vertices does a cone have?
(Answer: 1 vertex)
4. How many faces does a cuboid have? What are the 2D shapes of those faces?
(Answer: 6 faces. They can have 2 square faces and 4 rectangular faces or just 6 rectangular faces.)
5. For all the common prisms (cubes, cuboids, triangular prisms, pentagonal prisms and hexagonal prisms) add the faces and vertices together and subtract the edges. What do you notice about the answers?
(Answer: The answer is always 2. This is known as Euler’s formula (number of vertices – number of edges + number of faces = 2)
Wondering about how to explain other key maths vocabulary to your children? Check out our Primary Maths Dictionary, or try these:
You can find plenty of geometry lesson plans and printable worksheets for primary school pupils on the Third Space Learning Maths Hub.
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.





