What Is Long Division? Explained For Primary School
Long division is introduced in Year 6. It is important that children understand the concept of division before this method is taught as this formal method is quite an abstract process. The long division method is usually used to divide by larger numbers than the short division method.
- What is long division?
- Long division method: How to do long division
- How to explain long division
- When do children learn about long division in school?
- How does long division relate to other areas of maths?
- How does long division link to real life?
- Long division worked examples
- Practise long division problems
- Long division FAQs
3 Long Division Worksheets for Year 3-6 Classes
Download this free set of long division worksheets for Years 3-6 to help your students practice their long division skills!
Download Free Now!What is long division?
Long division is a formal method of division often called the bus stop method. See the examples below from the Mathematics Appendix 1 in the national curriculum.
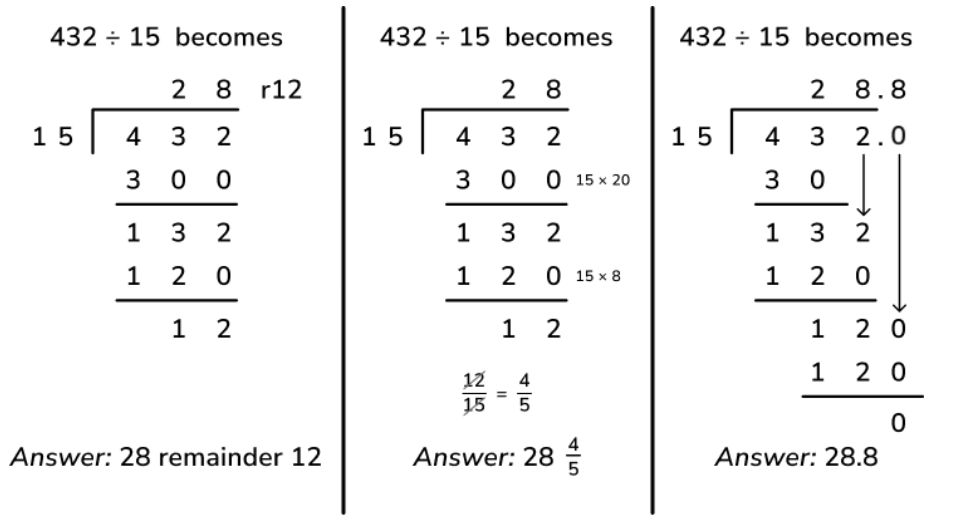
It is different from the short division method in that the long division written method is less compact. The long method of division is most often used when dividing by large numbers – in the primary curriculum, this is usually a 2-digit number (or three digits as a challenge). It can be used with or without remainders. The first two examples above are more commonly known as ‘chunking’; the third example is an expanded version of the short division method.
See also: What is division
Long division method: How to do long division
Long division is laid out in the same way as short division: dividend (the number being divided) under the ‘bus stop’, divisor (number the dividend is being divided by) to the left of the ‘bus stop’; quotient (answer) on top, with each place value aligned with the dividend.
Chunking
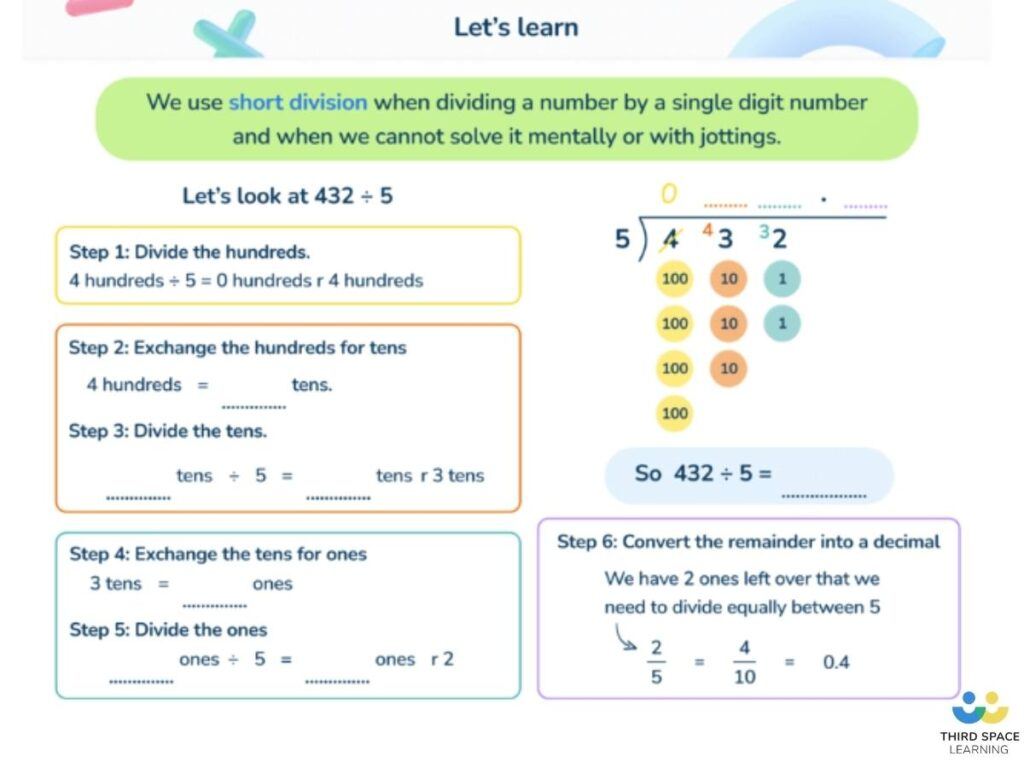
The example below uses the ‘chunking’ form of long division to calculate 432 ÷ 15. This variation of the method involves ‘chunking’ a section of the dividend a bit at a time – firstly by subtracting 20 lots of the divisor, which leaves 132, then by subtracting another 8 lots of the divisor, which leaves 12. As this amount is smaller than the divisor, this is the remainder. The quotient is 28, so the final answer is 28r12 (or, if represented as a fraction, 28 and 12/15 or 28 and ⅘ when simplified).
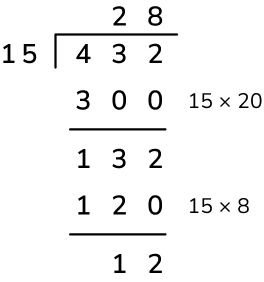
Long division steps
There are five long division steps that can be used to simplify this version of the method:
- Divide
- Multiply
- Subtract
- Bring the next number down
- Repeat
See how the steps are applied using this example:
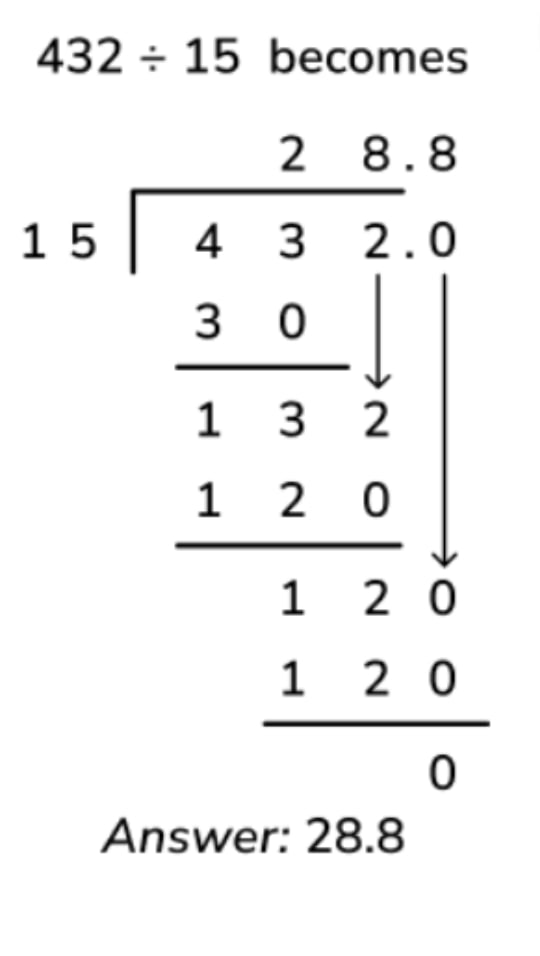
1.Divide: Starting with the first digit of the dividend, divide 4 hundreds by 15. We cannot do this, so a 0 could be placed above the 4 here, but instead we can just see the 4 hundreds as 40 tens alongside the 3 tens (the next digit of the dividend). Now divide 43 tens by 15, which is 2 tens. This digit is placed above the 3 tens and becomes the first digit of the quotient.
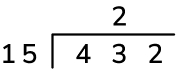
2. Multiply: We need to calculate the remainder for this first step of the division – to do this, firstly multiply the first digit of the quotient, 2 tens, by the divisor, 15, to get 30 tens. Place this underneath the dividend, making sure to align the place values correctly.
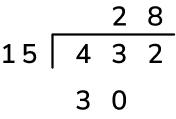
3. Subtract: To finish calculating the remainder for this first step of the division, finally subtract 30 tens from 43 tens to get 13 tens.
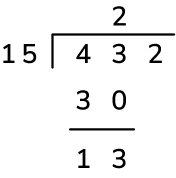
4. Bring the next digit down: In short division, we would place the remainder from each step before the next digit in the dividend – in this case, the 13 would be written to the top left of the digit ‘2’ to read 132. In long division, we just bring the next digit of the quotient down – this achieves the same thing but is just a bit easier to read!
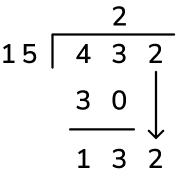
5. Repeat: Now we start the division process again from…
– Step 1: divide (divide 132 ones by 15 and place the answer, 8 ones, in the quotient); – Step 2: multiply (multiply the next digit of the quotient, 8 ones, by the divisor, 15, and place the answer, 120 ones, underneath 132 ones);
– Step 3: subtract (finish calculating the remainder to this next step by subtracting 120 ones from 132 ones to get 12 ones);
– Step 4: bring the next digit down (as the quotient won’t be a whole number, we will need to add a decimal point and a zero to calculate the remainder as a decimal, so the zero gets brought down to make 120 tenths);
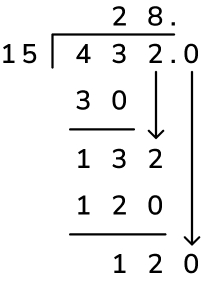
– Step 5: repeat (divide 120 tenths by 15 to get 8 tenths and place this in the quotient as the first – and only – decimal place; multiply 8 tenths by 15 to get 120 tenths; subtract this from 120 tenths to calculate the remainder, which is 0; there is now no next digit to bring down so, as the remainder is now 0, the calculation is complete).
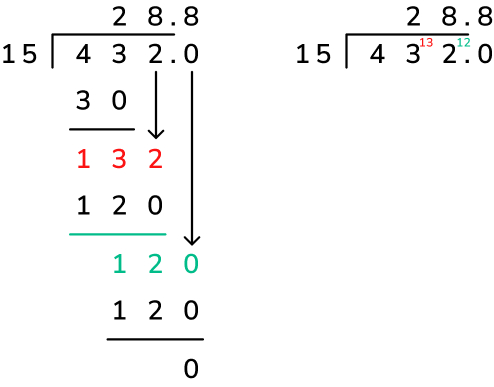
As you can see from the example below, short division can also be used to solve this calculation – both methods give the correct answer but the ‘long’ method is just the expanded version of the ‘short’ method. Rather than doing some of the calculations mentally in the short division method to calculate the remainder for each step (to work out the remainder of the first step as 13 tens, or 130 ones, and the second step as 12 ones, or 120 tenths), long division lays these same calculations out as part of the method itself.
How to explain long division
If children struggle with multiplication and division, particularly times tables, it helps to list multiples of the divisor before completing the division to reduce the cognitive demand on the child when working through the method. This can be done with short division too, but let’s use the example above to show how listing the multiples would help.
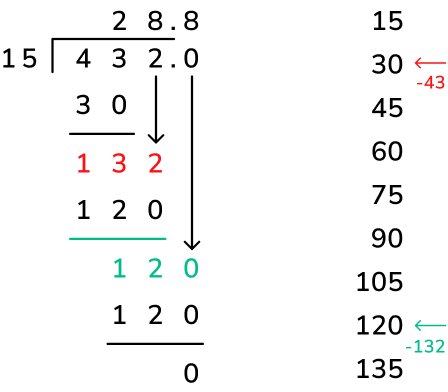
Firstly, list 9 multiples of the divisor: this can be done by repeated addition (15 + 15 = 30, + 15 = 45, + 15 = 60, etc.) or partitioning (15 can be partitioned into 10 and 5; list the multiples of 10 – 10, 20, 30 etc. – and the multiples of 5 – 5, 10, 15 etc. – and then add them together to create each multiple – 10 + 5 = 15, 20 + 10 = 30, 30 + 15 = 45 etc.).
When completing step 1 of the long division method (the expanded version of short division), the multiples make it a lot easier. Firstly, in the example above, use the multiples to calculate 43 tens divided by 15 – we can see that 43 ‘fits’ above 30, which is 2 multiples of 15. We can continue the division process until we get to the ‘repeat’ step and calculate 132 ones divided by 15 – we can see that 132 ‘fits’ above 120, which is 8 multiples of 15.
To ease the children into this version of the long division method, try it first with a one digit divisor. They will no doubt be used to applying the short division method when dividing by one-digit, but comparing both (as in the example below) is a clear sequential step between the short and long method.
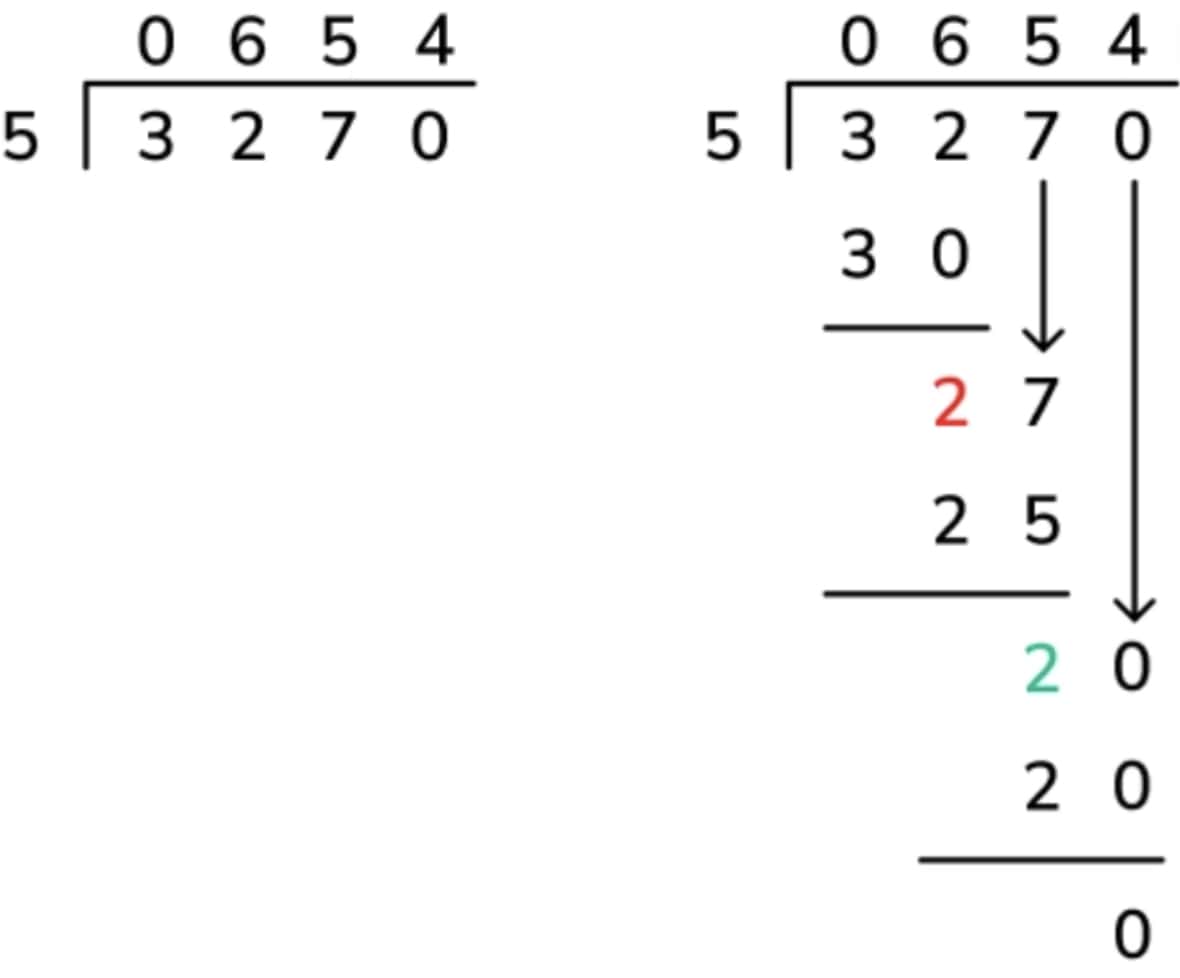
Read for more detail about the long division method in Year 6.
When do children learn about long division in school?
Long division isn’t taught until the final year of primary school. The National Curriculum states that Year 6 pupils should be taught to divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context.
How does long division relate to other areas of maths?
Long division may be required in multi-step problems (word problems requiring more than one mathematical operation to solve it, e.g. addition and multiplication), but as the cognitive demand of a maths problem like this is already quite high, it’s more likely that a short division method would be more appropriate for whatever division may be expected.
How does long division link to real life?
Whenever something needs to be shared equally between a large number of groups and the division cannot be done mentally, long division can be used.
Long division worked examples
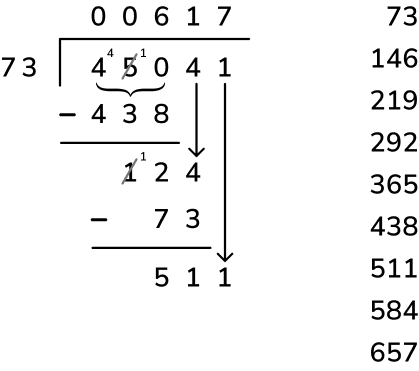
1.45,041 ÷ 73
Answer: 617
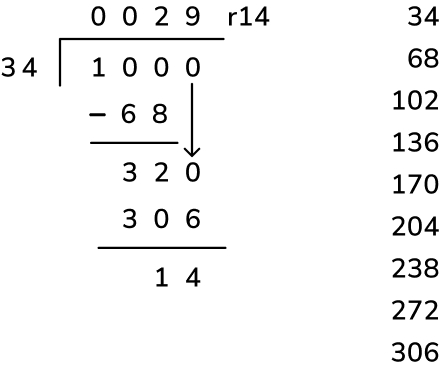
2. Adam is making booklets. Each booklet must have 34 sheets of paper. He has 2 packets of paper. There are 500 sheets of paper in each packet. How many complete booklets can Adam make from 2 packets of paper?
Answer: 2 packets of 500 sheets = 1,000 sheets. 1,000 ÷ 34 = 29 complete booklets
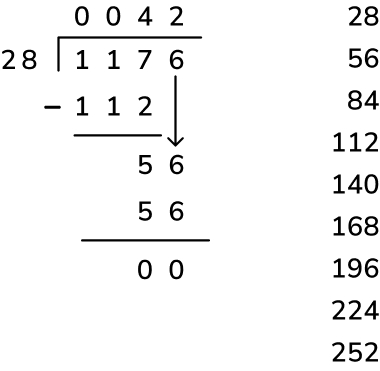
3. A supermarket manager needs to order 1,176 apples. Apples are sold in trays containing 28 apples. How many trays of apples does the manager need to order?
Answer: 1,176 ÷ 28 = 42 trays
Practise long division problems
- 1,632 ÷ 24. Answer: 68
- 42,028 ÷ 79. Answer: 532
- For a school trip, each coach holds 42 passengers. If there are 521 children and teachers in total, how many coaches does the school need to book? Answer: 13 coaches
- A factory makes 4,923 toy cars which are packed in boxes of 15. How many toy cars are left over? Answer: 3
- 21 people each win an equal share of £9,072. How much does each person win? Answer: £432
Looking for more division and long division resources? Third Space Learning offers a comprehensive library of primary and secondary maths resources. See our blogs on our long division examples and long division questions.
In addition to teaching and learning resources, Third Space Learning also offers one-to-one online tuition to support students. Personalised to the needs of each individual child, our online tutoring courses aim to fill gaps in learning and boost confidence in maths.
Long division FAQs
Divide, multiply, subtract, bring the next digit down and repeat the previous steps.
Long division is the expanded version of short division – each step is exactly the same but we just write it out instead of doing it mentally!
When dividing by larger numbers, It is often more accurate than short division because there is less we have to ‘hold’ in our head – all the calculations are laid out for us.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.