What Is Order Of Operations: Explained For Primary School 

The order of operations is also known as BIDMAS, BODMAS, BEDMAS, PEMDAS or PEDMAS (to name a few!). It isn’t taught until Year 6 at primary school.

What is the order of operations 

The order of operations is the order in which the four mathematical operations (addition, subtraction, multiplication or division) should be completed when there is more than one in a number sentence together. There are a variety of acronyms to help remember the correct order; BIDMAS, BODMAS, BEDMAS and PEMDAS:

BIDMAS	BODMAS	BEDMAS	PEMDAS (also known by the mnemonic ‘please excuse my dear Aunt Sally’)
Brackets	Brackets	Brackets	Parentheses
Indices	Powers Of	Exponents	Exponents
Division	Division	Division	Multiplication
Multiplication	Multiplication	Multiplication	Division
Addition	Addition	Addition	Addition
Subtraction	Subtraction	Subtraction	Subtraction

Brackets and parentheses are the same thing, as are indices, ‘powers of’ and exponents. For the last four terms (‘DMAS’), it is perhaps more useful to think of it as ‘division and multiplication’ than ‘addition and subtraction’. This is because the two operations in each pair are equally weighted – it doesn’t matter which you calculate first as the answer will be the same either way.

For example, let’s take the following expression: 15 – 3 x 2 + 4. As per the order of operations, we’d start with multiplication 3 x 2 = 6. We are therefore left with 15 – 6 + 4. Because addition and subtraction are weighted equally, the remaining operations can be done in any order (as proved below), although it is often easier to calculate the expression from left to right: 15 – 6 is 9 and 9 + 4 = 13.

Multiplication and division can be done in any order

Let’s take the example of 5 x 6 ÷ 3. If we complete the multiplication first (5 x 6), we are left with 30 ÷ 3 = 10. If we complete the division first (6 ÷ 3), we are left with 5 x 2 = 10

Addition and subtraction can be done in any order

This may be a little complex to teach in primary school, depending on children’s understanding of number, hence the recommendation to work from left to right if there is only addition and subtraction left. As each integer in the example above is positive, the mathematical expression is actually (+15) – (+6) + (+4). If we do the subtraction first, we get (+15) – (+6) which is (+9), then +9 + (+4) = (+13). If we do the addition first, we get (-6) + (+4) which is (+2), then (+15) – (+2) = 13. 

Order of operations examples

14 – 2 x 6 + 5 = 7 (as per the order of operations). A common misconception would be to calculate this number sentence from left to right, which would get the incorrect answer of 77.

24 ÷ (3 + 1) = 6.  

Third Space Learning’s online, one-to-one tuition lessons walk students through example questions giving them a step by step breakdown of how to tackle a question before the student tries one themselves. This ‘I do, we do, you do’ approach helps to build student understanding, skills and confidence in maths.

When do children learn about order of operations in the national curriculum 

The National Curriculum doesn’t require schools to teach this until Year 6, where “pupils should be taught to use their knowledge of the order of operations to carry out calculations involving the four operations”. There is also non-statutory guidance recommending that “pupils [in Year 6] explore the order of operations using brackets; for example, 2 + 1 x 3 = 5 and (2 + 1) x 3 = 9.”

How does order of operations relate to other areas of maths

In algebra in Year 6, there is non-statutory guidance that “pupils should be introduced to the use of symbols and letters to represent variables and unknowns in mathematical situations that they already understand”. This is often through word problems such as the example below, taken from the 2022 SATs paper.

This could be represented as t = 15 + 12.5h, where t = total cost and h = number of hours. In algebra, a number and a letter together mean they should be multiplied together – so in the example above, as per the order of operations, the multiplication is completed first (12.5 x number of hours) before then adding 15 to calculate the total cost.

Order of operations in real life

When having to solve multi-step mathematical problems in real life, the order of operations will often be relevant. For example, buying tickets online for £12 each with a £3 charge for online transactions would require the multiplication to be calculated first (£12 x number of tickets) and the addition after (adding £3 to the final amount).

3 worked examples for order of operations 

1. 5² x (9 – 7)
   As per the order of operations, we complete what is inside the brackets first (9 – 7 = 2), then indices (5² = 25), then multiplication (25 x 2), so the correct answer is 50.

2. Write the missing number to complete the calculation: 5 + 2 x 3 – __ = 6

As per the order of operations, complete the multiplication first. 2 x 3 = 6, so we are left with 5 + 6 – __ = 6. Addition/subtraction are next, which leaves 11 – __ = 6, so the missing number is 5. Without using the order operations (so completing the calculation from left to right), you would get the wrong answer of 15 (5 + 2 = 7, then 7 x 3 = 21, leaving 21 – __ = 6).

3. By placing one pair of brackets in this number sentence, how many different answers can you make? 4 + 5 x 2 – 3

• Putting the brackets round the whole number sentence, the first three numbers [(4 + 5 x 2) – 3], the last three numbers [(4 + (5 x 2 – 3)] or the multiplication alone [4 + (5 x 2) – 3] gives the same answer as if there were no brackets at all (the answer being 11).
• (4 + 5) x 2 – 3 = 15 [Completing the brackets first: 4 + 5 = 9; then the multiplication: 9 x 2 = 18; then the subtraction: 18 – 3 = 15]
• 4 + 5 x (2 – 3) = -1 [Completing the brackets first: 2 – 3 = -1; then the multiplication: 5 x -1 = -5; then the addition: 4 + -5 = -1] 

So there are three different answers depending on where the pair of brackets is placed: 11, 15 or -1.

5 order of operations practise questions and answers 

Challenge your students’ problem solving skills with these BODMAS questions.

1) Write the missing numbers to make these calculations correct.

a. 200 x ___ – 200 = 200

b. (100 – ___) x 100 = 100

Answer: a) 2   b) 99

2) 60 – 24 ÷ 6 =

Answer: 56

3) Write the >, < or = in each of the boxes below to make the statements correct.

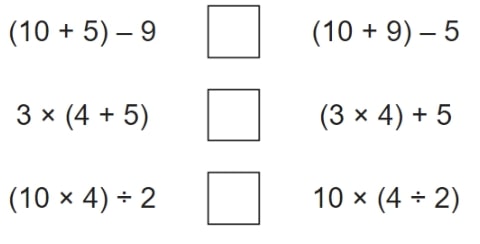
Answer: <, >, =

4) Write what the missing numbers could be: 120 = 100 + (__ – __)

Answer: Any two numbers with a difference of 20, e.g. 40 and 20, or 31 and 11 etc.

5) 900 ÷ (45 × 4) =

Answer: 5

Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.

Since 2013 we’ve helped over 150,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.