BODMAS Questions That Will Test Your Primary School Pupils

BODMAS (also known as BIDMAS) is an acronym to help remember the order of operations (the order in which mathematical operations must be completed). Pupils will first encounter this in the Year 6 syllabus, with predominantly arithmetic questions containing two or three different operations.

What are BODMAS questions?

BODMAS stands for:

1. Brackets (also called parentheses)
2. Powers Of (or Indices in BIDMAS)
3. Division and Multiplication
4. Addition and Subtraction

There is a common misconception that in the BODMAS rule, division precedes multiplication, or that addition precedes subtraction; however, multiplication and division are of equal “importance”, as are addition and subtraction (but less so than multiplication and division). In the rule of BODMAS, these operations are completed from left to right (although addition and subtraction can actually be completed in any order and still achieve the same answer).

NB: The term PEMDAS rule, often used in the United States, is the same, but instead stands for parentheses, exponents, multiplication and division, addition and subtraction.

How to solve BODMAS questions

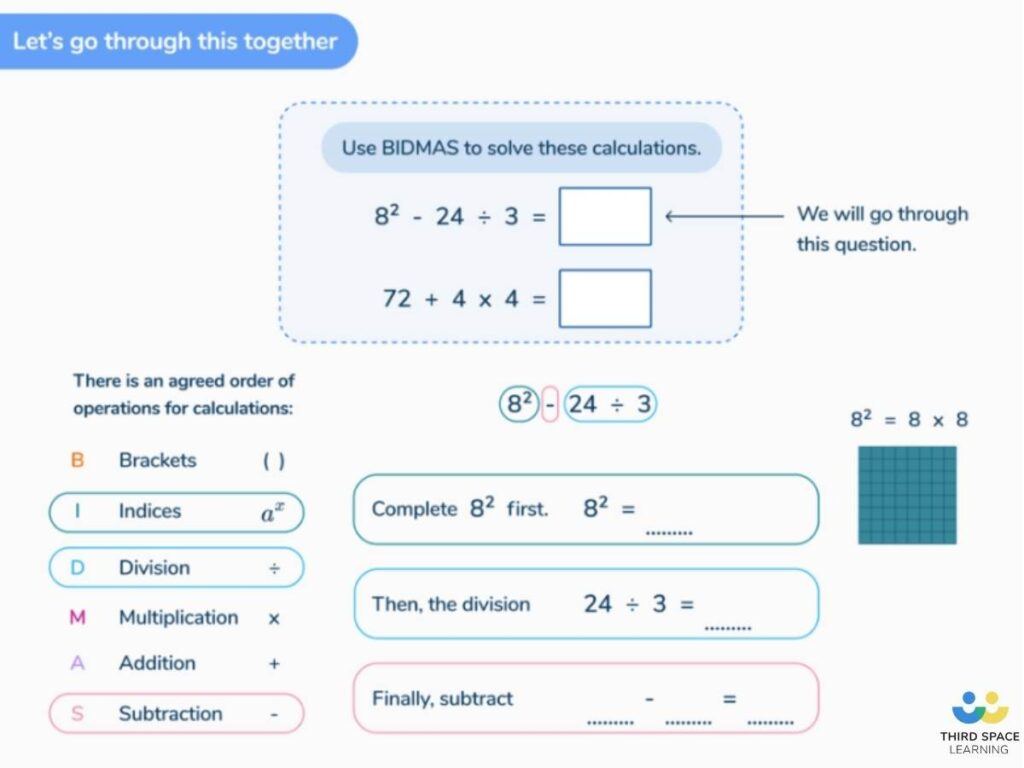
Example 1: 50 – 4² x 3

Worked solution: 

1. Brackets
   There are no brackets in this question.
2. Powers Of (or Indices in BIDMAS)
   4² is 16. The question now becomes 50 – 16 x 3.
3. Division and Multiplication
   16 x 3 = 48
4. Addition and Subtraction
   50 – 48 = 2

The correct answer is 2; without using the correct order of operations, this question would be incorrectly calculated as 102 (50 – 16 is 34, 34 x 3 = 102).

Example 2: 36 + (28 ÷ 7) – 18

Worked solution: 

1. Brackets
   Solve inside brackets first: 28 ÷ 7 = 4
2. Powers Of (or Indices in BIDMAS)
   There are no indices in this question.
3. Division and Multiplication
   There is no division or multiplication outside the brackets in this question.
4. Addition and Subtraction
   The question now reads 36 + 4 – 18. Addition and subtraction can be done in any order: if we did the addition first (36 + 4 = 40) and solved the calculation from left to right, then 40 – 18 = 22. If we did the subtraction first (4 = 18 = -14) and then the addition, then 36 + -14 = 22. 

KS2 BODMAS questions

Primary pupils aren’t introduced to the order of operations until their Year 6 maths lessons. The National Curriculum states that in the number (addition, subtraction, multiplication and division) unit, Year 6 pupils “should be taught to use their knowledge of the order of operations to carry out calculations involving the four operations”. In the non-statutory guidance, the NC suggests that “pupils explore the order of operations using brackets; for example, 2 + 1 x 3 = 5 and (2 + 1) x 3 = 9.”

Year 5 number (multiplication and division): recognise and use square numbers and cube numbers, and the notation for squared (²) and cubed (³)

BODMAS questions Year 6

• 2³ + 5 x 4

2 cubed = 2 x 2 x 2 = 8. Multiplication comes next (5 x 4 = 20), then 8 + 20 = 28.

• 60 – 21 ÷ 3

Completing the operations in the correct order (division then multiplication) would result in the correct answer of 53. However, this is a good question to assess the children’s knowledge of BODMAS because the answer would also seem ‘easy’ if completed incorrectly, as 60 – 21 = 39, which is easily divided by 3 (13). 

• 36 ÷ (11 – 7)

The answer is 9.

BODMAS SATs questions

Since the introduction of the new curriculum in 2016, BODMAS questions have appeared a number of times throughout the SATs papers: notably though, it is only in 2019 that questions requiring BODMAS have shown up in both the reasoning and arithmetic papers; prior to this, they were only in the arithmetic tests.

SATs arithmetic questions and answers (each worth 1 mark)

SATs year	Question	Answer	Answer without BODMAS (common misconception)
2016	60 – 42 ÷ 6	53	3
2016	32 + 10 =	19	Not a BODMAS misconception, but some children misunderstand 32 to mean 3×2 as opposed to 3×3
2017	50 + (36 ÷ 6) =	56	86/6 or 14r2
2018	92 – 36 ÷ 9 =	77	5
2018	62 + 10 =	46	Not a BODMAS misconception, but some children misunderstand 62 to mean 6×2 as opposed to 6×6
2019	60 ÷ (30 − 24) =	10	-22

SATs 2019 reasoning questions and answers

Question	Answer	Answer without BODMAS (common misconception)
A theme park sells tickets online. Each ticket costs £24. There is a £3 charge for buying tickets. Which of these shows how to calculate the total cost, in pounds? Choose one. a) number of tickets x 3 + 24 b) number of tickets x 24 + 3 c) number of tickets + 3 x 24 d) number of tickets + 24 x 3	b)	Any of the others
Write the missing number. 6 + 2 x 2 – ? = 6	4	10

Third Space Learning’s online one-to-one SATs revision lessons cover the topic of BODMAS (BIDMAS) and the order of operations, providing students with practice questions to help cement understanding of the concept and prepare them for the SATs exams. Third Space Learning also offers a wide variety of worksheets including BODMAS worksheets to support students’ and teachers’ preparation for SATs.

Simple BODMAS questions

The simplification of BODMAS questions can be achieved by limiting the number of operations used or making the calculations themselves simple. Another way to simplify BODMAS questions (although this doesn’t directly assess children’s knowledge of the order of operations) is by ensuring that there is only one possible answer even without the use of BODMAS.

• (4 x 3) + 12

The multiplication should be completed first here, whether the brackets are present or not. Mathematically, the presence of the brackets is unnecessary, but it is useful to expose children to this notation. The answer is 12.

• 20 – 9 ÷ 3

Hopefully children will realise that without BODMAS, this becomes overly complicated (11 ÷ 3 is tricky to calculate) – when the order of operations is completed correctly, the answer is 17.

• 2² + 5

This would be difficult to answer incorrectly – even if the squared notation is misunderstood as doubling instead of multiplying by itself, the answer remains the same. I’m also not sure how you would do these operations in the wrong order. The answer is 9.

Difficult BODMAS questions

• Put brackets into this expression to make it correct: 10² ÷ 10 ÷ 10 ÷ 10 ÷ 10 = 100

There are many different answers to this question, including brackets within brackets:
10² ÷ (10 ÷ 10) ÷ (10 ÷ 10) = 100
10²  ÷ ((10 ÷ 10) ÷ 10)) ÷ 10 = 100
(10² ÷ 10) ÷ ((10 ÷ 10) ÷ 10) = 100
10² ÷ (10 ÷ (10 ÷ (10 ÷ 10))) = 100
10² ÷ (10 ÷ (10 ÷ 10) ÷ 10) = 100
10² ÷ (10 ÷ 10 ÷ (10 ÷ 10)) = 100

• Here are five numbers: ½     1½     2     2½     3½
  Use three of the numbers to make this calculation correct: (? + ?) x ? = 10

Whilst the BODMAS element of this isn’t too difficult, it is made more complex with the inclusion of fractions. There are two possible answers to this question:
(1½ + 3½) x 2
(½ + 3½) x 2½  

• Write the correct missing operation to make the calculation correct: 18 __ 3 x 5 = 30

18 ÷ 3 x 5 = 30

• Write the missing numbers:
  a) 48 ÷ (19 – ?) = 4
  b) ? + 6 x 8 = 56

In a), we know the brackets must be solved first. Looking at 48 ÷ ? = 4, we can see the missing amount must be 12, and so the calculation in the brackets must also equals 12. The answer is therefore 48 ÷ (19 – 7) = 4
In b), we know the multiplication must be solved first, and 6 x 8 = 48. The question then becomes ? + 48 = 56, which is 8, so the answer is 8 + 6 x 8 = 56.

BODMAS beyond primary 

Whilst there isn’t a direct mention of the ‘order of operations’ in the secondary maths curriculum, the KS3 maths and GCSE maths curriculums do require pupils to “use conventional notation for the priority of operations, including brackets, powers, roots and reciprocals” and to “recognise and use relationships between operations including inverse operations”.