8 Long Division Examples And How To Solve Them: Explained For Primary School
Long division examples are a great way to introduce and teach long division to Year 6. Due to the number of steps involved, it can be tricky for students to get their head around the method. In this article, we provide you with long division examples to practise with KS2 primary school pupils, plus expert guidance on how to solve them.
When teaching a new mathematical concept, worked examples are helpful in the same way that a ‘WAGOLL’, or model text, is helpful in writing lessons – children can see what the end result should look like. They can be used as a success criteria for mathematical problem solving- and long division is no exception.
How to work out long division examples
In any division, the first number (the amount being divided) is called the dividend; the second number (whatever the dividend is being divided by), is called the divisor; the answer is called the quotient. Long division is typically used when dividing larger numbers where the divisor is a two-digit number, although it can also be used with one-digit divisors.
There are five steps that can be used to simplify the long division method. These long division steps are:
- Divide
- Multiply
- Subtract
- Bring the next digit down
- Repeat
3 Long Division Worksheets For Year 3-6 Classes
This resource contains three ready-to-use worksheets to build up the long division skills of your pupils, from 1 digit up to listing multiples!
Download Free Now!Before beginning long division questions, it is helpful to list 9 multiples of the divisor to reduce the cognitive demand when working through the division method. Listing multiples can be done through repeated addition or partitioning (partition the tens and ones, list the multiples of each and then add each constituent part).

Long division example step by step
See how the five division steps are then applied using this example below (this layout is also called the bus stop method):
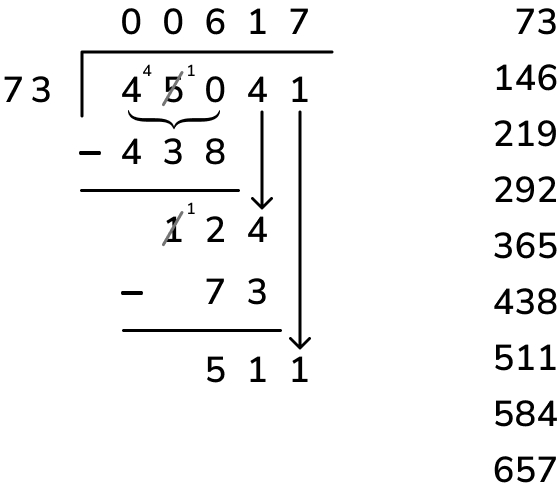
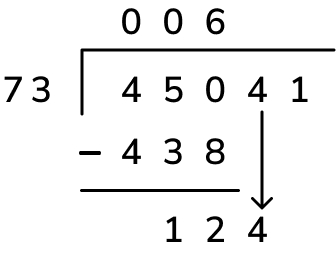
1. Divide: Starting with the first digit of the dividend, divide 4 ten thousands by 73. We cannot do this, so a 0 is placed above the 4 and instead we see the 4 ten thousands as 40 thousands alongside the 5 thousands (the next digit of the dividend).
Now, divide 45 thousands by 73, which also can’t be done, so we place another 0 above the 5 and see the 45 thousands as 450 hundreds. We can finally do 450 hundreds divided by 73, which is 6. This digit is placed above the 0 tens and becomes the first digit of the quotient.

2. Multiply: We need to calculate the remainder for this first step of the division – to do this, firstly multiply the first digit of the quotient, 6 hundreds, by the divisor, 73, to get 438 hundreds (this is where our list of multiples really helps). Place this underneath the dividend, making sure to align the place values correctly.
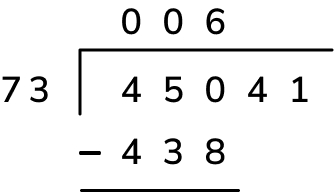
3. Subtract: To finish calculating the remainder for this first step of the division, finally subtract 438 hundreds from 450 hundreds to get 12 hundreds.
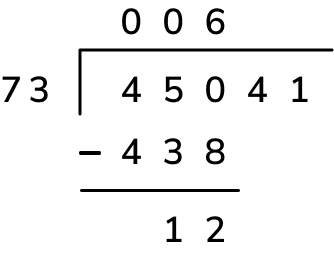
4. Bring the next digit down: In short division, we would place the remainder from each step before the next digit in the dividend – in this case, the 12 would be written to the top left of the digit ‘4’ to read 124. In long division, we just bring the next digit of the quotient down – this achieves the same thing but is just a bit easier to read!
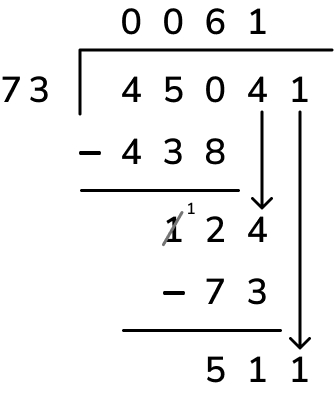
5. Repeat: Now we start the division process again from…
Step 1: divide (divide 124 tens by 73 and place the answer, 1 ten, in the quotient);
Step 2: multiply (multiply the next digit of the quotient, 1 ten, by the divisor, 73, and place the answer, 73 tens, underneath the 124 tens);
Step 3: subtract (finish calculating the remainder to this next step by subtracting 73 tens ones from 124 tens to get 51 tens);
Step 4: bring the next digit down (51 tens plus 1 one becomes 511 ones)
Step 5: repeat (divide 511 ones by 73 to get 7 ones and place this in the quotient as the last digit; multiply 7 ones by 73 to get 511 ones; subtract this from 511 ones to calculate the remainder, which is 0; there is now no next digit to bring down so, as the remainder is now 0, the calculation is complete)
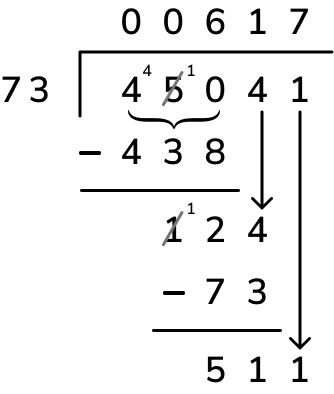
This example has a whole number quotient, but the long division method can be done with remainders.
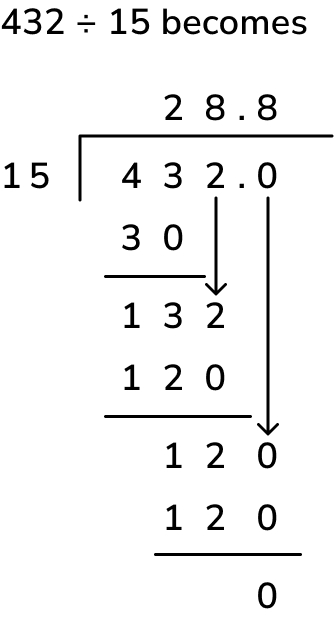
This example from the national curriculum shows how it would be laid out with a decimal remainder (when calculating the remainder, don’t forget to include the decimal point in the quotient as well as in the dividend).
Long division examples
Providing worked examples is helpful when introducing new mathematical concepts to children. Children can use these as success criteria for their own work. In TSL’s one-to-one tutoring sessions, tutors model new mathematical methods step by step to support and scaffold children’s learning. We find this is a great way to help students understand and practise the steps involved in long division.
Below, we provide a range of worked long division examples to suit your pupil’s needs. You can learn more about Third Space Learning and our maths interventions for KS2 pupils here.
For more support teaching the long division method, read our blog here.
Year 6 long division examples
As per the national curriculum, children aren’t required to do long division until Year 6. Here are some worked examples of long division problems taken from past SATs papers.
1. 8,051 ÷ 83
This question appeared on a recent SATs arithmetic paper. Don’t forget to list the first 9 multiples of 83 to help you solve it.
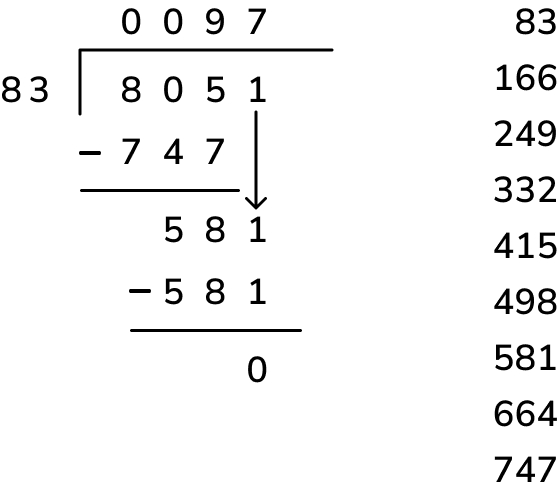
Step by step long division
- We cannot divide 8 thousands by 83
- Write zero in the thousands place of your answer line
- 80 hundreds cannot be divided by 83
- Write zero in the hundreds place of your answer line
- 805 tens divided by 83 is 9 tens
- Write nine in the tens place of your answer line
- Subtract 747 tens (9 x 83) from 805 tens to get 58 tens
- Exchange the 58 tens for ones so now we have 581 ones
- 581 ÷ 83 = 7
- Write 7 in the ones place of your answer line
- Subtract 581 (7 x 83) from 581 to get zero. You have no remainders.
- Check your answer – 83 x 97 = 8051
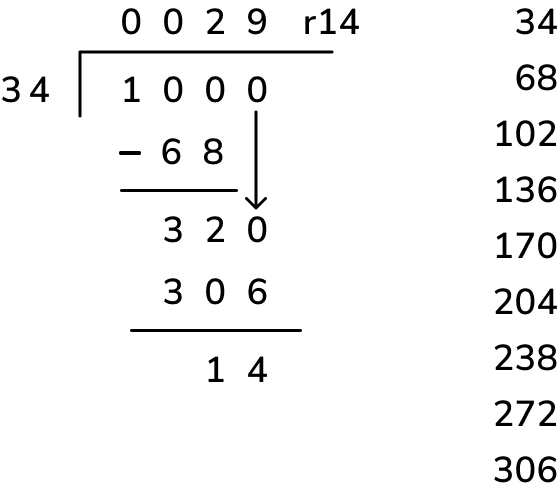
2. Adam is making booklets. Each booklet must have 34 sheets of paper. He has 2 packets of paper. There are 500 sheets of paper in each packet. How many complete booklets can Adam make from 2 packets of paper?
This long division word problem appeared on a recent SATs reasoning paper. 2 packets of 500 sheets = 1,000 sheets. 1,000 ÷ 34 = 29 complete booklets
Easy long division examples
1. Eggs are put in trays of 12. The trays are packed in boxes. Each box contains 180 eggs. How many trays are in each box?
You could use long division for 180 ÷ 12 as we’re dividing by two digits, but in this case it could be just as simple to use multiples of 12 to work it out. We know 12 x 5 = 60, and there are 3 lots of 60 in 180, so there must be 15 lots of 12 in 180. The answer is therefore 15 trays.
2. A lottery donates £504 to 21 different charities. How much does each charity get?
Whilst 504 ÷ 21 may seem tricky at first glance, it’s actually fairly simple as the divisor is an ‘easy’ number to list multiples of – children may be able to complete it without having to list the multiples first and by calculating them mentally instead.
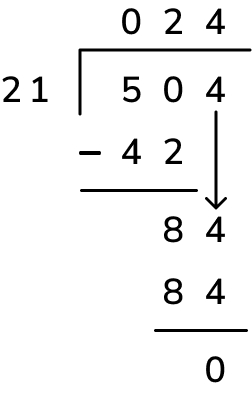
Hard long division examples
1. A grocer needs to order 1,176 apples. Apples are sold in boxes containing 28 trays, with 14 apples on each tray. How many boxes of apples does the grocer need to order?
28 trays each with 14 apples = 28 x 14 = 392 apples. We could then do 1,176 ÷ 392, but this is quite a tricky calculation! It would be better to do the long division in two chunks – first dividing by 28, then by 14 (or the other way round – the answer would be the same!) 1176 ÷ 28 = 42, then 42 ÷ 14 = 3, so the grocer would need to order 3 boxes of apples.
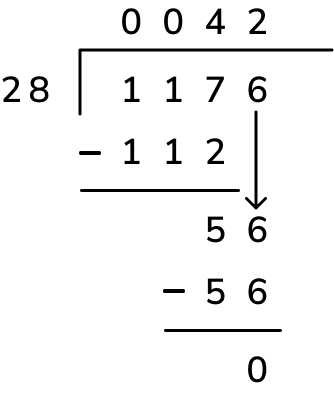
2. A factory makes 4,923 teddy bears, and the bears are packed in boxes of 37. How many bears are left over?
4,923 ÷ 37 = 133r2, so there will be 2 bears left over.
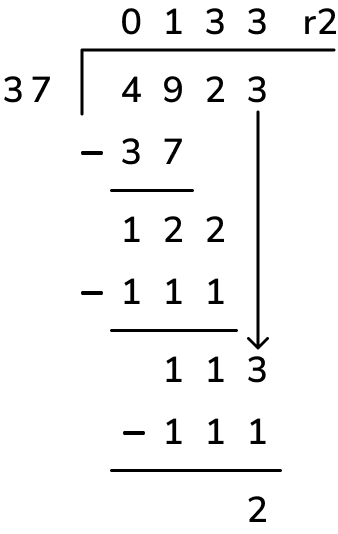
3. 427 children visit a castle. They go in groups of 15. One group has less than 15. Every group of children has one adult with them. How many adults will need to go?
427 ÷ 15 = 28r7, as shown below. This means there are 28 ‘full’ groups (of 15 children) and one more group with only 7 children. There are therefore 29 groups overall, so 29 adults would be required to go. Read more here about how to complete division with remainders.
For more long division questions and long division worksheets to support your teaching, check out our blogs.
Top tips for working through long division examples
- List 9 multiples of the divisor before beginning the division to reduce cognitive load
- Ensure you align the place values correctly (each digit of the quotient going above the appropriate digit of the dividend)
- During the ‘divide’ step, if at any point your divisor will not fit into the dividend, don’t forget to include the 0!
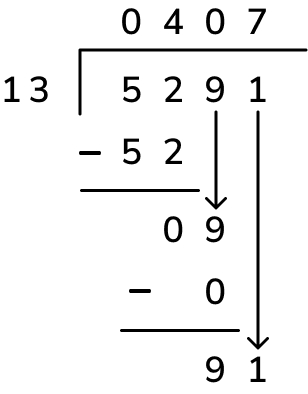
In the example below, we’ve firstly correctly identified that 52 hundreds divided by 13 is 4 hundreds. This gives us a remainder of 0, but when we bring the next digit down it makes 9 tens. We can’t divide 9 tens by 13, so here, we’ve incorrectly brought down the next digit as well to make 91 ones. 91 ones ÷ 13 is 7, but this 7 has been placed as the wrong digit in the quotient.
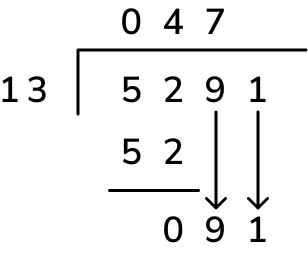
This is what the division should have looked like – after 52 hundreds ÷ 13 = 4 hundreds with 0 remainder, 9 tens divided by 13 = 0, so the 0 has to be placed as the next digit of the quotient (above the 9 in the dividend).
We can then continue with the method – multiply (0 tens x 13 = 0 tens), subtract (9 tens – 0 tens = 9 tens) and bring the next digit down (1 one, to make 91 ones). This takes us to the final step now (91 ones ÷ 13 to get 7 ones) which reaches the correct answer of 407, as opposed to 47 in the misconception above.
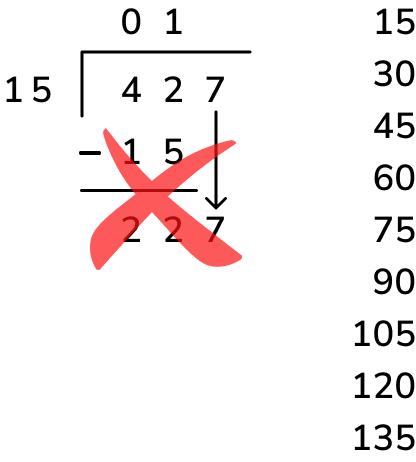
During the ‘subtract’ step, if the result of your subtraction (once you’ve brought down the next digit of the dividend) is bigger than 9 multiples of the divisor, something has gone wrong! In the example below, we’ve incorrectly calculated that 42 tens divided by 15 is only 1 ten. This gave us a remainder of 27 tens + 7 ones, which is 277 ones – we can fit way more than 9 groups of 15 into 277 ones, so we have gone wrong somewhere!
The first digit of the quotient should actually be 2 as 42 tens divided by 15 is 2 tens with 12 tens remaining, as shown below.
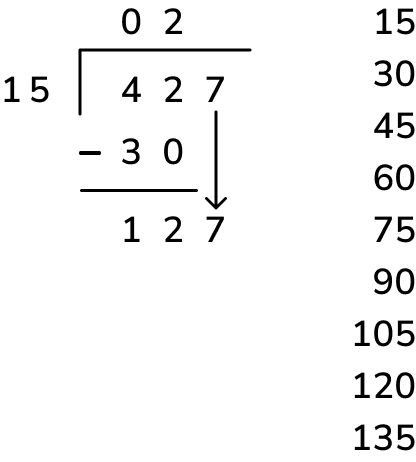
- Use the inverse to check your answer at the end: in a division without a remainder, simply multiply the quotient by the divisor and you should get the dividend (e.g. if you calculate that 1,176 ÷ 28 = 42, then 42 x 28 should = 1,176).
In a division with a remainder, multiply the quotient by the divisor and then add the remainder – the result should, again, be the dividend (e.g. if you calculate that 427 ÷ 15 = 28r7, then 28 x 15 + 7 should = 427)
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.