What Is Bus Stop Method: Explained for Primary School
The bus stop method of division is taught when children are in KS2.
What is the bus stop method?
The bus stop method is a quick, formal written method of division. It is named after its ‘bus stop’ appearance. The dividend (number being divided) is inside the ‘bus stop’; the divisor (what the dividend is being divided by) is outside the ‘bus stop’; and the quotient (the answer, or how many times the divisor fits into the dividend) is on top of the ‘bus stop’.
- What is the bus stop method?
- The bus stop method for division step by step
- Examples of bus stop method in action
- Bus stop method division with remainders
- When do children learn about the bus stop method in the national curriculum?
- How does the bus stop method of division relate to other areas of maths?
- The bus stop method of division in real life
- 6 bus stop method practice questions and answers
The bus stop method for division step by step
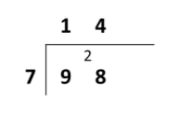
Bus stop division begins at the largest place value (the left), unlike the formal methods of addition, subtraction and multiplication where the procedure begins from the smallest place value (the right).
Let’s take the example 98 ÷ 7, such as the first example in the national curriculum appendix, to explore the bus stop method for division step by step.
- Starting on the left we divide 9 tens by 7 tens.
- 7 tens goes into 9 tens once with 2 tens left over, so we place a 1 on top (which is the first digit of the quotient)
- Next, we regroup the 2 tens into 20 ones and alongside the next number, the 8 ones which now becomes 28 ones.
- Finally, 28 ones (or just 28) ÷ 7 ones is 4, so 4 becomes the last digit of the quotient.
- Therefore, our answer is 14.
Read more: What Is Division? Explained For Primary School
Examples of bus stop method in action
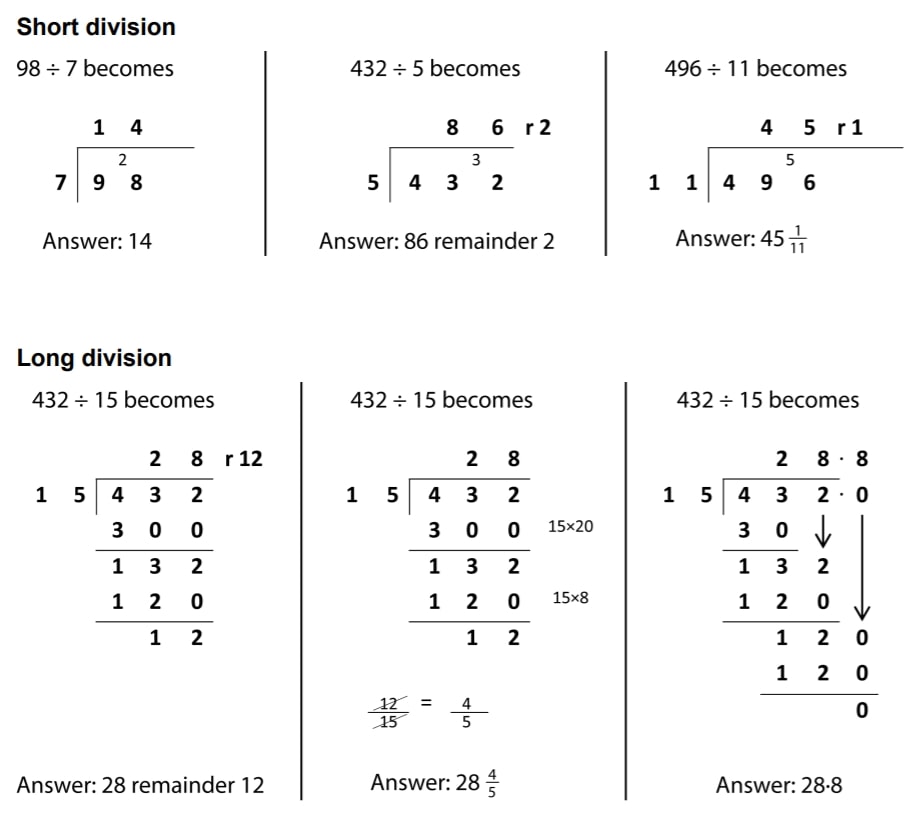
The bus stop method is demonstrated in the national curriculum appendix 1. Short division is a compacted version of long division, but it is still the same mathematical process. It is generally used when the divisor is a 1-digit number. The bus stop method is often used for division problems involving two and three-digit numbers.
3 Long Division Worksheets for Year 3-6 Classes
Download free, printable division worksheets on the bus stop method. This learning resource contains a variety of questions suitable for years 3-6 to practise applying the bus stop method.
Download Free Now!Bus stop method division with remainders
Bus stop division with remainders can be expressed in three ways as demonstrated in the long divisions above:
- a simple remainder
- a fraction
- a decimal
The first two long divisions shown are examples of a method informally known as ‘chunking’.
The long division method is generally used when the divisor is a 2-digit number (and when the dividend is a 3-digit number or higher).
The third example in the top row above demonstrates dividing by a 2-digit number, 11, using the short division method. This is because the multiples of this divisor (the 11 times table) are relatively simple to calculate.
When do children learn about the bus stop method in the national curriculum?
The bus stop method is the informal name for the formal method of division. It isn’t officially introduced until Year 5, but it is mentioned in the non-statutory guidance of the national curriculum in lower KS2:
- In Year 3, “pupils develop reliable written methods for multiplication and division, starting with calculations of two-digit numbers by one-digit numbers and progressing to the formal written methods of short multiplication and division”.
- In Year 4, “pupils practise to become fluent in the formal written method of short multiplication and short division with exact answers”.
Year 5:
- divide numbers up to 4 digits by a one-digit number using the formal written method of short division and interpret remainders appropriately for the context
Year 6:
- divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context
- divide numbers up to 4 digits by a two-digit number using the formal written method of short division where appropriate, interpreting remainders according to the context
For support on how to teach division to your KS2 pupils, read our comprehensive guide developed by expert maths practitioners.
How does the bus stop method of division relate to other areas of maths?
Children will often come across division questions that may also involve one of the other four operations – these are called multi-step problems, as they require the children to complete more than one mathematical process to solve them.
The bus stop method may be useful in these situations, particularly where large numbers are involved. Whilst the concept of division will be encountered in many other areas of maths (such as fractions), the bus stop method itself will only be explicitly taught – and possibly only required – during a division topic.
The bus stop method of division in real life
The bus stop method may be useful when sharing or grouping larger numbers than could be calculated mentally (e.g. £41,267 shared between 7 people).
6 bus stop method practice questions and answers
- 1,645 ÷ 7
Answer: 235 - What is the missing number? 3,170 ÷ __ = 5
Answer: 634 - 3,312 ÷ 92
Answer: 36 - A farmer is packing eggs. Each box holds six eggs. The farmer has 980 eggs to pack. How many boxes can the farmer fill using 980 eggs? How many eggs will be left over? (2018 SATs)
Answer: 163 boxes and 2 left over - A box contains 2.6 kg of washing powder. Jack uses 65 grams of powder for each wash. He uses all the powder. How many washes did Jack do? (2018 SATs)
Answer: 40 - A group of friends earns £80 by washing cars. They share the money equally. They get £16 each. How many friends are in the group? (2017 SATs)
Answer: 5
For more resources, take a look at our collection of division worksheets.
Start at the biggest place value – in this case, 9 tens. Start with calculating how many lots of 7 tens go into 9 tens – the answer is 1 with 2 remaining, so the 1 goes above the 9 and the 2 goes before the 8. The two represents 2 tens and the 8 represents 8 ones, so this number is now 28. Finally calculate how many lots of 7 go into 28 – the answer is 4, so the 4 goes above the 8. 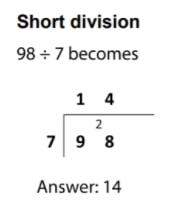
Yes, long division using the formal written method of long division is the same as the bus stop method. See more long division examples here.
Read more:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.