Division Questions That Will Test Your Primary School Pupils
Division questions will appear throughout primary school as division is one of the four mathematical operations- addition, subtraction, multiplication and division. Children will encounter all four operations from as early as Year 1.
From experience, children seem to find division the trickiest to grasp. Here are some questions to use for division practice with children, plus expert guidance on how to solve them.
What are division questions?
Division questions can be standard arithmetic (e.g. 25 ÷ 5 or 3,426 ÷ 2) or can be presented as word problems which present a maths problem in a ‘real-life’ context. In this case of division, this will involve sharing or equal grouping and may require children to interpret the remainders appropriately, either by rounding up or down.
How to solve division questions
In a division calculation:
- The first number (the amount being divided) is called the dividend;
- The second number (whatever the dividend is being divided by), is called the divisor;
- The answer is called the quotient.
Division questions may be solvable mentally, perhaps using times table knowledge or place value knowledge. For example:
a) Mrs Patel has 16 sweets to share between 4 children. How many should each child get?
16 sweets ÷ 4 = 4 sweets each. Children should be able to use their times table knowledge to solve this.
b) A £283 bill at a restaurant has to be split between 10 people. How much should each person pay?
£283 ÷ 10 = £28.30 each. Children should be able to use their place value knowledge for this.
Other division questions may require the use of a formal written method, such as the bus-stop method.
c) A length of ribbon measures 28.8cm. It is cut into 6 equal pieces. How long is each piece?
28.8cm ÷ 6 = 4.8cm (see short division below).
All Kinds Of Word Problems Division
In this free resource, find over 40 word problems to extend your Year 3-6 pupils' reasoning skills and division abilities. Includes challenge questions for your highest attainers!
Download Free Now!Division questions KS2
Division questions will appear throughout KS2. However, as the formal method of division (commonly known as the bus stop method) isn’t introduced until Upper KS2, the division questions pupils will encounter will reflect this.
In Year 5, children begin with ‘short division’ (usually used when dividing by a single digit number). In Year 6, they will then learn a ‘long division method’ (usually used when dividing large numbers by a 2-digit number). They will also begin to work with division with remainders.
See below the table, which has been adapted from the national curriculum’s programme of study, that details the development of skills in multiplication and division throughout KS2.
| Year 3 |
|
| Year 4 |
|
| Year 5 |
|
| Year 6 |
|
If you’re looking for more information on how to teach division or how to plug pupil’s division knowledge gaps in interventions, read our articles written by maths specialists.

Division questions Year 4
1. 75 children take part in a quiz. There are 5 children in each team. How many teams are there altogether?
Answer: 75 children ÷ 5 = 15 teams
2. David wants to decorate some cakes. Each cake will have 3 cherries. David has 48 cherries. How many cakes can he decorate?
Answer: 48 cherries ÷ 3 = 16 cakes
3. John needs 18 balloons. The shop sells balloons in packs of 5. How many packs does he need to buy?
Answer: 18 balloons ÷ 5 = 3 packs with 3 left over, so John would need to buy 4 packs.
Division questions Year 5
1. I have 1 \frac{1}{2} litres of juice. I need to share it all equally between 6 glasses. How many millilitres of juice should I pour into each glass?
Answer: 1 \frac{1}{2} litres = 1,500ml. 1,500ml ÷ 6 = 250ml of juice in each glass
2. A school fair raises £5,168. The school keeps \frac{1}{4} of the money for new playground equipment. It gives the rest to charity. How much money does it give to charity?
Answer: £5,168 ÷ 4 = £1,292 kept by the school. They give the rest to charity, which is £5,168 – £1,292 = £3,876 to charity.
3. Sahil wants to walk a long distance, for charity, over 6 weekends. The total distance Sahil wants to walk is 293km. Approximately how far should he walk each weekend?
Answer: 293km ÷ 6 = 48r5 km. We can round this up to 49km – if he walks 49km each weekend he will definitely meet his target!
Division questions Year 6
1. A carpet is 190cm in length and 91cm in width. Ben makes a one-tenth scale model of the carpet. What is the length and width of the scale model?
Answer: 190cm ÷ 10 = 19cm (length); 91cm ÷ 10 = 9.1cm (width).
2. The International Space Station orbits the Earth at a height of 250 miles. What is the height of the International Space Station in kilometres? Use 8 kilometres equals 5 miles.
Answer: 250 miles ÷ 5 = 50 miles. 50 miles x 8 = 400km.
SATs questions on division
The KS2 SATs papers are designed using the Key Stage 2 mathematics test framework. The content domains below are an example of some based around division – this content could appear in any SATs paper as these assessments test on content from the whole of KS2, not just Year 6.
Below are three SATs division questions and their relevant content domain.
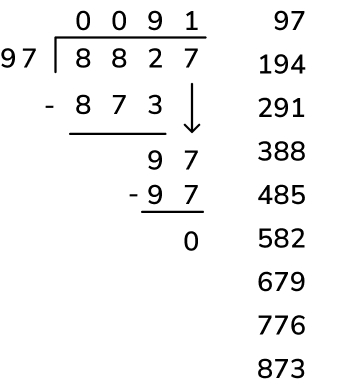
1. 8827 ÷ 97 (content domain 6C7b)
Answer: 91. The multiples here could be listed more quickly (than by using repeated addition or partitioning) by adding 100 and subtracting 3 each time.
2. 3 pineapples cost the same as 2 mangoes. One mango costs £1.35. How much does one pineapple cost? (content domain 6R1/5M9a)
Answer: 2 mangoes = £1.35 x 2 = £2.70 (the same as 3 pineapples). £2.70 ÷ 3 = 90p, which is the cost of 1 pineapple.
3. Amina posts three large letters. The postage costs the same for each letter. She pays with a £20 note. Her change is £14.96. What is the cost of posting one letter? (content domain 6C8/5M9a)
Answer: £20 – £14.96 = £5.04 (the cost of three letters). £5.04 ÷ 3 = £1.68, which is the cost of one letter.
Simple questions on division
1. 8 metres of rope is cut into 4 equal lengths to make skipping ropes. How long is each skipping rope?
Answer: 8m ÷ 4 = 2m
2. Tick two numbers which divide by 5 with no remainder: 9, 50, 12, 35, 31, 57
Answer: 50 and 35 – both are in the 5 times table as they end in either a 0 or 5
3. 28 children go swimming in groups of 4. How many groups will there be?
Answer: 28 children ÷ 4 = 7 groups
Hard questions on division
2. 999 will divide exactly by 37. There is no remainder.
a) Write down the remainder when 1000 is divided by 37.
b) Write down the remainder when 998 is divided by 37.
c) Write down a multiple of 37 that is bigger than 1,000.
Answers:
a) As 1,000 is only 1 more than 999, the remainder will be 1.
b) As 998 is only 1 less than 999, the remainder will be 1 less than the divisor (37), so the remainder is 36.
c) As 999 is a multiple of 37, if we add 37 we will get another multiple of 37. We can work out that 999 + 37 = 1,036, which is a multiple of 37 bigger than 1,000
2. Write the missing number: 12.5 ÷ ___ = 7.5 ÷ 1.5
Answer: 7.5 ÷ 1.5 = 5 – we can work this out by counting in multiples of 1.5 until we reach 7.5 (5 lots of 1.5 is 7.5). We could also make each number 10 times bigger to make it ‘easier’ to solve as the answer will be the same: 75 ÷ 15 = 5. We are now left with 12.5 ÷ ___ = 5. When the divisor is missing, we can divide the dividend by the quotient instead to reach the answer. 12.5 ÷ 5 = 2.5, so the missing number is 2.5.
3. A bus company has 62 buses. On average, each bus travels 19 miles on a gallon of fuel and goes 284 miles each day. The bus company says it needs about 900 gallons of fuel every day. Approximate these numbers and make an estimate to show whether what the company says is about right.
Answer: To approximate, we could round 19 miles to 20 and 284 miles to 280. 280 miles per day ÷ 20 miles per gallon = 14 gallons per minibus per day. For approximately 60 minibuses (we’ve rounded 62 to 60 to approximate), this would be 14 x 60, which would be 840 gallons. This is close to 900 gallons so the company is about right.
Looking for more resources to support your teaching of division? See our blog on division worksheets.
Read more:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.