11 Common Mistakes On The SATs Year 6 Arithmetic Test And How To Fix Them
Ask any Year 6 teacher which KS2 SATs test is the easiest to ‘pick up points’ on, and they’ll most likely say the SATs Year 6 arithmetic test. From personal experience, it tends to be the most popular amongst children too – possibly because the answers are so clearly either right or wrong.
However, it is so common for children to demonstrate a much higher level of maths and command of the national curriculum during lessons, then perform much more poorly than expected on the KS2 arithmetic paper. The children have 36 questions and 40 marks to prove their arithmetic skills, and it is so easy to make ‘silly mistakes’ on questions that you know they know how to solve!
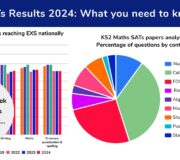
In my experience, the most common errors on the Key Stage 2 SATs arithmetic paper seem to be made in the 10 mathematical areas listed below (plus those marks painfully lost on mistakes that have nothing to do with the children’s maths skills, such as missing out questions!).
In many of these Year 6 arithmetic questions, there is more than one way of solving them – competent mathematicians will know this and be able to choose the most efficient method. However, those children who struggle a little more may benefit from knowing one consistent method for each type of question, as I discuss in the topics below.
SATS 2025: STAY UP TO DATE
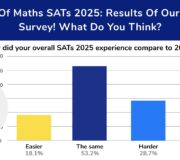
Join our email list to stay up to date with the latest news and free resources for SATs 2025. As usual our expert teachers will be on hand to provide one to one tuition support, revision resources, expert analysis on papers, 2025 SATs teacher survey results and the 2025 SATs results.
Year 6 Worked Examples Pack 1
This free resource includes practice reasoning papers, arithmetic papers and answer sheets to help prepare your students for the Key Stage 2 SATs.
Download Free Now!11 common errors on the SATs arithmetic paper
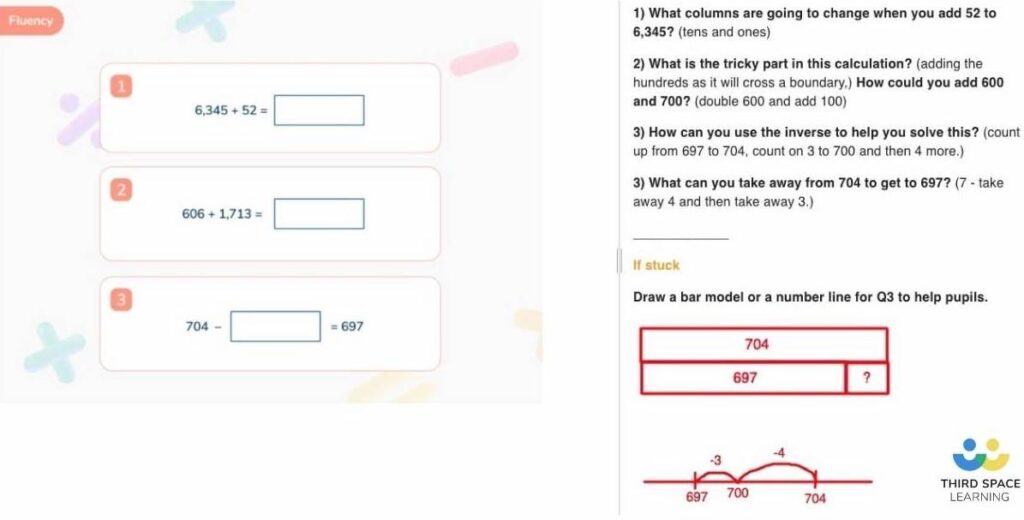
1. Missing number addition or subtraction
Real examples from past KS2 Maths SATs Year 6 arithmetic test
- ___ + 5 = 341
- ___ – 100 = 1,059
- 602 – ___ = 594
Common mistake
Not understanding when to use the inverse.
Try this…
Represent each question as a bar model to consolidate when to use the inverse (as in examples 1 and 2). Also try examples with the equals sign at the start of the equation (e.g. 245 = ___ + 23) as children most commonly see these questions with the ‘answer’ (the sum or the difference) at the end of the equation.
During a Third Space Learning online one-to-one SATs revision lessons, tutors pre-empt the questions students may have difficulty answering. The tutor then gives prompts to the student to help support them in answering the question. We provide our tutors with teaching notes and suggestions on ways to best support students.

Unlimited primary maths tutoring with Skye, the voice-based AI maths tutor.
Built on the same principles, pedagogy and curriculum as our traditional tutoring, but with more flexibility, reach and lower cost.
Join the schools already helping hundreds of primary pupils nationwide with Skye’s one to one maths tutoring.
Watch Skye in action2. Multiplication
Real examples from past SATs Year 6 arithmetic test
- 5,413 x 86
- 71 x 46
- 14 x 100
Common mistake
For examples 1 and 2: omitting a 0 as the place value holder on the second line of the long multiplication method. For example 3: choosing long multiplication instead of moving the place value digits!
Our SATs revision lessons ensure pupils are always thinking about the ‘value’ of the digits when solving calculations and we encourage pupils to consider if they can complete the calculation in their head before resorting to a formal method.
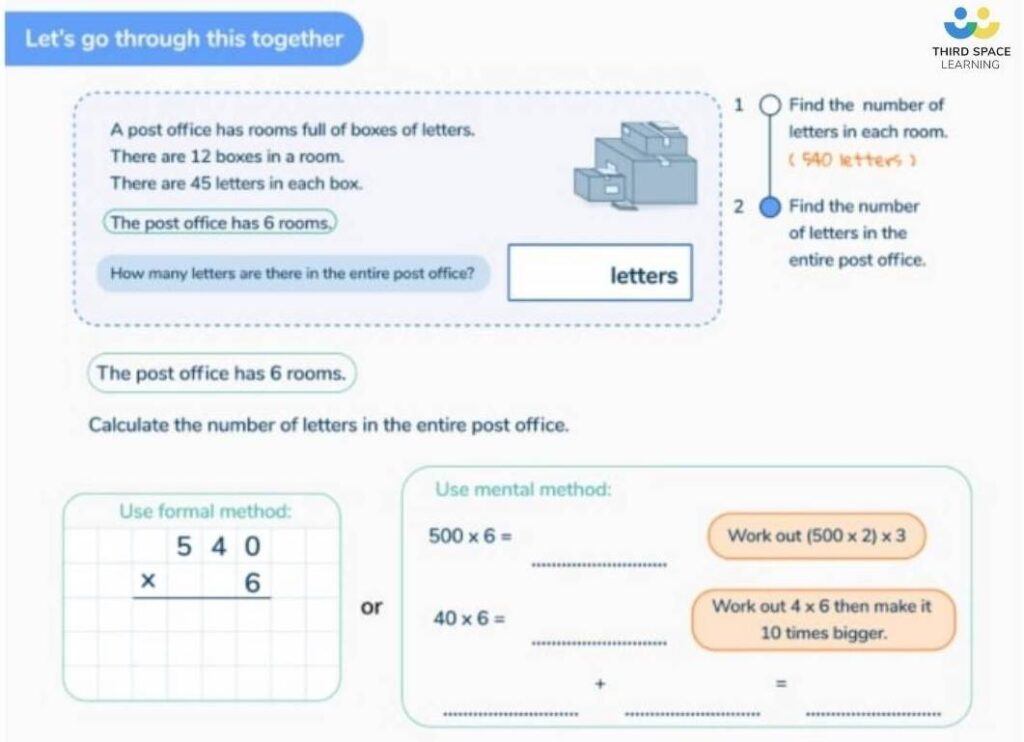
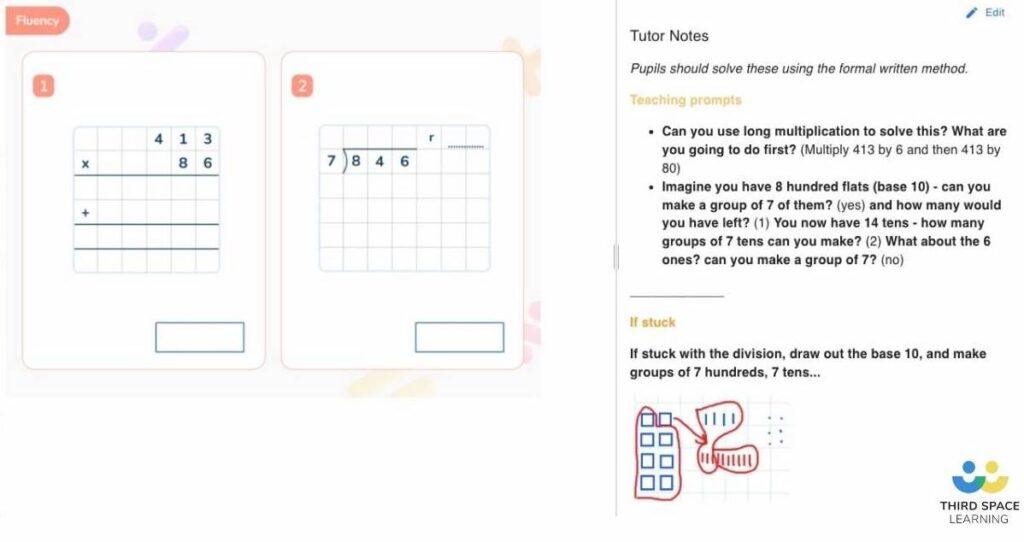
Try this…
Practise writing out the long multiplication in 2 different colours, one for each digit of the 2-digit multiplier. Have the children put the 0 in automatically with the 2nd colour before they even begin calculating.
Try examples with the 2-digit multiplier presented first (e.g. 67 x 543) as children most commonly see these questions with the bigger number first.
3. Division
Real examples from past SATs Year 6 arithmetic test
- 8,051 ÷ 83
- 1,210 ÷ 11
- 60 ÷ 15
- 0.9 ÷ 100
Common mistake
For example 1: minor inaccuracies along the way which result in an incorrect answer. For examples 2-4: not recognising that these can be completed mentally (how many times have you seen children use the bus-stop method / formal written method for questions like these?!)
Try this…
Encourage children to work out if they can use their times tables or place value knowledge before they attempt a formal division method. For questions like the first example, try the long division method. If the children have spare time to ‘check through’, they could use the inverse here (multiplication) to check their answers.
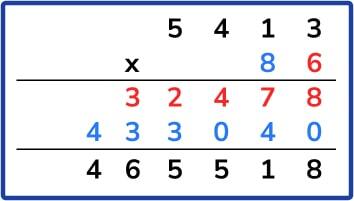
4. Decimal addition and subtraction
Real examples from past SATs Year 6 arithmetic test
- 9 – 1.9
- 5.87 + 3.123
Common mistake
Not aligning the decimal points or, in the case of example 1, writing the numbers the wrong way round because the second one ‘looks’ bigger as it has more digits (so 1.9 – 9).
Try this…
Practise using a different colour pen or pencil to write the decimal points and place value holder zeroes to reiterate the importance of their positioning.
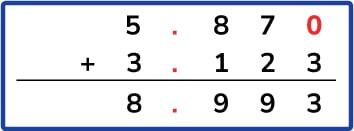
We also encourage students to think of decimals as money amounts. Students often seem better at decimals when they think about it in the context of money.
5. Decimal multiplication
Real examples from past SATs Year 6 arithmetic test
- 0.5 x 28
- 0.9 x 200
- 15 x 6.1
Common mistake
For examples 1 and 2: not recognising that these can be completed mentally (e.g. seeing 0.5 as ½ in example 1, so finding ½ of 28; using place value and times table knowledge for example 2). For example 3: lining up the place values ‘correctly’ as in addition or subtraction, such as below, reaching the incorrect answer of 915 as opposed to 91.5:

Try this…
Ask the children to ‘get rid’ of any decimals by multiplying them out first (in this case, multiplying by 10), then solve the multiplication before reversing your original action (in this case, dividing by 10). Another good way of checking is making sure that the answer has the same number of decimal places as the question, e.g. 42.3 x 1.6 (two decimal places in the question in total) = 67.68 (two decimal places in the answer).
6. Order of operations
Real examples from past SATs Year 6 arithmetic test
- 50 + 36 ÷ 6
- 92 – 36 ÷ 9
Common mistake
Not completing the operations in the correct order!
Try this…
A reminder of BIDMAS (brackets, indices, division and multiplication, addition and subtraction), encouraging children to circle the ‘most important’ operation, and then lots of practice!

7. Percentage of amount
Real examples from past SATs Year 6 arithmetic test
- 36% of 450
- 99% of 200
- 15% x 1,000
Common mistake
- For example 1: forgetting to divide by 100 at some point (if their chosen method is to find 1% first, and then 36%, which – in my opinion – is a quick and fail-safe method for any percentage of amount question!)
- For example 2: again, either forgetting to divide by 100 or failing to see a more efficient method – finding 1% and subtracting it from the whole.
- For example 3: not realising that ‘x’ means ‘of’ – or, again, forgetting to divide by 100!
Try this…
Lots of people teach the ‘bubble’ method for finding percentages, which often involves breaking percentages down into 50%, 10%, 5%, 1% (etc.) and adding together the relevant proportions (for example 1, this could mean finding 3 x 10% of 450, 1 x 5% and 1 x 1% in order to achieve 36% of 450).
Once children understand this method, I encourage them to always find 1% first and then to multiply it – this is often quicker and works for every single percentage of amount question.
To find 1%, you must divide by 100 and then multiply by the percentage you want to find. Because multiplication and division are commutative, these operations can be completed in any order, depending on the amount. For example, in the case of finding 41%, you could:

In application, choosing the most efficient method might look like this:
- 41% of 200: method A (200 ÷ 100 = 2; 2 x 41 = 82)
- 41% of 96: method B (41 x 96 = 3,936; 3,936 ÷ 100 = 39.36)
- 41% of 650: method C (650 ÷ 10 = 65; 65 x 41 = 2,665; 2,665 ÷ 10 = 266.5)
These methods are all chosen in order to avoid having to multiply decimals, which is where common mistakes often lie. It’s important to encourage children to check that their answer is sensible: firstly, that it shouldn’t be bigger than the amount in the question (as finding a percentage less than 100 means finding part of that whole); secondly, in the case of the question above, that their answer should be a bit less than half the amount, as 41% is less than 50%.
8. Adding and subtracting fractions and mixed numbers
Real examples from past SATs Year 6 arithmetic test
- 4⁄6 + 3⁄6
- 3⁄10 – 1⁄20
- 4 and 2⁄3 – 1 and 6⁄7
- 1 and 4⁄5 + 3⁄10
Common mistake
For examples 1 and 2: overcomplicating the common denominator (the number of times I’ve seen children convert 4⁄6 and 3⁄6 to 24⁄36 and 18⁄36! Of course they will achieve the same answer but there is more room for error here). For examples 3 and 4: making errors when crossing the whole.
Try this…
Encourage children to firstly check that the common denominator they want isn’t already one of the existing denominators (as it is in examples 1, 2 and 4 where one number is a multiple of the other). When adding and subtracting mixed numbers, for ease of a consistent method, children could always firstly convert mixed numbers to improper fractions – they can then leave their answers as an improper fraction (unless it simplifies to an integer).
Drawing a simple diagram can also help pupils visualise what they are trying to calculate.
9. Dividing fractions by integers
Real examples from past SATs Year 6 arithmetic test
- 3⁄5 ÷ 3
- 1⁄4 ÷ 2
Common mistake
For example 1: not recognising that three fifths shared into three equal parts will be one fifth (of course, 3⁄5 x 1⁄3 will still achieve the same answer). For example 2: dividing the denominator by the integer instead (in this case, to get 1⁄2).
Try this…
As with many of the other examples, competent mathematicians will be able to recognise when to use the most efficient method for each question. However, for the ease of a consistent method, encourage children to see dividing by an integer as equivalent to multiplying by its reciprocal – in other words, ÷ 2 = x½ ; ÷ 3 = x⅓ ; ÷ 4 = x¼ , and so on. The children then only need to multiply together the numerators and denominators, as they have learnt when multiplying proper fractions.
10. Multiplying fractions and mixed numbers
Real examples from past SATs Year 6 arithmetic test
- 5⁄6 x 540
- 1½ x 40
- 1¾ x 10
Common mistake
- For example 1: not recognising that this is the same as 5⁄6 of 540.
- For example 2: not recognising that this mixed number can be partitioned to (1 x 40) + (½ x 40) because ½ of 40 is easy to calculate (as opposed to example 3 which may be easier to convert to an improper fraction and solve as 7⁄4 x 10⁄1).
- For both examples 1 and 2: depending on the method, forgetting to simplify the answer to an integer (i.e. the answer of 120⁄2 would not be accepted for example 2)!
Try this…
Encourage children to work out if the denominator is a factor of the integer – if it is, it is like solving a fraction of an amount (as in examples 1 and 2). If not, the mixed number could be converted to an improper fraction in order to solve it more easily (as in example 3).
11. Clerical errors
- Misreading the operation (usually addition as subtraction or vice versa)
- Omitting decimal points
- Missing out questions
- Missing out WHOLE PAGES!
- Illegible digits (usually 6s as 0s and vice versa, or 7s as 1s)
- Getting the answer correct in the working out box but not copying it correctly into the answer box
Telling the children to ‘check through’ if they have spare time may not be very productive if the children haven’t been explicitly taught how to check and what exactly they’re looking for. An easy fix would be asking them to look for those clerical errors mentioned above – is there an answer in every question box and could someone else clearly read their answer?
Final SATs Year 6 arithmetic test preparation
With only a few weeks left until KS2 year 6 SATs, revision sessions would benefit from regular arithmetic practice tests, questions and worksheets. Mark any arithmetic practice or SATs practice papers as a class, looking over the mark scheme and answer sheet and ask the children to make note of the types of questions they still don’t understand and focus the revision around these.
Use these free resources such as our free SATs papers during your final SATs year 6 maths revision sessions to help your class prepare. Practice makes perfect!
More Year 6 SATs practice:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about year 6 sats for your school.