20 Year 6 Ratio Questions And Answers: From Easy To Hard
Year 6 ratio questions are an important aspect of KS2 maths and pupils must have secure place value, division facts and times tables knowledge to understand ratio.
Here we provide a collection of 20 problem solving ratio and proportion questions that cover the concepts pupils may encounter and can be used as practice questions ahead of the Key Stage 2 SATs.
This article also looks at the key terminology children need to confidently answer Year 6 ratio questions.
How often do ratio questions appear in the KS2 SATs?
Ratio questions appear less frequently in the SATs exams than some of the other national curriculum objectives. However, it is important that children can approach these questions confidently to help prepare them for wider life and deepen their knowledge of ratio in secondary school.
When looking at the SATs questions by topic, in the 2023 papers, ratio and proportion accounted for 7% of all questions across the three maths papers.
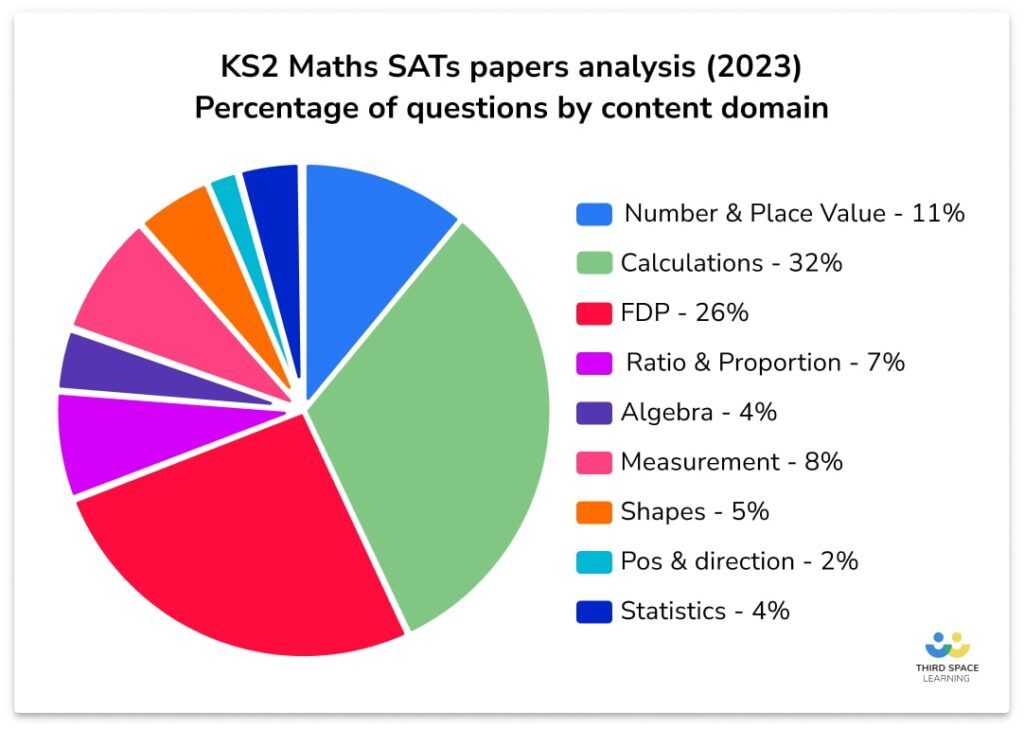
- How often do ratio questions appear in the KS2 SATs?
- 20 Year 6 ratio questions and answers
- Year 6 ratio questions: problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts
- Year 6 ratio questions: problems involving the calculation of percentages and percentages for comparison
- Year 6 ratio questions: problems involving similar shapes where the scale factor is known or can be found
- Year 6 ratio questions: solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
- FAQs
Year 6 ratio questions key terminology
To obtain a secure knowledge of ratio and answer these maths questions in Year 6 securely, children must have a strong understanding of the terminology associated with ratio and proportion.
Key terms Year 6 pupils will need to have an understanding of include:
- Ratio: Explains how much of one thing there is in relation to another thing.
For example, the ratio of boys to girls is 2:3. This means there are 2 boys for every 3 girls.
- Proportion: This explains what the fraction is compared to the whole.
For example, there are 20 pieces of fruit (the whole) and 1 in 4 of those pieces of fruit are bananas (the proportion).
- Equivalent ratios: Ratios can have the same relationship but be written differently.
For example, 1:2 and 2:4 are equivalent ratios.
- Factors: Ths is a number which divides into a number exactly.
For example, 4 is a factor of 12 and 4 divides into 12 exactly 3 times.
- Highest common factor: The highest number that can be divided exactly into 2 or more numbers.
For example, the highest common factor of 12 and 18 is 6. It is the highest number that can be divided into 12 and 18.
- Simplest form: This is the simplest way of showing the ratio. Both both parts of the ratio must be divided by the highest common factor.
For example, 12:18 in its simplest form is 2:3 when both parts are divided by the highest common factor of 12 and 18, which is 6.
- Relative size: How large something is compared to another object.
- Missing value: The quantity or part of the ratio that isn’t initially known or provided. If you only have one part of the ratio, the other part is the missing value.
- Percentage: A ratio expressed out of 100, making it easy to compare things.
For example 75% means 75 out of 100.
- Comparing ratios: Establishing whether one ratio is less than, greater than or equal to another ratio.
For example 1:2 = 2:4 but 1:2 > 1:3
- Comparison of ratio: Comparing the relationship between two or more ratios.
- Scale factor: For 2 similar shapes, the ratio of the corresponding lengths.
- Scaling ratios: Making a ratio bigger or smaller by multiplying or dividing each part by the same number.
- Unequal sharing: Using ratio to share things but not in an equal way.
For example, John gets 2 red sweets for each of Daisy’s 3 green sweets.
200 arithmetic and reasoning questions for Year 6
Download 100 free arithmetic questions and 100 free reasoning questions for Year 6. Includes answers and mark scheme.
Download Free Now!How will these Year 6 ratio word problems help pupils deepen their understanding?
KS2 maths assessments may present ratio questions in different formats:
- Multiple choice
- Short answer questions
- Extended response questions
Exposure to a variety of ratio word problems will help pupils build familiarity with the different types of SATs questions and develop strategies for solving them.
Practising ratio and proportion problems in real-life, relatable contexts helps ensure pupils understand and secure concepts.
Frequent exposure to a range of ratio questions also helps develop pupils’ confidence when faced with them in their Key Stage 2 maths assessments.
This sequence of Year 6 ratio questions becomes progressively harder, enabling pupils to deepen their understanding. Questions may also challenge students who are working at greater depth.
20 Year 6 ratio questions and answers
Year 6 ratio questions: problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts
This first National Curriculum objective requires pupils to compare the 2 sizes or quantities. One value in the comparison may be missing or unknown.
To complete the ratio, children must determine the missing value.
Year 6 ratio question 1
The ratio of red counters to yellow counters is 3:1. There are 12 counters altogether. How many are there of each colour?
Answer: 9 red counters and 3 yellow counters.
3:1 = 4 parts. 4 × 3 = 12
3 × 3 = 9
1 × 3 = 3
Year 6 ratio question 2
Chloe is making a necklace using purple and silver beads in a ratio of 2:1. If she uses 16 purple beads, how many silver beads will she use?
Answer: 8 silver beads
2 × 8 = 16
1 × 8 = 8
Year 6 ratio question 3
Jared is making vegetable soup, using 200g of tomatoes, 120g of onions and 60g of mushrooms. If Jared uses 600g of mushrooms, what weight of onions will he need to use?
Answer: 360g of onions
200 × 3 = 600g
120 × 3 = 360g
Year 6 ratio question 4
If the ratio of green sweets to red sweets in a bag is 2:3. How many of each colour are in a bag of 30 sweets?
Answer: 12 green sweets and 18 red sweets.
2:3 is a total of 5. For a total of 30, we need to work out 2:3 six times.
2 × 6 = 12
3 × 6 = 18
Year 6 ratio question 5
Students in year 6 have chosen their favourite sport. They chose tennis and football in a ratio of 3:5. If there are 80 children in the year group, how many chose football?
Answer: 50 chose football
3:5 = 8 parts.
8 × 10 = 80
3 × 10 = 30
5 × 10 = 50
Year 6 ratio questions: problems involving the calculation of percentages and percentages for comparison
Calculating percentages involves expressing a part of a whole as a percentage.
Children need to be confident applying the concept of percentages to different measures and quantities.
Once pupils have mastered the basic percentage calculations, they can then compare quantities and values and apply their understanding of percentages to interpret pie charts.
Year 6 ratio question 6
Calculate 45% of 740
Answer: 333
10% = 74
40% = 74 × 4 = 296
5% = 37
40% = 296 + 37 = 333
Year 6 ratio question 7
Sam arrives at school at 9am each day and leaves at 3pm. What percentage of the day is he at school?
Answer: 25% of the day.
9 – 3 = 6 hours
\cfrac{6}{24} hours of the day = \cfrac{1}{4} of the day
\cfrac{1}{4} = 25%
Year 6 ratio question 8
In a school, Year 6 has 24 boys and 36 girls. What percentage of the year group are boys?
Answer: 40% are boys
24 + 36 = 60
\cfrac{24}{60} = \cfrac{4}{10} = 40%
Year 6 ratio question 9
Mason wanted to buy a pair of jeans in the sale. The original price was £45 but they were reduced by 15%. How much did he pay?
Answer: £38.35
10% of £45 = £4.50
5% of £45 = £2.25
15% of 45 = 6.75
45 – 6.75 = £38.25
Year 6 ratio question 10
A shop is selling hoodies. One has a full price of £18 but has a 20% discount, the other has a full price of £20 but has a 35% discount. Which hoodie is the cheapest in the sale?
Answer: The second hoodie is cheaper
10% of £18 = £1.80
20% of £18 = £3.60
20% discount = £18 – £3.60 = £14.40
10% of £20 = £2
30% of £20 = £6
5% of £20 = £1
35% of £30 = £7
35% discount = £20 – £7 = £13
Free resource: Year 6 Calculating Ratio Worksheet
Year 6 ratio questions: problems involving similar shapes where the scale factor is known or can be found
Shapes may be considered similar if they have the same shape but not the same size. For example, their corresponding angles are equal and their corresponding sides are proportional.
Here, the scale factor refers to a ratio that describes how much one shape has been scaled, either enlarged or reduced, in relation to another similar shape.
Year 6 pupils need to be able to solve problems related to similar shapes when the scale factor is either known or can be determined if the scale factor can be found.
Year 6 ratio question 11
Oliver says that a scale factor of 4 means the new shape is four times bigger than the original shape. Is Oliver correct? Explain your answer
Answer: No. A scale factor of 4 means each side is multiplied by 4. For example, if a square with sides of 1cm was 4 times bigger, the area would go from 1cm² to 4cm². If each side was 4 times bigger, the square would have an area of 16cm²
Year 6 ratio question 12
Draw a rectangle 4cm × 6cm
Now enlarge the rectangle by a scale factor of 3. What are the new measurements of the rectangle?
Answer: A rectangle drawn with a length of 18cm and width of 12cm
Both sides will be 3 x as long
4cm × 3 = 12cm
6cm × 3 = 18cm
Year 6 ratio question 13
What would the dimensions of a rectangle with a length of 6.5cm and a width of 4.5cm be, if it was enlarged by a scale factor of 3?
Answer: length 19.5cm, width 13.5cm.
Year 6 ratio question 14
Draw a right-angled triangle with a base of 7cm and a height of 3cm.
No enlarge the right-angled triangle by a scale factor of 3.5
Answer: A right-angle triangle with a base of 24.5cm and a height of 10.5cm.
Year 6 ratio question 15
Draw a right-angled triangle with a base of 9cm and a height of 5cm.
Draw a new right-angled triangle using a scale factor of \cfrac{1}{2} .
Answer: A triangle drawn with a base of 4.5cm and height of 2.5cm
More Questions: Year 6 Using Scale Factors Worksheet
Year 6 ratio questions: solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
Pupils must apply their understanding of fractions and multiples to solve problems involving sharing or grouping unequal quantities.
This includes:
- Distributing a quantity among a group of people or containers with different capacities
- Finding the total quantity when given fractional parts of a whole
- Exploring relationships between fractions and multiples when dealing with unequal sharing or grouping situations.
Year 6 ratio question 16
If 600g of tomatoes are needed in a tomato soup recipe for 6 people. How many grams of tomatoes would be needed if there were only 4 people?
Answer: 400g
600 ÷ 6 = 100g
100 × 4 = 400g
Year 6 ratio question 17
A book has 144 pages in total and is split into 6 chapters. How many pages are there in \cfrac{2}{6} of the chapters?
Answer: \cfrac{2}{6} = 48 pages
144 ÷ 6 = 24
2 × 24 = 48
Year 6 ratio question 18
Sam and Amy received £480 between them for Christmas. If Sam received £60 more than Amy, how much did they each receive?
Answer: Sam: £270 Amy: £210
£480 – £60 = £420
£420 ÷ 2 = £210
£210 + £60 = £270
Year 6 ratio question 19
Rosie planted some seeds in the garden. For every 5 seeds she planted, only 3 grew into flowers. If 15 flowers grew, how many seeds did she plant?
Answer: 25 seeds planted
3 × 5 = 15
5 × 5 = 25
Year 6 ratio question 20
A cinema has sold \cfrac{3}{8} of the tickets for the 9pm film. So far they have sold 114 tickets. How many tickets will they have sold if they sell all of them?
Answer: 304 tickets
114 tickets = \cfrac{3}{8}
\cfrac{1}{8} = 114 ÷ 3 = 38
38 × 8 = 304
Free resources for ratio and proportion:
- Year 6 arithmetic questions
- Fraction Questions For Year 6
- Year 6 algebra questions
- Year 6 Introducing Ratio Worksheet
- Year 6 Ratio Independent Recap Worksheet
- 24 Ratio Word Problems for Year 6 to Year 8 With Tips On Supporting Pupils’ Progress
- Ratio Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included
- Ratio – GCSE Maths – Steps, Examples & Worksheet
FAQs
Ratio is how much of one thing there is in relation to something else. For example, for every 2 girls in the class, there are 3 boys. The ratio of girls to boys is 2:3.
Proportion is how much there is of one thing in relation to the whole amount. For example, there are 30 sweets in a bag. 1 in 5 of the sweets are red’.
The four main objectives listed in the National Curriculum are:
• solve problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts
• solve problems involving the calculation of percentages [for example, of measures such as 15% of 360 and the use of percentages for comparison]
• solve problems involving similar shapes where the scale factor is known or can be found
• solve problems involving unequal sharing and grouping using knowledge of fractions and multiples.
There are 40 sweets in a bag. There are 3 red sweets for every 5 orange sweets. How many red and orange sweets are there?
1. Work out the total number of parts.
For example, 3:5 is a total of 8 parts.
2. Find out how much one part is worth, by dividing by the total number of parts.
For example, if there are 40 sweets, split into a ratio of 3:5 red: orange sweets, 1 part would be 40÷8 = 5
3. Multiply each part of the ratio by the value of one part.
For example, red sweets: orange sweets = 3:5
1 part = 5
3 x 5 = 15 red sweets
5 x 5 = 25 orange sweets:
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the SATs revision programme or request a personalised quote from your school to speak to us about your school’s needs and how we can help.




![250+ SATs Questions Free To Download [With Answers]](https://thirdspacelearning.com/wp-content/uploads/2023/12/100-arithmetic-and-reasoning-questions-RL-image-180x160.png)