35 SATs Maths Questions And Answers With Worked Examples: Essential Maths Reasoning Practice For Year 6 [FREE]

For Year 6, the toughest of their SATs maths questions are the reasoning questions. 

No matter how good pupils’ subject knowledge is or how effective your SATs revision lessons are, the examiners always manage to come up with maths questions that can baffle and flummox even the hardiest year 6 pupil.

To mitigate against this for SATs 2024 your pupils need plenty of exam practice and more specifically exam question practice to be familiar with both the types of SATs reasoning questions that can come up and the skills needed to answer them.

So to make life easy for you we’ve put together here a comprehensive collection of 35 SATs maths questions, organised by the sorts of question that pupils can expect to encounter.

All these practice SATs questions have been based on a mix of questions from past SATs papers, our own free year 6 maths SATs papers, and our collections of year 6 reasoning questions from the Rapid Reasoning resource collection. The answers are all taken from the answer sheets we provide for each test paper.

Why the focus on maths reasoning questions for SATs? 

Ever since the new national curriculum Key Stage 2 SATs in 2016, the emphasis in the all SATs papers has been very much on SATs reasoning questions. While there is one arithmetic paper, there are two reasoning papers; and the variety, breadth and level of challenge in the reasoning paper continues to impress us.

Most Year 6 pupils find the reasoning SATs maths questions the hardest part of these maths papers. Unsurprisingly! We teach thousands of pupils every week in the run up to SATs, and teaching them maths reasoning skills at KS2 is a big part of what we do.

We even recently took the decision to restructure our SATs lessons to introduce maths reasoning questions earlier in the learning journey as the level of challenge just at the end of the lesson was too high. So we feel the Year 6 teacher’s pain!

Whatever level pupils go on to perform at in maths, maths reasoning questions and numerical reasoning tests (such as those used by grammar and private schools) are likely to be a part of the practice they require.

35 SATs maths questions for KS2 year 6 SATs

For the KS2 SATs tests, there are 7 types of maths reasoning question that are likely to come up:

1. Single step worded problems
2. Multiple step worded problems
3. Problems involving measures
4. Problems involving drawing
5. Explanation questions
6. Sequence questions
7. Ordering questions

For each of these types we’ll examine an example SATs maths question from a previous SATs paper, looking at the question, the correct answer, and how to go about answering this question.

We’ll also look at further examples of each type of maths reasoning questions and answers from Third Space’s Rapid Reasoning resource, again with worked examples and an explanation of how to answer each.

Finally, at the end of this article we provide links to further Year 6 maths questions, assessments and other SATs papers that you may find useful including plenty of arithmetic practice too.

Our aim is to provide you as part of your SATs practice with a sample of the types of KS2 SATs questions pupils can expect in the reasoning papers and how to teach the reasoning and problem solving skills they’ll need to answer them.

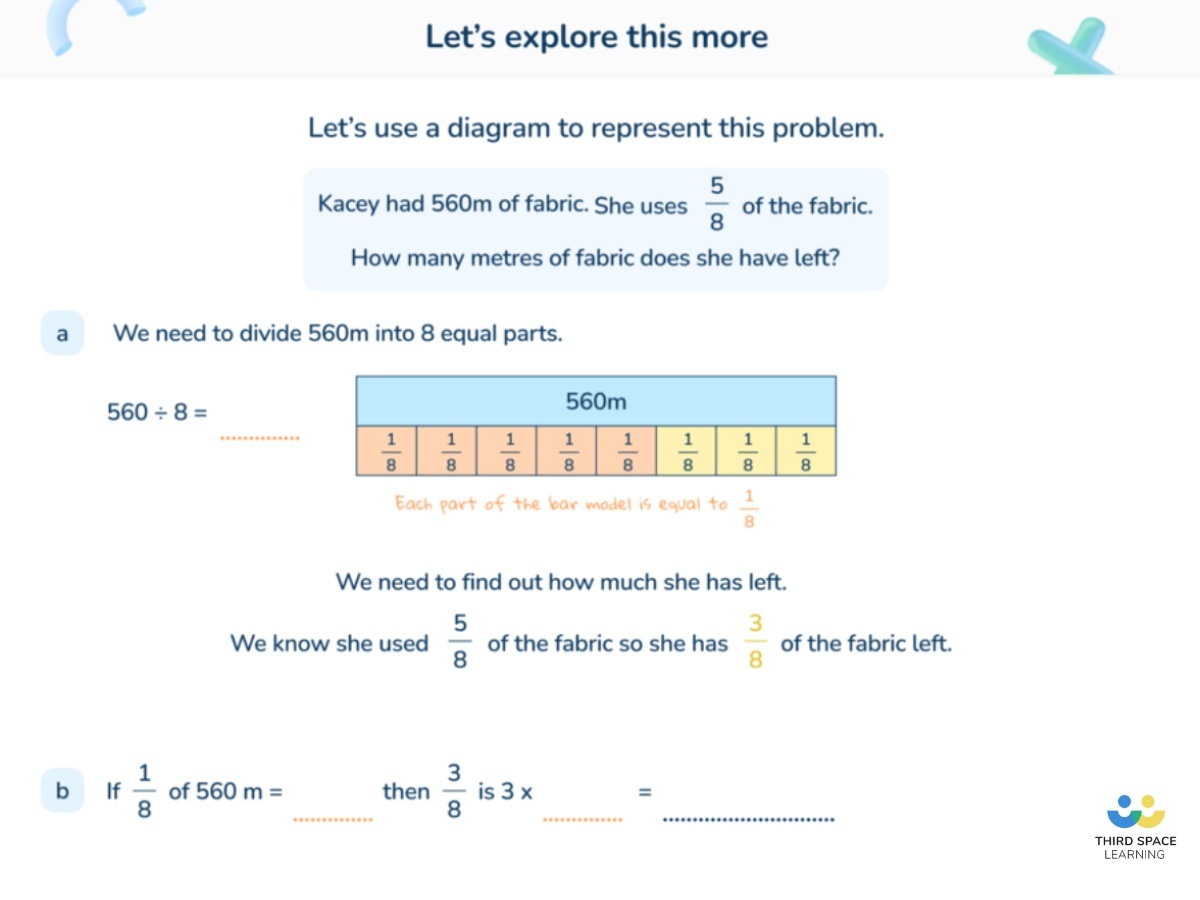
For more word problems like this, check out our collection of 2-step and multi-step word problems for you as well as tips on how to use the bar model to answer Year 6 word problems. For advice on how to teach children to solve problems like this, check out these maths problem solving strategies.

SATs Maths Question Type 1: Single step worded problems

The simplest type of reasoning question pupils are likely to encounter in the reasoning papers, single step problems are exactly that: pupils are asked to interpret a written question and carry out a single mathematical step to solve it.

Have a look at the question below:

Reasoning Question 1

Answer: 65p

A relatively easy question to interpret and solve – the first step is to recognise £2 and £1.35 as equivalent to 200 and 135. From here the simple mathematical step is subtraction i.e. 200-135=65.

The most crucial skill for primary school pupils in this question is a solid understanding of money as relating to place value. If this understanding is present, the mathematical step itself is quite easy.

Below are several more examples, taken from Third Space Learning’s Rapid Reasoning resources:

Reasoning Question 2

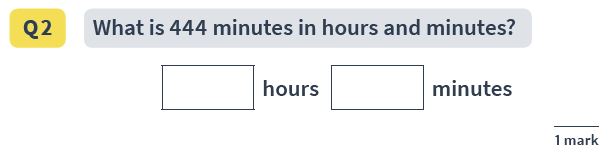
Answer: 7 hours 24 minutes

Pupils need to understand that one hour is equal to 60 minutes. From here the single mathematical step is short division: 444/60, with a remainder.

Reasoning Question 3

Answer: 48 cm³

Pupils must calculate length by breadth by height, using the figures provided by the question.

Reasoning Question 4

Answer: 124 cm

A simple enough calculation (doubling) if pupils are aware that the diameter is twice the radius.

Reasoning Question 5

Answer: 7,590

A single, relatively simple rounding problem – pupils should recognise that ’94’ is the operative part of this figure.

SATs Maths Question Type 2: Multiple step worded problems

A more complex version of the single step worded problem, multi-step problems require pupils to interpret a written problem, but solving it then requires the use of two or three maths skills,

For example, consider this question from the 2019 KS2 maths SATs:

Reasoning Question 6

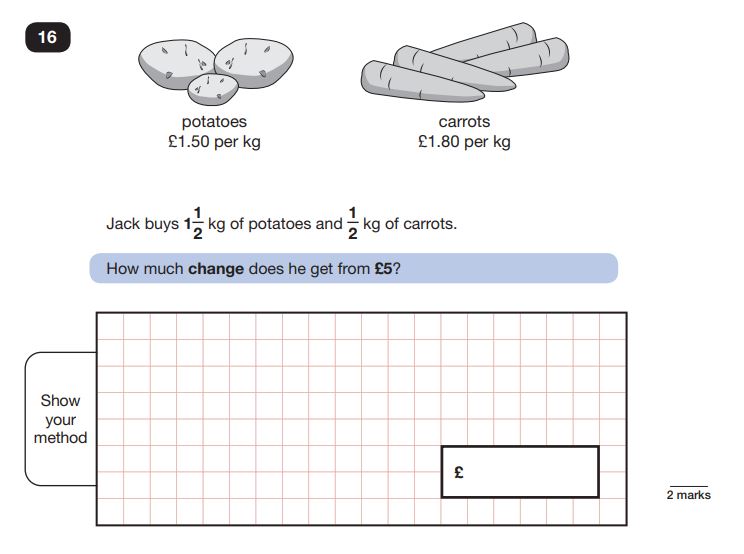
Answer: £1.85

This question encompasses three different maths skills: multiplying (and dividing) mixed numbers, addition and subtraction. Pupils can choose to work out the multiplication or division first, but must complete both before moving on.

Once these values have been worked out the next steps are relatively simple – adding the two values together, and subtracting the total from £5.

Multi-step problems are particularly valuable to include in practice tests because they require children to apply their knowledge of maths language and their reasoning skills several times across the course of a single question, usually in slightly different contexts.

More examples:

Reasoning Question 7

Answer: £5,520

There are two steps to this problem, but both are multiplications. The first is to work out how much money is made per day – 92 x £15. This sum is then multiplied by 4 – the number of days – to get to the solution.

Reasoning Question 8

Answer: 2,160 km

Another two step problem. The first step is to work out 10% of 5400 km. Then multiply this by 4 to solve 40%.

Reasoning Question 9

Answer: £43.50

There are three steps involved in solving this problem: multiplication (doubling £51 and £36 to find the cost of two adult and two child tickets), addition (putting the two costs together) and division (dividing the total by four to obtain the mean cost).

Given the number of steps involved it can be easy for pupils to make arithmetic mistakes, and the mark scheme accounts for this by allowing for one mistake – but no more.

Read more: Mean median mode

Reasoning Question 10

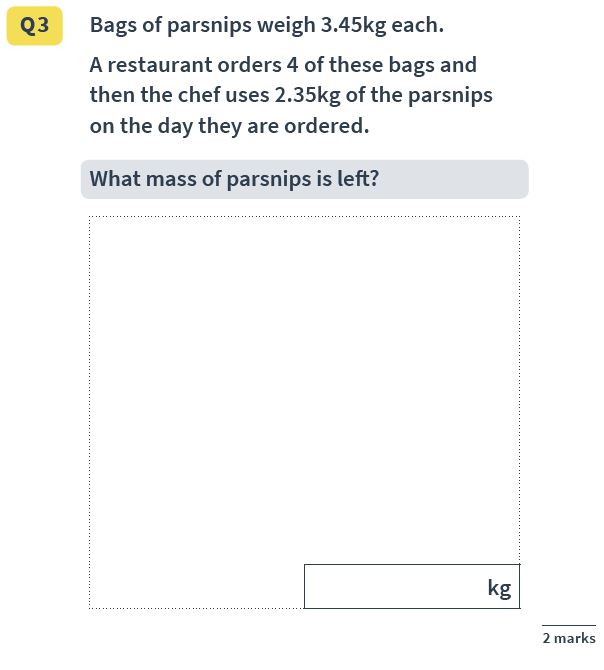
Answer: 11.45 kg

A two-step problem again: multiplying 3.45 kg by 4, then subtracting 2.35 kg from the total. As with the previous problem, the mark scheme again allows for at most one arithmetic error, assuming the method is correct.

SATs Maths Question Type 3: Problems involving measures

As their name suggests, these questions ask pupils to solve a problem that includes one or more units of measurement.

Take a look at this question from 2018’s Reasoning Paper 3:

Reasoning Question 11

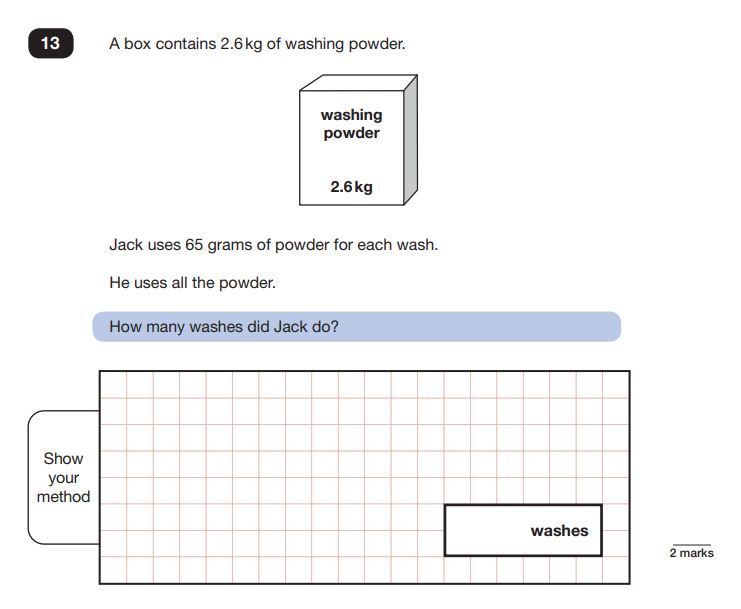
Answer: 40 washes

This is a two step problem; pupils must first be able to read and convert kilograms to grams (and therefore know the relationship between the two units), then divide 2600 by 65 to work out the number of washes possible.

Questions involving measures tend to be few in number in the KS2 exam papers, but they often provide an excellent way to couch key maths skills such as the four operations.

Further examples:

Reasoning Question 12

Answer: 50g

A relatively simple division problem, relying on pupils having knowledge that 200g is one fifth of a kilogram.

Reasoning Question 13

Answer: 1.1kg

Another three step problem – multiplying 500 by 4 to get the total mass of the four melons, multiplying 300 by 3 to get the total mass of the remaining three melons, and then subtracting 2000 from 900 to obtain the mass of the fourth melon.

It’s worth noting that the mark scheme allows either 1.1kg or 1,100g as acceptable answers – the units of measurement are not as important as obtaining the current figure.

Reasoning Question 14

Answer: 216cm

Interesting to note that in this problem (unlike the previous example), the units for the answer are specified – an answer given in metres will be marked as wrong, since cm is specified in the answer box. This is why we encourage pupils to keep an eye on whether units are provided in the answer box.

Reasoning Question 15

Answer: 170g

As with the melon question there are three steps involved to solve this problem: working out the mass of the four cars (4 x 80), working out the mass of the remaining three cars (3 x 50) and subtracting 150 from 320 to get the mass of the fourth car.

SATs Maths Question Type 4: Problems involving drawing

Problems involving drawing require pupils to construct an accurate drawing by following a set of instructions, or through reflection, translation, or scaling.  

This type of question is quite rare, but there are some notable exceptions, such as the infamous Question 21 in Paper 2 of the 2019 Reasoning SATs:

Reasoning Question 16

Answer: Any pair of lines that make a square of 4 units, a rectangle of 6 units, and a square of 25 units.

This question is considerably more complex than it appears, and incorporates aspects of multiplication as well as spatial awareness. One potential solution is to work out the area of the card (35), then work out the possible square numbers that will fit in (understanding that square numbers produce a square when drawn out as on a grid), and which then leave a single rectangle behind.

A lot of work for a single mark!

Some further examples:

Reasoning Question 17

Answer: Any quadrilateral made by joining the dots that has 3 acute angles e.g. an arrowhead shape.

Reasoning Question 18

Answer: An accurately drawn angle.

The mark scheme here allows some room for error – “between 34 and 36 degrees” is acceptable .

Reasoning Question 19

Answer: An accurately drawn angle.

As with the question above, a small amount of room for error is given – “between 139 and 141 degrees”.

Reasoning Question 20

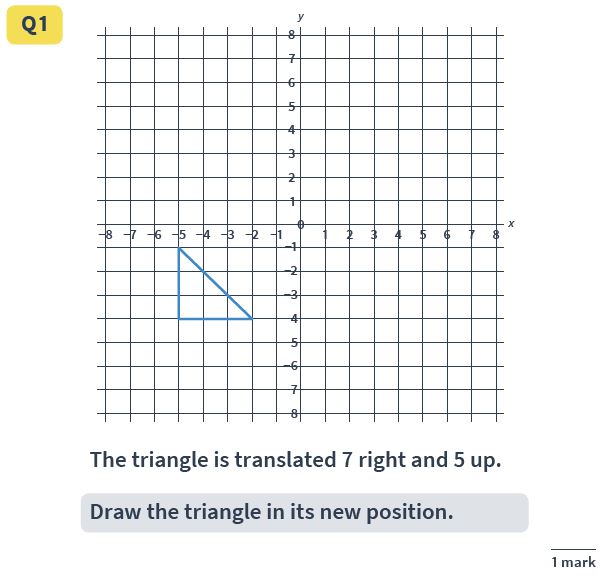
Answer: a new triangle drawn with points at (2,1), (5,1) and (2,4).

Translation can be tricky for pupils. Encourage them to look at the triangle as three points, and to translate each point separately rather than trying to move ‘the whole triangle’.

SATs Maths Question Type 5: Explanation questions

An early form of the ‘Prove X’ questions that come up in GCSEs, these problems ask children to explain a mathematical statement or error.

As an example:

Reasoning Question 21

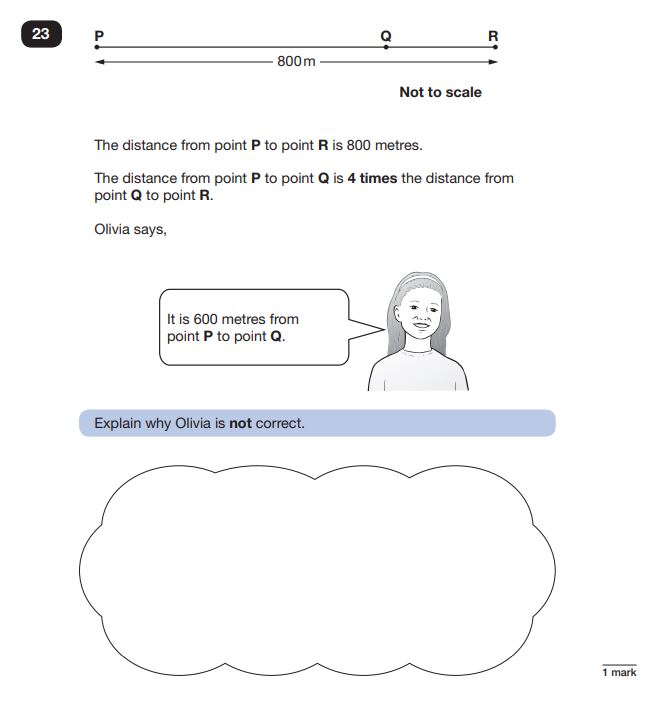
Answer: If the distance from P to R is 800m and the distance from P to Q is (Q -> R x 4), it must be 4/5 of 800 = 640m. Therefore Olivia is wrong.

More than most problems, this type requires pupils to actively demonstrate their reasoning skills as well as their mathematical ones. Here pupils must articulate either in words or (where possible) numerically that they understand that Q to R is 1/5 of the total, that therefore P to Q is 4/5 of the total distance, and then calculate what this is via division and multiplication.

Further examples from TSL’s Rapid Reasoning resources:

Reasoning Question 22

Answer: No; 20/100 is the same as 20 divided by 100, which equals 0.2.

Reasoning Question 23

Answer: No; multiplication and division have the same priority, so in a problem like 40 x 6 ÷2, you would carry out the multiplication first as it occurs first.

The mark scheme notes that vague answers or any answers with a mathematical error are unacceptable.

Reasoning Question 24

Answer: No

Any explanation that provides a counter-example is acceptable e.g. “Not if the number is 1”, “Not for 0” etc.

Reasoning Question 25

Answer: Any answer that refers to the fact that there is a 5 in the hundreds place, AND a 9 in the thousands place, so that the number has to be rounded up as far as the ten-thousands place.

SATs Maths Question Type 6: Sequence questions

Another relatively simple kind of reasoning question, sequence problems involve pupils completing mathematical sequences.

Consider this example:

Reasoning Question 26

Answer: 35, 42, 49, 56, 63, 70

Number sequence questions, particularly those that involve linear sequences or (as in this case) times tables, come up relatively frequently in the SATs maths tests. The question’s instructions point clearly to the solution: work out what the increase between numbers is, then apply this via addition or subtraction to find the missing numbers.

Higher attaining pupils might quickly pick up that this is in fact the 7 times table and rely on their knowledge of multiplication facts to obtain the answer – this should be encouraged so long as they then check their answer in the normal method to ensure they haven’t made a mistake.

More examples:

Reasoning Question 27

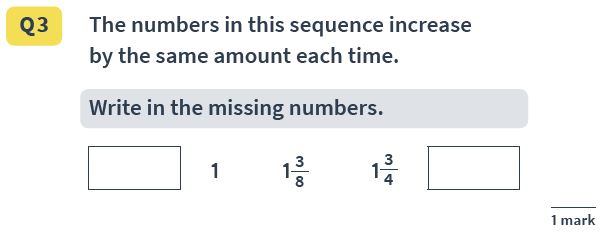
Answer(s): 5/8 and 2 1/8 (OR 17/8)

Both answers must be correct to receive the mark. Pupils must recognise that 3/4 is the same as 6/8, so the following number must be three eighths higher.

Reasoning Question 28

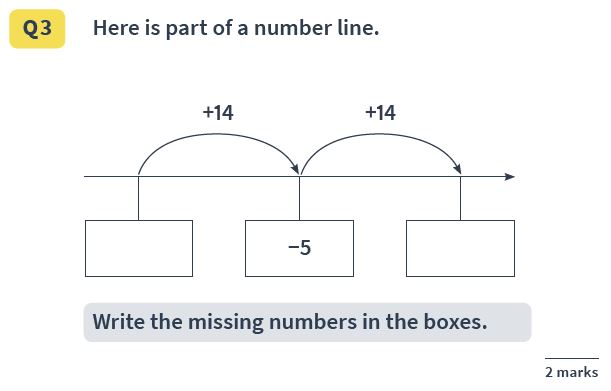
Answer(s): -19 and 9

Reasoning Question 29

Answer(s): 128, 135 and 156.

Reasoning Question 30

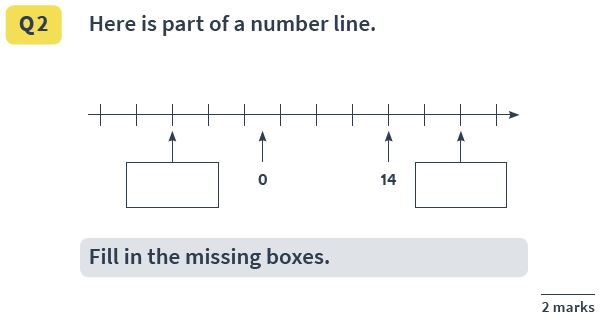
Answer(s): -10 and 22

This question can be a little tricky; pupils need to work out that the marks on the line represent increments of 4, and count backwards and forwards in 4s to obtain the missing numbers.

SATs Maths Question Type 7: Ordering questions

A slightly more complex variation of the sequence question, ordering problems require pupils to put a set of numbers, fractions or measures in the correct order.

A good example is this question from Paper 2 of the 2018 SATs:

Reasoning Question 31

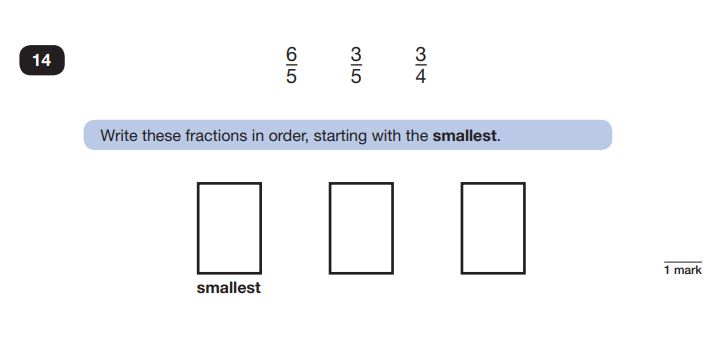
Answer: 3/5, 3/4, 6/5

This question throws a stick in the wheels by including an improper fraction, but this is hardly unusual. These sorts of questions are just the place to find other ‘curveballs’ such as equivalent fractions, mixed numbers and decimals and fractions combined.

A good knowledge of the fundamentals of fractions is essential here: pupils must understand what a larger denominator means, and the significance of a fraction with a numerator greater than its denominator.

Further examples:

Reasoning Question 32

Answer: D,C,A,B

Encourage pupils to convert all the fractions to one denominator value to make ordering easier.

Reasoning Question 33

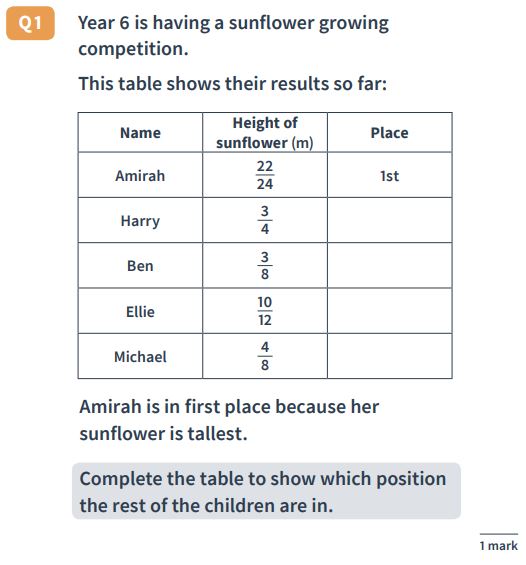
Answer: (descending down the ‘Place’ column) 3rd, 5th, 2nd, 4th

As with the example above, pupils should be encouraged to convert the fractions to make it easier to order them.

Reasoning Question 34

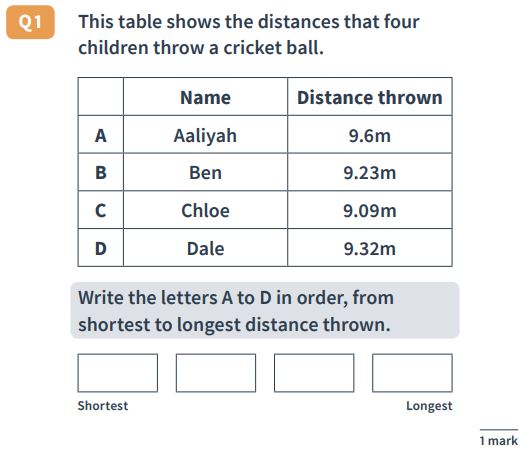
Answer: C, B, D, A

Reasoning Question 35

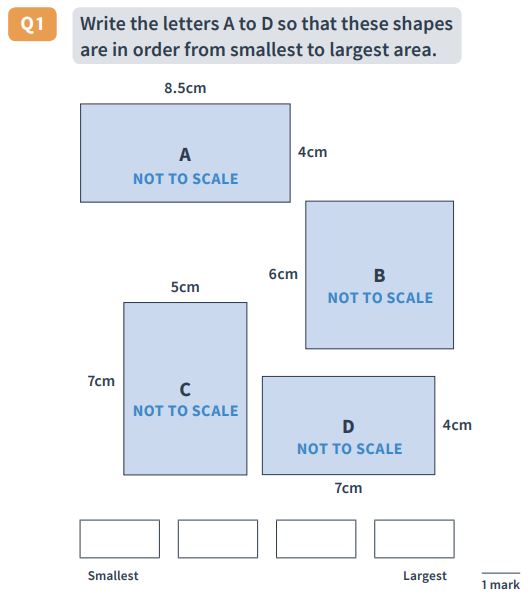
Answer: D, A, C, B

7 top tips for answering SATs questions

Now that we’ve covered how to answer some specific types of reasoning questions, here are some more generic tips for success in the reasoning papers. They may not all be applicable to every single question type, but will apply to at least two, usually more.

• Get pupils in the habit for any practice paper of identifying what information they’re given in a question, and what they need to know to solve the problem. This helps them start to form the steps needed to find the solution.
• Ask pupils to ‘spot the maths’ in a question – which calculations or skills do they actually need to use to solve the problem? This is useful even for arithmetic questions – it’s no surprise how often children can misread a question.
• Check the units! Especially in questions involving multiple measures, it can be easy to give the answer in the wrong one. The answer box might give a specific unit of measurement, so pupils should work to give their answer in that unit.
• In a similar vein, remind pupils to convert different units of measurement in a question into the same unit to make calculations easier e.g. kg to g.
• Encourage numerical answers where possible. Even in explanation questions demonstrating the mathematical calculation is a better explanation than trying to write it out.
• The bar model can be a useful way of visualising many different types of questions, and might make it easier to spot the ‘steps’ needed for the solution.
• Check your working out! Even if the working is ultimately irrelevant to the question, you can lose marks if it is wrong.

Online 1-to-1 maths lessons trusted by schools and teachers
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress. Since 2013 we’ve helped over 80,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote to speak to us about your school’s needs and how we can help.