How To Help Primary School Pupils Develop The Maths Language Skills They Need To Succeed In SATs

Maths language is an aspect of maths teaching we may not often consciously consider when planning and delivering lessons, because we’ve already been through the process of absorbing and becoming fluent in it. 

But explicit teaching of mathematical language is one of the most important and impactful aspects of developing our pupils into able mathematicians.

With that in mind, let’s take a detailed look into why maths language is important, how it might be presented, and how we can teach it effectively.

Looking for a particular part of this post? Follow the links below:

• What Is Mathematical Language?
  • 8 Dimensions of Maths Language Found In The SATs
• Why Is Mathematical Language Important?
• Mathematical Language In The SATs
• What Can SATs Papers Tell Us About Maths Language?
• 7 Strategies For Teaching Maths Language Effectively At KS2

What Is Mathematical Language?

Before we can define mathematical language, we must first consider what we believe the function of language itself to be. Language is defined as, “the method of human communication, either spoken or written, consisting of the use of words in a structured way”.

So, mathematical language is the means through which children can communicate meaning and ensure it is presented in a structured way. Whether written or spoken, we want children to be able to present their thinking and reasoning through the use of maths vocabulary. After all, if you are to be fluent in a language, you must be able to both think and speak in it.

Moreover, the mathematics National Curriculum explicitly states that we must teach children to “reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language”.

Through doing this, children can construct their own understanding and add to their existing schemas of knowledge. If we teach vocabulary instruction explicitly and place an expectation on children to reciprocate, it will deepen their understanding of the content we teach.

How Does Maths Language Differ From ‘Normal’ Written Or Spoken Language?

If we are to view language as the communication of meaning, mathematical language differs significantly, because it extends to include the use of graphs, charts, mathematical symbols, diagrams and numbers. This variation in the representation of language can make it more difficult for children to construct meaning. It is evident that maths, as a language, has a rather unique phraseology and vocabulary.

Our goal is for children to understand the disciplinary literacy of mathematics, so that they can become truly mathematically literate. It is this understanding of mathematical language where children often falter during the SATs reasoning papers. This is especially true of the last few questions on either reasoning paper.

8 Dimensions Of Mathematical Language Found In The SATs Reasoning Papers

This is, however, understandable, as mathematical language can be complex and confusing. Below are eight dimensions of maths language I have identified that children encounter in the reasoning SATs papers:

1. The breadth of synonyms linked to one of the four calculation types (take instead of subtract, product instead of answer, altogether rather than add)
2. An understanding of superlatives (biggest, largest, tallest, smallest)
3. Words that can have different meanings outside of a mathematical context (round, product, factor, prime)
4. Terms other than superlatives that suggest comparison (between, more/less than, each, share, in order, sorting, put in the correct place)
5. Their understanding of the difference between the right answer and the wrong answer (best estimate, explain why Jack is not correct, write the correct symbol in each box, circle the improper fraction that is equivalent)
6. Verbs implying mathematical meaning (remaining, left, combine, collect, spend)
7. Compression of vocabulary through nominalisation and noun phrases – prime number, improper fraction, roman numeral, perpendicular and parallel lines, 3D shape
8. Abstract nouns – circumference, multiplication, area, perimeter

Why Is Mathematical Language Important?

Language is not learnt incidentally, nor through limited and infrequent exposure. Teaching vocabulary in this way leads to a superficial level of understanding and prevents the mathematical proficiency we want our students to develop. A child cannot pursue mastery of a mathematics topic without understanding the vocabulary associated with it. It is this vocabulary that truly enables children to engage with concepts and build a deep understanding of them.

By ignoring explicit vocabulary instruction and the understanding it affords, we are preventing children from achieving the depth of knowledge we want them to achieve. How can a child reason out word problems or justify their arguments, if they cannot think in the language that we are asking them to communicate in?

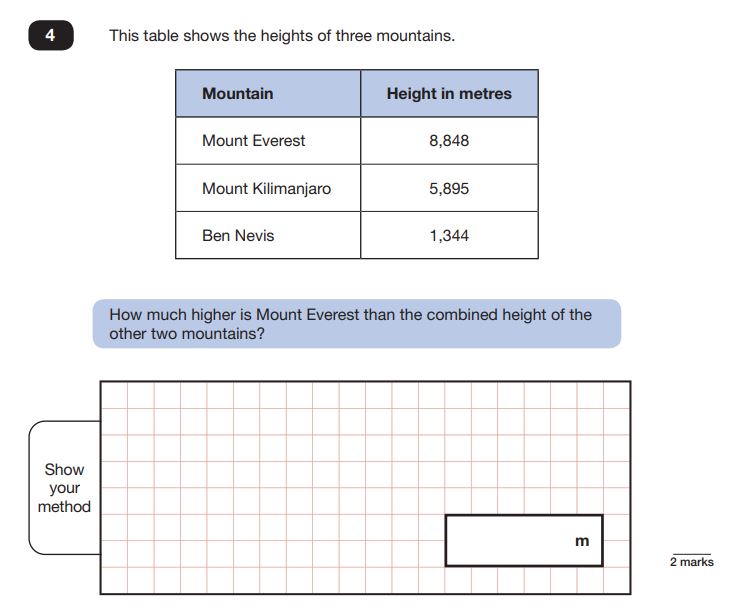
Realising that even the most proficient mathematics students could struggle with vocabulary sparked my initial interest in vocabulary instruction. While watching my class undertake a SATs reasoning paper in 2017, one of my most knowledgeable mathematicians put up his hand. He looked at the question below and asked me what ‘combine’ meant.

Difficulties Caused By Overlooking Maths Language Teaching

Naturally, I was unable to tell him, but he had enough understanding to make an educated guess, because he could gather information from ‘how much higher’. What about his peers who were less knowledgeable of mathematical language? I can recall that more than one chose to subtract rather than add. This is only the fourth question of the paper I may add, where cognitive load was significantly less intense than the questions at the other end of the paper.

Read more: Cognitive load theory in the classroom

This was my first year in Year 6 and only my second year of teaching. I had not even heard of explicit vocabulary instruction at this point in my career. This seems to be a common issue, as explicit vocabulary instruction is often overlooked in a maths classroom (Adams, 2003; Riccomini and Witzel, 2010).

When we overlook language, we relinquish the opportunity to activate prior knowledge, to revise content already learnt, for children to construct meaning and the chance to consolidate important language to long-term memory.

And while language may be ever-present in some maths classrooms, it is often only a surface-level exposure. Some teachers may only display keywords on their working walls; others may misunderstand a mastery approach and rush children through content to get them to a problem-solving stage quicker.

(If you’re interested in finding out more about the most beneficial method of introducing children to solving more complex problems, you can ready Third Space’s Ultimate Guide To Problem Solving.)

Either way, vocabulary instruction is insufficient and the maths classroom is being robbed of the vestiges of mathematical language. Too often we are tasking children with problem solving without having the language foundations to attempt questions independently and successfully. A realisation I came to too late in 2017 for my year 6 class.

Teachers have tried to reduce the complexity of mathematical language by getting children to circle keywords, discuss with partners who have a lack of understanding or by using RUCSAC (Read, Underline, Choose, Solve, Answer and Check). These methods are trying to oversimplify a complex process. Mathematical language is not this straightforward.

---

How Third Space Learning embeds maths language teaching into 1-to-1 online interventions

Helping pupils become mathematically fluent is a key part of Third Space’s philosophy, and effective teaching of mathematical language is woven into every part of the 7000 online, 1-to-1 interventions delivered to pupils across the UK every week.

Important vocabulary is highlighted by tutors in their session notes, which they can then use in lessons to help pupils identify and make sense of the topic(s) they are studying. Tutors are also given regular CPD sessions to ensure their own command of the ‘maths language’ stays topped up.

The intervention lessons themselves reinforce the vocabulary being learnt by repeating it through several layers of context so that pupils gain an understanding of both the words and the ways in which they may be used as part of a problem – which in turn makes it more likely that they will retain and fully understand what they have learnt.

To find out more about how Third Space Learning’s online 1-to-1 interventions could help your pupils become more fluent mathematicians, call 0203 771 0095 or book a demo today.

---

Mathematical Language Must Be Explored To Be Absorbed

Simply exposing children to maths language is insufficient. We must first understand the difficulties that language presents, before we can begin to counteract them and therefore teach children how to interpret more successfully. It is because of this that the three methods mentioned above are ineffectual and not fit for purpose.

Moreover, if meaning is only ever presented by the teacher and negotiated, then children will never consciously construct meaning for themselves. Meaning is derived from the context within which it manifests. Therefore, it is the teacher’s duty to frame the dialogue for such meaning to occur. We must think carefully about the language we use during our inputs and to construct questioning, as well as the pictorial representations that accompany this language.

When we do not explore language through a range of pictorial and abstract representations, children do not form a depth of mental representation. A child’s visualisation often ends up as just a representation of the concrete. The Mastery Maths approach is not achievable if visual representation is one dimensional – language must be embraced and explored throughout the thought process, whether through the concrete, pictorial, abstract approach or another similar method.

Try asking a large group of pupils to draw a rectangle. While the vast majority may draw it horizontally, very few, if any, will draw a square. Children tend to believe that a rectangle has two long sides, two short sides and is always represented as horizontal. Read more on maths terminology here.

As a SATs marker, I have noticed certain questions have caused children issues. In last year’s tests, this was particularly true of the question below.

In just over 1,000 instances of this question that I marked, I saw the word ‘composite’ in an answer just once. While this was not a necessity to achieve the mark, I thought it to be indicative of an overarching issue – vocabulary is not taught effectively enough or in enough depth.

Additionally, a huge proportion of children answered this question incorrectly by stating that ’95 goes into 5 and 87 goes into 3’. These children have understood what a prime number is, that 89 is indeed the prime number out of the given choices and still they have received 0 marks because of their disarticulation.

While we can all decipher what the children really meant, mathematically, their statement is far from correct. There is no leniency provided in either the SATs papers or the National Curriculum in general to incorrect interpretations of language and nor should there be.

This was also true of children who discovered that 95 and 87 were not prime but claimed that 89 was prime, because it ‘can’t be divided by a whole number’ or ‘no numbers go into 89’. We can gather these children loosely understand the concept of a prime number, but they lacked a depth of understanding that will gain them the mark.

Mathematical Language In The SATs

Alex Quigley from the Education Endowment Foundation posits that, “Vocabulary is a proxy for your background knowledge”. I agree with this statement and think it is particularly applicable to the SATs reasoning papers. The more vocabulary a child knows from a topic, the more knowledge around that topic they have.

Below is a table showing the maths vocabulary or phrases that have appeared in every reasoning paper since the sample papers were released in July 2015. The amount and variation of language used demonstrates the depth of knowledge children are required to access the SATs papers each and every year.

SATs paper by year	Mathematical terms mentioned throughout the paper
2015 Sample	Paper 2 – More than, how many left, each take, difference between, warmer than, equivalent fraction, square, hours and minutes, minutes fast, correct time, multiple, circle, numbers from, formula, cost, calculate, show your method, triangle, measure, shortest, accurately, centimetres, largest, angle, missing digits, long multiplication, numerals, figures, halfway between, octagon, vertices, parallel, perpendicular, round, nearest, isosceles, rectangle, together, share equally, how much each, mean, height, pie chart, one gram, half a kilogram   Paper 3 – sorting, diagram, multiple, number line, missing numbers, digit, hundreds place, hundredths place, collect/collected, more than, each month, altogether, amount of money, millilitres, measuring, level, ml, complete, translated, new position, mass, half, altogether, costs, how much more than, missing digits, addition, correct, decimal numbers, equal, add together, other number, fraction, number pyramid, product, below, quadrilateral, acute angles, less than, divides, subtracts, result, answer, started with, cubes, percentage, how much, only, area, square metres, metres long and wide, how much larger, identical, coordinates, axes
2016	Paper 2 – number line, closest, furthest, lowest, in order, price, missing digits, addition, correct, table, total, difference, prime numbers, even numbers, square numbers, squares, reflection, equivalent fractions, correct, add together, equal, cost, divided, sections, three-quarters, how many days does it last, value, identical, cm, tall, takes, all, common multiples, less than, million, hundred thousand, angles, calculate, triangles, coordinate axes, vertices, axis, vertex   Paper 3 – sequence, increase, each time, missing numbers, difference, table, lower than, digital clocks, twice, stands for a number, total, value, each shape, in order, smallest, metres, pieces, length, angles, obtuse, acute, change, cost, timetable, how many, to reach, earliest, cuboid, different, volume, each box contains, total, translated, position, triangle, squares, right, down, divides, adds, result, answer, started with, each sentence, seconds, hour, minutes, day, nearest hundred, rounding, mass, small, large, same area, different area, diagonals, quadrilateral, cross, right angles, multiply, together, equal, 1 million, spent, three-quarters, money left, start with, answer
2017	Paper 2 – graph, results, altogether, how many, how many more, 10 times, greater than, missing numbers, multiplication grid, how much higher, combined, 1,000 more, smallest, order of size, months, hours, days, years, weeks, delivered, sold, how many left, 3/4, round, nearest, plus, extra, kilogram, minutes, mass, 3D, faces, vertices, cube, square-based pyramid, triangular prism, triangular-based pyramid, how much more, pay, for every, numerals, figures, one-and-a-half, degrees, quadrilateral, coordinates, percentage, each day, costs the same, change, smaller than, correct, represents, kilometres, distance between, similar, right-angled, triangles, ratio, circle, fraction, whole circle,   Paper 3 – missing number, division, correct, equally, share, each, digit, multiplies, together, 2-digit, 1-digit, multiple, multiplication, warmer, lower than, target, to reach, arrive by, latest time, leaves, arrives, triangle, coordinate, grid, translated, right, up, position, factors, timetable, total, hours, am, pm, millilitres, half a litre, how much is left, diameter, radius, four times as many, pentagon, acute angles, exactly, costs the same as, parallel, perpendicular, share equally, greater, square number, prime number, total, whole number, rounds, nearest, answer, possible numbers, square, longer, narrower, difference, area, between, sequence, increase, same amount, each time, equal width, pattern, number pairs, rule, same volume, cuboid, missing length
2018	Paper 2 – symmetrical, mirror line, grid, shape, design, calculation, addition, answer, centimetres, equivalent fractions, missing values, temperature, midnight, midday, degrees, colder, sequence, decrease, same amount, each time, next, equivalent, large, small, altogether, how many, every four years, correct symbol, statements, correct, 3D shape, faces, vertices, edges, translated, moves, position, improper fraction, fractions, smallest, mental method, add, subtract, litres, millilitres, left over, cost, mean, estimate, best estimate, length, estimated, measuring, distance, multiplying, difference, different, value, net, cube, volume, times   Paper 3 – sequence, increase, same amount, each time, missing numbers, missing combinations, four-digit, tens column, higher value, other digits, remaining two digits, addition, missing digits, correct, common factors, both, chart, altogether, different, statement, true, more than, total number, one-quarter, each box, holds, how many, fill, left over, has, spend, metres, tall, wide, scale model, centimetres, square, coordinate grid, vertices, marked, missing vertex, millilitres, measuring, tale, areas, larger, times, contains, grams, kg, angles, triangle, equilateral, not correct, formula, price, how many left, opposite, faces, draw, net, fractions, remaining area, multiplication, each day, altogether, greatest, after, take, before
2019	Paper 2 – multiplications, three, missing, number, less than, largest, smallest, shape, square, grid, reflect, mirror line, sequence, increase, each, division, litres, multiply, add, multiplied, added, answer, calculate, total, cost, pounds, one, one-quarter, kilogram, scales, decimal, how much, change, symbols, correct, triangle, accurately, angle measurer, protractor, nearest, round, percentage, two, same, perimeter, regular, hexagon, length, area, circle, prime number, millilitres, every, 4, seconds, minute, fractions, equal, rectangular, straight, divide, different, maximum, temperature, five, days, below, mean, one decimal place, cuboid, centimetre, cubes, longer, taller, wider, difference   Paper 3 – original, price, off, sale, digit, ten thousands, place, round, nearest million, how much left, expression, amount, money, one, masses, lightest, kg, missing, digits, addition, correct, change, difference, heaviest, lightest, number, another, more, pictogram, three, grid, plots, quadrilateral, translates, squares, right, position, five, each, prime numbers, factors, cm, length, width, one-tenth, scale model, double, acute, angle, obtuse, not correct, days, September, October, November, altogether, height, miles, kilometres, equals, km, whole numbers, less than, x, y, fractions, how many, altogether, complete, rectangle, coordinate axes, sides, parallel, not to scale, centre, coordinates, six, identical, right-angled, triangles, calculate, distance, 4 times, metres

A child did not necessarily need to understand every single one of these words to be able to comprehend and answer all the questions, but the table is indicative of simply how many words children are expected to know in their pursuit of 70 marks across the two papers.

When a word appeared more than once in a single paper, it was omitted from the table. This is important to consider, because if a child does not understand what a ‘rectangle’ is when it first appears, they are not likely to understand it when it appears again further on in the same paper. It is also important to remember the mathematical symbols that the table also omits, like £ and %.

What is clear from the table above is that we cannot, as teachers, rely so heavily on everyday language during our inputs and modelling. We must look to use maths language – and maths language that is specific to the topic being studied. This is what Beck et al (2013) refer to as ‘tier three’ vocabulary, more commonly known as subject-specific vocabulary.

‘We take from here and put it there’ is not as effective as we ‘transfer from the hundreds column into the tens column’. The former is not context specific and could be used across more than one place value column. The latter serves to cement understanding more clearly and adds to the child’s pre-existing schema of knowledge.

Moreover, as we think about the children we teach transitioning to secondary school, can we be sure that the everyday language we rely on will be heard in the maths classrooms they will enter in year 7? Will our colloquialisms pervade? Not every teacher will say ‘borrow’ and nor should they!

Keywords and mathematical language, however, will surely be a mainstay of their future classrooms. It is the one way we can guarantee consistency in how maths is taught across primary and secondary. While pedagogies and methods may differ, subject-specific terminology cannot.

You can download Third Space Learning’s Ultimate Maths Vocabulary List and an Ultimate Maths Vocabulary Activity Guide that accompanies it for free!

What Can SATs Papers Tell Us About Maths Language?

The language used in the maths reasoning papers gives children a lot of information that they can use to help them unpick and interpret questions successfully. For example, if they understand that the term ‘change’ (money), always means a subtraction must be performed (i.e. amount given – cost), they are more likely to interpret a question that includes that term.

By teaching children to recognise such a term, we can begin to free up their working memory by getting them to access information stored in their long-term memory instead. In doing so, this can perhaps allow them to interpret two-step questions more readily, as they understand the term ‘change’ implies a subtraction as the final step. This allows them to focus on the first step instead.

Perhaps the most important language information children can understand for the tests is the synonyms or terms used that indicate a specific operation is required.

Terms Used to Indicate The Four Operations

Operation	Synonyms and short phrases used in the 2015, 2016, 2017, 2018 and 2019 tests to indicate these operations
Addition	More than, twelve minutes fast, mean, altogether, add, together, total, increase, adds, combined, more, plus, add, and, sum, after, another
Subtraction	How many left, difference, how much more, subtracts, how much larger, difference between, takes, less than, lower than, change, how many more, how much higher, how many warmer, pours out, how many colder, decrease, different, before, off
Multiplication	Multiple, long multiplication, product, total, area, multiply, times, each, for every, ratio of, multiplies, factors, together, three-quarters, times larger, scale
Division	Halfway, share equally, mean, half, divides, each, divided into equal sections, factors, multiple, how much is one or how much does one cost, one-quarter, three-quarters, scale, times larger

NB: All the words in bold above have suggested different operations in different questions, or that one of two operations could be used to solve one specific question.

We can therefore teach children that certain terms have very specific connotations. For example, ‘difference’ has always indicated a subtraction and the term ‘altogether’ has always indicated an addition.

As shown by the words in bold above, some terms can be applied to more than one operation – e.g. ‘scale’. This is an important teaching moment, as this can often mean a link between inverse operations (but not always – see ‘total’ above). Children should be made aware that terms like ‘scale’ may mean a division or multiplication based on the context in which the word finds itself. They should see such a term in a variety of contexts so that they do not solely rely on the definition of the term itself.

If children are aware of the definitions, as well as the implications, of mathematical vocabulary, then they can begin developing reasoning skills more effectively. Language, after all, is about an understanding of both breadth and precision.

Frequently Occurring Terms

Children should also be made aware of the most frequently occurring terms and the connotations they have. There are many terms that have occurred frequently over the past 5 years (including the sample papers released in July 2015).

Most frequently occurring terms	Frequency
2015	2016	2017	2018	2019	Total
Correct (sometimes as ‘not correct’)	5	4	4	6	7	26
‘Equivalent’ or ‘equal’ or ‘equally’	3	4	2	4	2	15
‘Missing’ (as in digit, number etc)	2	4	7	5	8	26
‘Cost’ and ‘costs’ and ‘price’	10	10	5	6	5	36
Each	10	12	11	13	10	56
‘Total’ and ‘altogether’ and ‘together’	4	7	5	3	4	23
‘How many’ and ‘how much’	11	4	14	11	11	51

When terms like the ones above appear so frequently, it underpins how important explicit vocabulary instruction is. If we were to explain to children that whenever ‘how many left’ has appeared, it has always indicated that a subtraction was required, this can make them more successful in interpreting questions and answering them correctly.

Frequently occurring comparative terms	Frequency
2015	2016	2017	2018	2019	Total
‘Difference’ or ‘different’	1	4	1	3	3	12
‘Than’	8	5	8	6	4	31
‘Less’ and ‘more’	3	4	5	2	4	18
Nearest	3	2	4		4	13

Comparative terms are also of significance. They always appear in the reasoning papers and can help children to interpret the questions more easily. For example, I noticed this question could have been solved more efficiently if children had a better understanding of the language used.

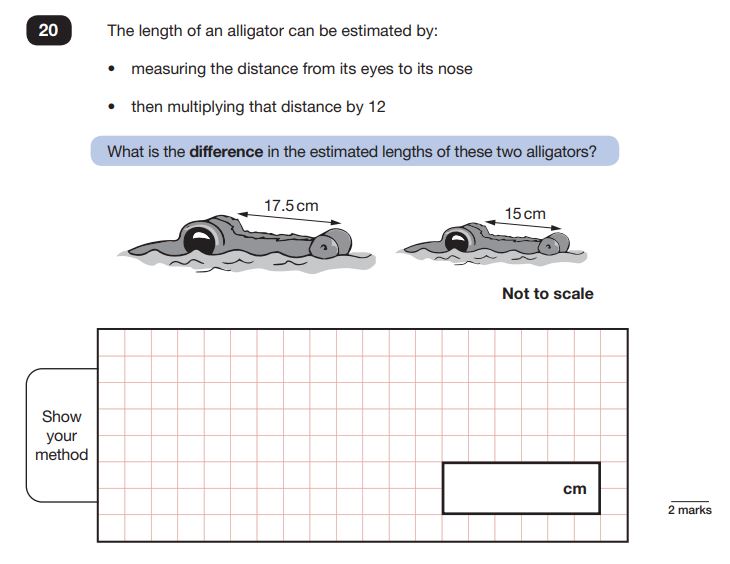
Most children were misled by the two bullet points, deciding that they needed to multiply 17.5 by 12, then multiply 15 by 12 and finally find the difference afterwards. Had children focused on what the term ‘difference’ really means, they could have realised that they could have subtracted 15 from 17.5 and then simply multiplied their answer by 12.

Naturally, you can see why children can often struggle with the later questions in a reasoning paper, such as the alligator one above. Their understanding of the language of mathematics is not strong enough to allow them to interpret effectively.

Comparative and Superlative Terms

Comparative and Superlative terms	Frequency
2015	2016	2017	2018	2019	Total
Warmer	1		1			2
Shortest	1					1
Largest	1				2	3
Larger	1			1		2
Closest		1				1
Furthest		1				1
Lowest		2				2
Lower		1	1			2
Smallest		2	2	2	1	7
Earliest		1				1
Greater			2			2
Higher			1	2		3
Smaller			1			1
Latest			1			1
Longer			1			1
Narrower			1			1
Colder				2		2
Greatest				2		2
Lightest					3	3
Heaviest					1	1
Maximum					2	2
Total by year	7	10	15	9	12	54

Superlatives are a constant of reasoning papers, with new terms appearing every year so far. As you can see above, not many of the terms have appeared across more than one year’s worth of tests. This cannot happen forever and soon we will see repeats of terms above. We, as teachers, should be aware of these terms and prepare children sufficiently using explicit instruction – especially as their use has confused children in past years.

Children around the country were perplexed by this question. Had they known that ‘greatest’ denotes the most possible, children would have been better equipped to approach the question. Knowing the definition of this term would have made it easier to see that they needed to take 20 from 31, multiply it by 4 and add it to the existing amount.

Additionally, greatest appeared again in this same paper in another question worth 2 marks. That is a total of 4 marks that children could have lost because they did not understand a piece of mathematical vocabulary.

7 Strategies For Teaching Maths Language Effectively At KS2

It is obvious that language plays a crucial role in children accessing the reasoning papers and answering questions effectively, but what does that mean for our classroom practice?

Here are just 7 key components of explicit vocabulary instruction that are necessary for providing children with a rich and deep understanding of mathematical language:

1. Define mathematical vocabulary in every lesson alongside pictorial representations
2. Link language back to prior learning on topics in previous year groups
3. Explain synonyms, comparative and superlative terms and use them interchangeably on a regular basis
4. Avoid use of everyday language (e.g. don’t say borrow or take, say transfer)
5. Explain the connotations specific terms have (e.g. change means subtraction is needed)
6. Provide opportunity for children to reason in every lesson, both verbally and in writing
7. Structure our questioning so that it provokes thought and use of key terms in response (e.g. Sam thinks…Is he correct? Why?)

It is paramount that we enable children by providing them with the tools they need to access mathematical language. This represents the underlying fabric of mathematics teaching, whereby we must develop a child’s ability to reason.

Consequently, they will be able to interpret mathematical language successfully and begin to communicate their understanding in a structured manner.

---

Bibliography

• Adams, T. L. (2003) Reading mathematics: More than words can say. The Reading Teacher, 56, pp. 786–795.
• Beck, I.L., McKeown, M.G. and Kucan, L. (2013) Bringing words to life: Robust vocabulary instruction. Guilford Press.
• Riccomini, P. J. and Witzel, B. S. (2010) Response to intervention in mathematics. Thousand Oaks, CA: Corwin Press.