Cognitive Load Theory In The Classroom: How I Wish I’d Taught Maths (1)
Clare Sealy breaks down the essentials of cognitive load theory and how insights from cognitive science can improve teaching and learning in primary schools.
This article is part of a series published to help primary school teachers and leaders implement some of the teaching techniques derived from Craig Barton’s bestselling book How I Wish I’d Taught Maths. Links to the other 5 articles appear at the end.
If you’re short on time, just download the How I Wish I’d Taught Maths Crib Sheet which takes all the key points from all 6 blogs in a condensed form.
Craig Barton – The book behind the blog
As a primary school teacher, you might not have heard of Craig Barton. But if you’ve ever used any of the White Rose Diagnostic Questions, then you have Craig Barton (among others) to thank. Craig Barton is a legend among secondary school maths teachers.
As well as being behind Diagnostic Questions, he also created the incredibly useful website, Mr Barton Maths, has a very well-regarded podcast, the Mr Barton Maths Podcast and is a maths advisor for the TES. And now he has written an amazing book – How I Wish I’d Taught Maths.
The intended audience for his book is secondary maths teachers, but almost all of it is directly applicable to primary maths classrooms.
While some of the examples Craig uses are more obviously from the secondary curriculum, many involve fractions or percentages or geometry examples that might well be used in any Year 6 classroom.
Crib Sheet for How I wish I'd Taught Primary Maths
Download the key findings from research; share with your staff, your SLT, and at your next job interview!
Download Free Now!Systematic reflection on education research and cognitive science
However, the examples he uses are not what’s important about this book. What makes it essential reading is the systematic way in which Craig reflects on how learning about educational research, and in particular cognitive science, revolutionised how he taught maths.
Like many of us, Craig never really thought deeply about how children think and learn. It rarely featured in his initial teacher training or later CPD. He now realises that lots of his most cherished assumptions about what made good maths teaching were wrong. In How I Wish I’d Taught maths, Craig explains what cognitive science teaches us about how people learn and what the implications of that are for teaching maths more effectively.
All of this is completely transferable to a primary school context.
In this series of blogs, I will be outlining what Craig learnt from cognitive science and how it challenged his assumptions. I will also then share the teaching strategies he now uses instead, all of which you will find you can use when teaching your primary pupils maths.
In this first introduction blog, I look particularly at cognitive load theory as this is essential to all his findings about teaching maths.
Craig’s findings from research: How students think and learn
Cognitive scientist Daniel Willingham explains in Why Students Don’t Like School that knowing about the interplay between working memory and long-term memory is extremely useful when trying to teach anybody anything.

Working memory is where thinking actually happens
Working memory has limited capacity; it can hold and process roughly only four different items at a time.
In our ignorance of the limits of working memory, our teaching often overwhelms its capacity and expects learners to think about far too many things all at once. As a result of this overload, learning fails. The working memory simply cannot process the amount of information all at once and so ‘forgets’ some of it.
Read more
- What The Best Primary Maths Teachers Do: How You Can Learn From Them Fast
- Learning and Memory in The Classroom: What Teachers Should Know
- Teaching Low Ability Students Maths “Are We Bottom Set?”
Use the long-term memory to store facts
However, there is a way to work around the limitations of working memory. This is where knowing about long term memory comes in.
Unlike our working memories, our long-term memory has huge – almost infinite – capacity. It is here that we store information such as facts and procedures. This vast repository of information resides outside our conscious awareness but can be summoned into our working memory when needed.
Using processing such as interleaving, the long term memory enables us to bypass the problems presented by our small working memories. By stocking our long-term memories with knowledge in a well-organised, easily retrievable way and making recall of key aspects automatic, we improve retention and drastically cut down on the processing our poor, beleaguered working memories have to do.
This is especially important when teaching pupils topics such as the long multiplication method, which is made much simpler if one has the relevant multiplication facts stored in their long-term memory.
When we teach maths (or English, or Science, or anything else for that matter), we need to think about how we can ensure that what we teach makes the precarious journey from short term memory to long-term memory successfully. To do this we have to be mindful of cognitive load.
What is cognitive load?
Cognitive load is the term used in cognitive science to describe how much working memory capacity a topic or task takes up.
Cognitive overload is what happens if too many demands are placed on working memory at once.
Sweller’s Cognitive Load Theory (CLT) was developed in the late 1980s and has since become a key idea in educational psychology. The theory suggests that tasks apply three types of cognitive load onto our working memory:
- Intrinsic cognitive load
- Extraneous cognitive load
- Germane cognitive load
Intrinsic load is the mental effort the topic inherently takes; solving a complex equation is always more difficult than adding two numbers, for example.
Extraneous load is the effort added onto a task by the way it is presented, and is what we should seek to reduce when teaching.
Germane load is the effort we put into long term information processing – into schema acquisition for a topic when we have no prior knowledge of it.
John Sweller argued that instructional design theory could reduce extraneous load and free up processing capacity in learners considerably, resulting in better learning outcomes. This means teachers should use knowledge about cognitive load theory when developing learning tasks and learning materials to reduce extraneous cognitive load.
The theory has been further developed by researchers such as Paul Ayres, who developed the ‘split-attention effect’: the idea that when learners are required to process information from two different instructional materials at once (e.g. text and diagram), working memory load is increased considerably.
Cognitive load in a primary school maths context
Look at children learning to use the vertical addition algorithm with the following example:
+35
27
A child who has their number bonds stored in their long-term memory and knows that 5 + 7 = 12 can import that fact into their working memory without conscious effort.
None of that precious, finite capacity of working memory has to be wasted working out 5+7.
Whereas a child who does not know the answer automatically has to divert processing resources away from thinking about columns, value and regrouping, thinking instead about what 5+7 adds up to.
Their overloaded working memory can’t cope with this additional demand on top of everything else it is already thinking about, so it ‘forgets’ one of the important steps in the procedure. The child therefore gets the answer wrong.
Or even if the child doesn’t get the answer wrong, they do not learn how to use the vertical algorithm as a useful method they can generalise and transfer to other similar problems.
Reducing cognitive load in a primary school maths context
There are many different ways teachers can reduce cognitive load, and therefore improve the learning outcomes of pupils. These include:
- Worked examples – by providing pupils with step-by-step demonstrations, they can complete complex procedures with support
- Dual coding – when used well, the combination of audio and visual information can support pupil’s learning
- Consider the learning environment – too much information, such as music, busy classroom displays or distracting images or fonts can increase the cognitive load of a task
- Powerpoint – Many teachers use Powerpoints when teaching. These can be very helpful if used carefully to display essential information only when needed and if teachers make careful use of animations and images to enhance, not distract from learning.
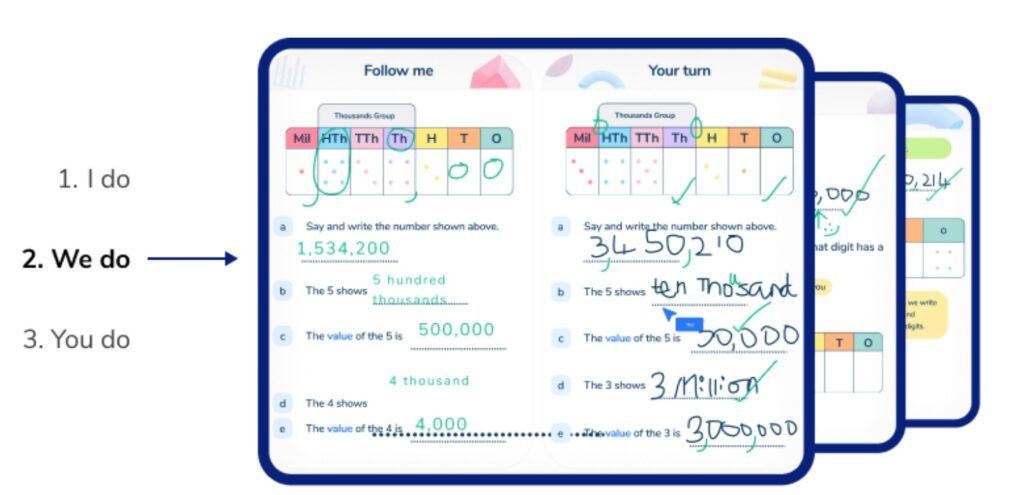
The slides used in Third Space Learning’s online one to one maths intervention have been designed to reduce cognitive load. From the slide design to lesson progression, we draw on our pedagogical knowledge and 10+ years’ experience as maths tutors to provide impactful, evidence-based maths tutoring.
The right amount of cognitive load for learning in primary maths
The main focus of How I Wish I’d Taught Maths is how to create just the right amount of cognitive load so that teaching can be as effective as possible.
A good example of this can be found here in this blog post on how to teach telling the time at KS1 and KS2, breaking it down to the simplest core elements.
Read more on cognitive load theory and the other cornerstones of evidence based teaching here:
- How To Learn Maths
- Differentiation in the Classroom: The 8 Strategies That Will Support Every Pupil To Reach A Good Standard
- Adaptive teaching
- Metacognition in the Classroom: A 7-Step Practical Approach To Primary Maths Teaching
- Quality First Teaching Checklist Of Strategies That Work
- Assessment for Learning
Other articles in the How I Wish I’d Taught Primary Maths series
- Explicit Direct Instruction And Using Rosenshine Principles of Instruction (2)
- Focused Thinking And Goal Free Questions (3)
- The 5 Stages Of Deliberate Practice In Teaching (4)
In the latter part of the book Craig considers how teaching can facilitate effective remembering. Having explained strategies for making sure learning makes it from the working memory to the long-term memory, the focus now turns to helping students use what they know.
This will be covered in the last two articles in this series.
- Critical Thinking Skills And Problem Solving Activities in KS2 (Same Surface, Different Deep Problems) (5)
- How Retrieval Practice Helps Long-Term Maths Skills (6)
How each article is structured
In each of these blogs, I ‘translate’ what Craig is saying into more primary maths relevant terms and use more primary maths curriculum focused examples than he has used.
Each blog has a section highlighting primary school maths context. Here I give practical examples of how Craig’s insights might be deployed in a primary classroom, rather than directly explaining what he says himself in his book.
Where I need to use the first person in sections these ‘translated’ sections, I have used ‘she’ rather than ‘he’ as a way of emphasizing that this is my interpretation of Craig’s work, rather than a summary of his own words or examples. It is not intended as a slight on male primary teachers! The references for the research Craig has used that I have mentioned are listed at the end of each blog under the title Sources of Inspiration.
Sources of Inspiration
- Barton C. (2018), How I Wish I’d Taught Maths
- Sweller, J (June 1988). “Cognitive load during problem solving: Effects on learning” (PDF)
- Ayres P., Cierniak G. (2012) Split-Attention Effect. In: Seel N.M. (eds) Encyclopedia of the Sciences of Learning. Springer, Boston, MA
- Sweller, J., van Merrienboer, J., & Paas, F. (1998). Cognitive architecture and instructional design. Educational Psychology Review, 10, 251-296.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly maths intervention programmes designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.





