The 5 Stages Of Deliberate Practice In Education: How I Wish I’d Taught Maths (4)

Clare Sealy looks at what deliberate practice in education means, and how you can use it to ensure pupils really know what you have taught them at primary school. Fourth in the ‘How I Wish I’d Taught Maths’ series.

This article is part of a series published to help primary school teachers and leaders implement some of the insights and teaching techniques derived from Craig Barton’s bestselling book How I Wish I’d Taught Maths. Links to the other 5 articles appear at the end.

In the introduction to this series, I outlined how Craig Barton in his book How I wish I’d taught maths described how he had changed his teaching strategies as the result of reading research around cognitive load theory in the classroom, and in particular, realising how easy it was to inadvertently prevent learning by overwhelming working memory through cognitive overload.  

By breaking down a complex process such as adding fractions into separate, individual skills and then deliberately practising those until they are easy, cognitive overload is avoided. Craig’s 5 stages of deliberate practice ensure that working memory can cope and so learning in transferred into the long-term memory.

Read more: Learning and Memory in the Classroom: What Teachers Should Know

Difference between novices and experts

Wiemann (2007) talks about ‘the curse of knowledge.’ What this means is that once you are really good at doing something, you approach it very differently to someone who is at the beginning of their learning.

You do not have to laboriously think through the process step by tiny step, because many of those steps have become completely automated and are retrieved without any effort at all on your part from your long term memory.

What is more, because the sub processes inherent in the activity have become automated, you find it hard to think about what they actually are. Everything seems so obvious to you it is difficult to step back and analyse what might not be at all obvious to a complete novice.

As a result, your rate of improvement in that subject tapers off unless you devote time to structured, incremental practice activities for it. 

Anders Ericsson and his colleagues developed the concept of deliberate practice in the 1990s, conducting a study of violinists of varying skill levels. Their conclusion was that the most skilled musicians had spent considerable time (the now-famous ‘10,000 hours’) in the structured practice with feedback and a view to improve in order to achieve ‘expert performance’ levels. 

Ericsson et al (2007) explained that to help novices become experts, teacher educators need to break learning down into individual sub-skills and deliberately practice each of those in turn, receiving feedback to help you improve your performance. Practising by itself, without this feedback, won’t help pupils improve.

The 5 stages of deliberate practice In education

When teaching something like adding fractions, we might tell children to find a suitable common denominator, then turn each fraction into the appropriate equivalent fraction, add the numerators together, then finally simplifying, where appropriate.

But this is a complex process involving several sub processes.

Many children are likely to struggle because they are being asked to think about too many things all at once. In order to prevent this, the 5 steps of deliberate practice help us break a complex process down into simpler processes and give time for pupils to practice each sub process until it is so easy it takes very little space in working memory.

The 5 principles of deliberate practice are:

1. Isolate the skill
2. Develop the skill
3. Assess the skill
4. Final performance
5. Practise again later, so that this in not forgotten

An important through-line for the 5 steps is purposeful practice – pupils must understand why they are practising certain skills, and not simply repeating a task because they have been told to.

1. Isolating the skill

To overcome the curse of knowledge, we need to think really hard about the sub processes that contribute to the overall complex process we want pupils to learn. For example, when adding fractions, pupils need to be able to:

1. Decide if fractions are in a form ready to be added (i.e. do they have the same denominator or not?)
2. If they don’t, decide what a suitable common denominator might be
3. Then transform both fractions into the appropriate equivalent form
4. Then add the numerators
5. Then decide if the answer needs simplifying or not
6. If necessary, simplify the answer

Instead of trying to teach this all at once, the point of deliberate practice in education is to pick these sub skills off one by one and practise until they are easy.

2. Developing the skill

Each separate skill then needs developing in turn. Some will be easier to teach and quicker to learn than others, but time spent here practising will reap dividends later as potential misconceptions will have been headed off at the pass.

It is also worth remembering that the rate at which skills develop will also vary from pupil to pupil. Use of questioning in the classroom and other differentiation in the classroom techniques is of great importance at this stage to ensure your low-ability students are able to develop alongside their higher ability peers.

So our first sub skill we isolated was deciding if fractions were in a form ready to be added together. Having demonstrated that you cannot add fractions if the denominators are different , pupils are then presented with a sorting exercise. Can these fractions be added? Yes or no?

1/3+1/3

1/3+ 2/3

2/3+1/5

2/3+2/5

4/5+5/4

3/8+3/4

1/1+1/15

1/50+1/500

Notice how some examples have the same numerator but different denominators. These are important to include as we need to know if pupils understand that it is having the same denominator that makes the difference. All we are doing here is sorting. We are not then going on to think about suitable denominators let alone adding.

Once that has been practised, and pupils can get that right effortlessly, then and only then can we move onto the next skill; deciding on an appropriate common denominator. All we will do at this point is decide what the appropriate denominator might be. We won’t actually work out any equivalent fractions at this point.

For example:

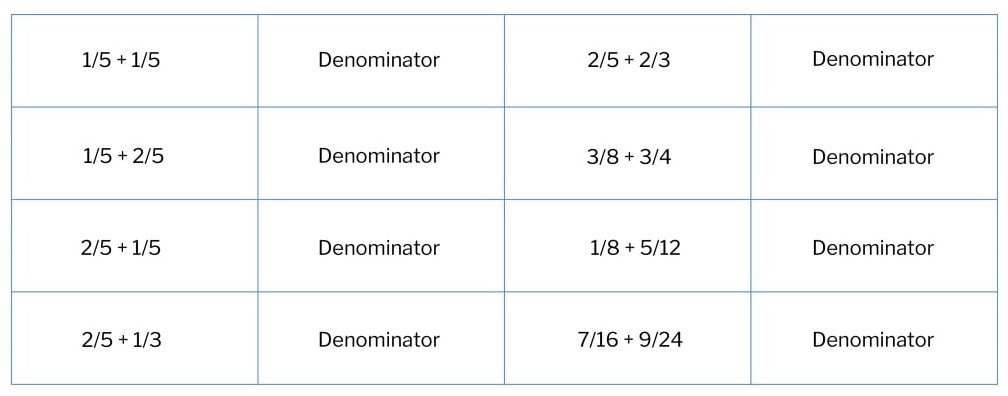
We would then do similar exercises for each of the remaining sub skills: transforming both fractions into the appropriate equivalent form, adding the two fractions together, deciding if they need simplifying and then – finally – simplifying.

3. Assess the skills

The next stage in the 5 stages of deliberate practice is to assess whether children have developed the sub-skill sufficiently securely to move on. Craig’s Diagnostic Questions are a useful resource here, as well as this piece on 4 Great Free KS2 Diagnostic Quizzes For Year 5 and 6.

4. The final performance

Once we know the children can do each of the separate sub-skills, we are ready to put them all together and add those fractions! At this point, the teacher can use direct instruction.

5. Retrieval practice later

We will also need to include spaced repetition to come back and check children can still remember how to do whatever we have taught them in weeks and months to come. No one wants to find that the dreaded summer slide has left pupils with no memory whatsoever of topics covered even just before the holidays!

It’s one thing being able to perform a skill in the same lesson in which it was taught. It is another thing entirely to be able to still do that skill weeks after that unit of work has finished.

The vexed issue of long term retention will be covered in the final of this series on blogs, when we turn our attention to retrieval practice and automaticity.

Read more: A Practical Guide To Rosenshine’s Principles of Instruction

Deliberate practice in education: Translating this to a primary school context

For primary aged children, in the particular example that Craig shares of adding fractions, I think there are more sub-skills needing developing here than Craig has identified. Many primary children would struggle with the ‘finding a suitable denominator stage’, so we would need to isolate and practise the skills of finding lowest common multiples first.

Craig has made the reasonable assumption given his secondary context that secondary aged children would already be able to do this, and is part of what he would have assessed before beginning fractions in the first place.

We cannot make that assumption with younger children.

If children cannot identify lowest common multiples with ease, the whole adding fractions enterprise is doomed. This means of course, that children have to know their times tables really well. If they don’t, moving on to fractions is pretty pointless.

So let’s isolate the skills involved in finding lowest common multiples and develop those before proceeding further.

First of all, a sorting exercise: multiple or not multiple?

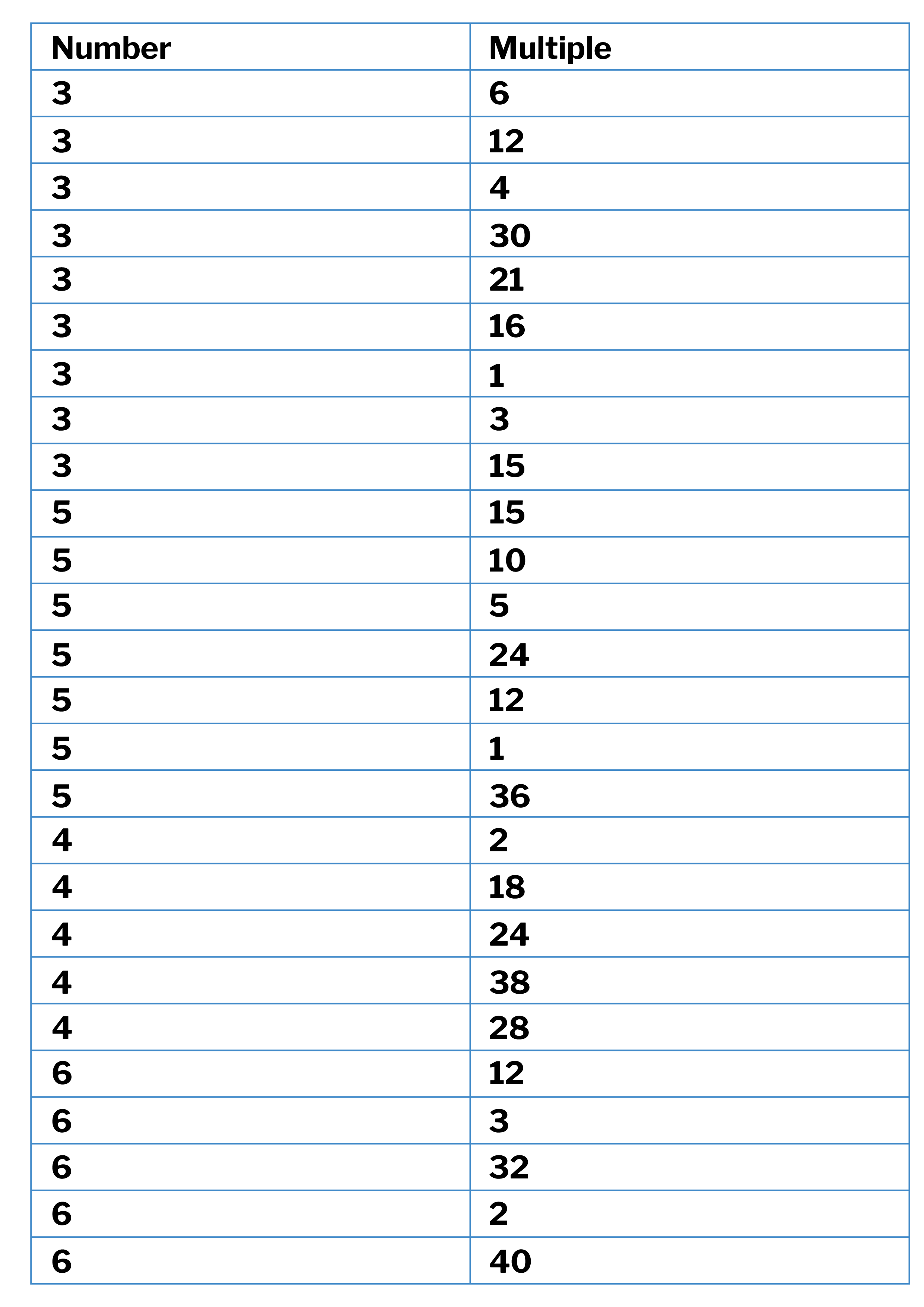
Particularly important in this list are the examples where a factor is given rather than a multiple as this is a common source of confusion. It is really important that pupils understand that 2 is not a multiple of 4 (although 4 is a multiple of 2) or else there will be trouble ahead.

It is also important that they realise that 5 is a multiple of 5 (and so on), as this will also be important when deciding on the common lowest multiple for 8 and 4. Pupils often think it’s 16, or 32, rather than 8.

Having developed this skill, then we turn to finding common multiples.

Circle the common multiples

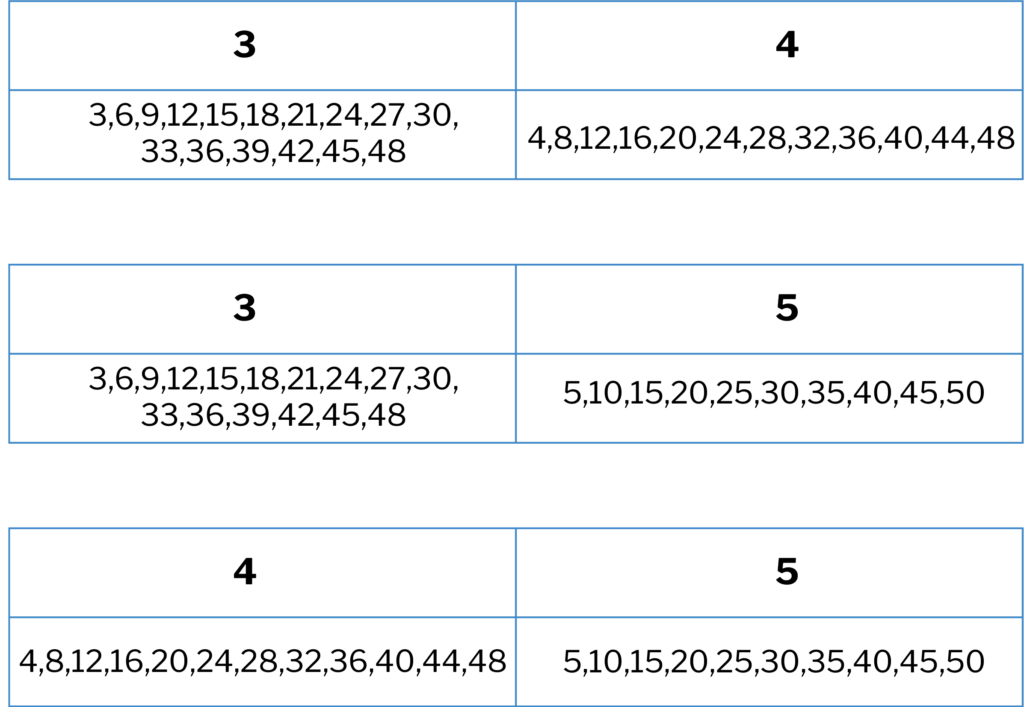
When pupils can do this effortlessly, you can adapt this exercise so that having identified all the multiples, pupils then go on to decide the lowest common multiple.

When pupils can identify the lowest common multiple having been given a list, the next step is to be able to do so using the ‘list’ in one’s head. This will only work of course if such a mental list exists and pupils can retrieve table facts automatically.

Circle the lowest common multiple for the following pairs of numbers

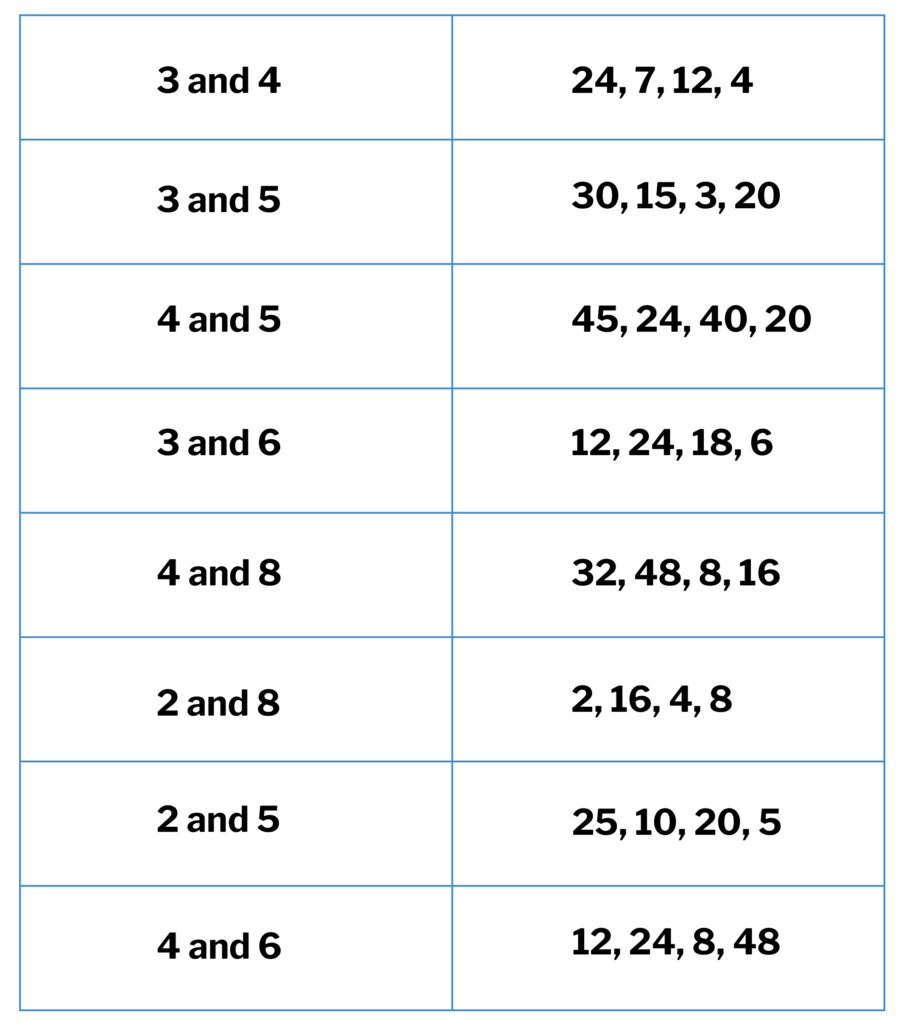
Once this is secure, we are ready for the next step.

Transforming fractions, using equivalent fractions.

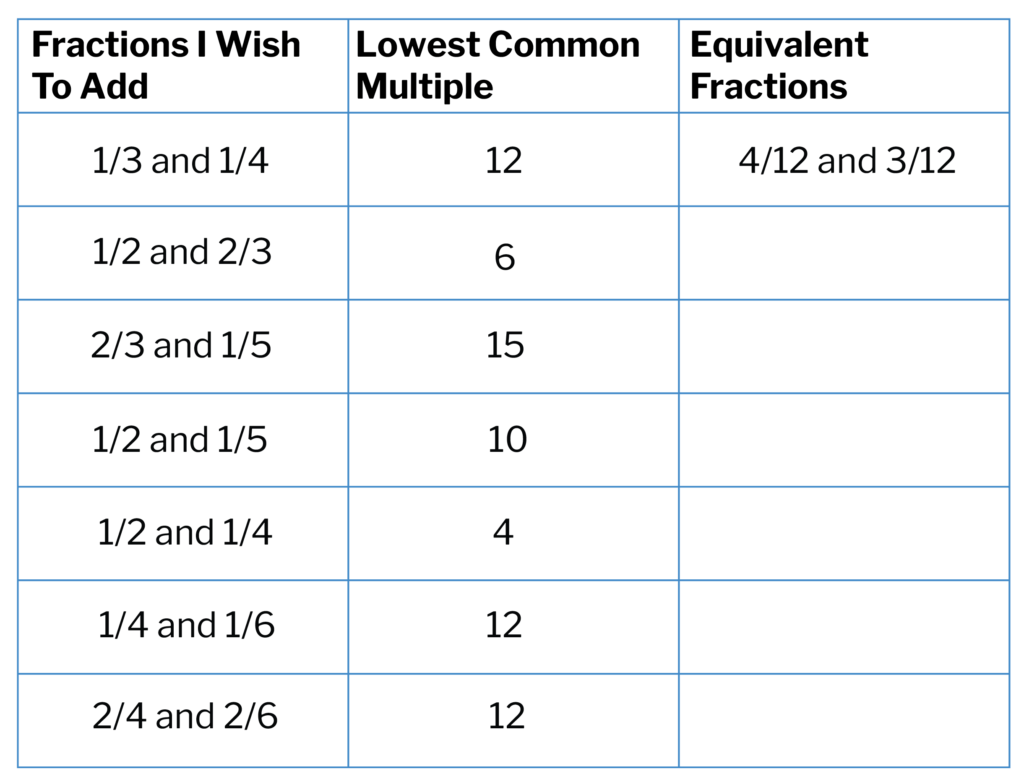
Once all these sub steps are secure, actually adding the transformed fractions is a breeze. And of course all the ground work has been already done to learn how to subtract fractions too. The same exercise could also be used subsequently, with children having to fill in the second column as well. Gradually fading scaffolding away once processes are more secure is an important step to build independence.

This approach is worth the time it takes

Going through each sub skill in such detail might seem laborious. But it is much better to do this and avoid misconceptions along the way than have to unpick them later because you have underestimated how complex learning something actually is, cursed as you are by your teacher expertise.

At first, it can be hard to really break the learning down into small enough steps, as for us experts, it all seems so obvious. A good way to explore this is to use staff meeting time to try to isolate all the sub skills involved in a particular process, then swap compare lists with colleagues and see what you’ve missed out.

Using deliberate practice in education may seem tough at first, but it is a quality first teaching strategy that is certainly worth it in the long run.

I have broken down teaching telling the time into small sub-steps in another article for KS1 and KS2 teachers.

Sources of inspiration

• Weimann, C. (2007) ‘The curse of knowledge’, or why intuition about teaching often fails’, APS News 16 (10) (no pagination)
• Ericsson, K.A.. Prietula, M. J. and Cokely, E.T. (2007) ‘The making of an expert’, Harvard Business Review 85 (7/8) pp.114-121
• Ericsson, K. A., Krampe, R. T., & Tesch-Römer, C. (1993). The role of deliberate practice in the acquisition of expert performance. Psychological Review, 100(3), 363–406 

---

Read more:

• Goal Free Problems And Focused Thinking: How I Wish I’d Taught Primary Maths (3)
• Metacognition In The Classroom: A 7-Step Practical Approach To Primary Maths Teaching
• Developing Growth Mindset In The Classroom At KS2: 10 Key Principles And Your Classroom Contract