25 Year 6 Algebra Questions And Answers: KS2 Assessment Preparation
Here are 25 Year 6 SATs algebra questions designed to cover the algebraic concepts pupils are likely to encounter in the Key Stage 2 SATs.
In addition to these questions, we look in depth at the key algebraic vocabulary children should be familiar with when tackling algebraic questions ahead of the maths SATs.
Generally, algebra appears in the KS2 reasoning papers and not the Year 6 arithmetic questions. Usually appears less frequently in KS2 maths SATs papers than other national curriculum strands such as the four operations, place value and percentages, decimals and fractions questions.
But, it is still essential that Year 6 pupils are confident in addressing algebraic questions for their KS2 assessments so they can develop their understanding of algebra in KS3 and at GCSE.
Why are Year 6 algebra questions important in Key Stage 2?
Understanding basic algebraic concepts and formulas in Key Stage 2 helps to lay the foundations for more complex algebra in KS3, at GCSE and beyond. It also helps to develop children’s problem solving, critical thinking and logic.
Often, algebra may evoke anxiety in children before they even enter year 6 — they aren’t aware that they have been engaging with basic algebraic concepts since Key Stage 1.
For example, missing number calculations in Year 1, such as 3 + \_ = 10 are the starting blocks for algebraic expressions in Year 6, such as x + 3 = 10 .
As educators, it is important to make pupils aware of this relationship, helping to reduce the anxiety associated with algebra.
Similarly to ratio questions, it helps to link algebraic concepts to real-life situations when teaching algebra in KS2. This helps to enhance pupils’ understanding.
Demonstrating how to apply algebra in Year 6 can help pupils independently solve problems in everyday scenarios and grasp its practical relevance.
For instance, solving the equation 3x = 24 may initially seem quite abstract. But when asked to calculate the cost of one apple, when the cost of 3 apples is 24p, pupils can contextualise the question and make connections to this algebraic concept.
Providing children with concrete resources, visual representations and real-life situations is vital in the teaching of algebra. This approach helps pupils break down the abstract nature of algebra and develop a conceptual understanding.
Key terminology for Year 6 SATs algebra
Children need to have an understanding of algebra terminology in order to secure their knowledge of algebraic concepts.
Year 6 pupils will need to have an understanding of the following key terms:
- Algebra: The use of letters and symbols to represent numbers, when we don’t know the value in an equation.
For example, y + 5 = 10
- Variable: A symbol (usually a letter), used to represent an unknown or changing quantity.
For example, in the number sentence 2x + 5 = 19, \; x is the variable
- Term: A single mathematical expression separated by addition or subtraction in an algebraic expression.
For example, in 4x + 6, \; 4x and 6 are terms
- Unknown: The value you are trying to work out is shown as a letter.
For example, in the number sentence 3x + 4 = 13, \; x is the unknown
- Expression: A mathematical sentence using numbers and/or variables.
For example, 3x + 7 is an expression.
- Equation: a mathematical statement or expression that contains two equal sides separated by an equals sign.
For example, 2y + 4 = 12 or 2y + 4 = 3x + 3
- Formula: Algebra uses formulas, which refer to a mathematical rule or relationship that uses letters to represent amounts which can be changed.
For example, 7 + x = 10
- One-step equation: An equation which can be solved in only one step.
For example, x + 7 = 15
- Two-step equation: An algebraic equation that takes you two steps to solve.
For example, 3x + 5 = 11
- Substitution: Replacing variables in an algebraic expression with their numerical values.
For example, x + 3 = 13 is equal to 10 + 3 =13
- Pair of unknowns: A number sentence where there are two unknown values.
For example, x + y = 12 and x is 3 times greater than y. Both x and y are unknowns.
- Enumerate: Finding all possible answers to an algebraic problem and making a complete list of answers.
For example, x + y = 5
| Where x = \; | \quad \;\; y= \;\; \quad |
| 1 | 4 |
| 2 | 3 |
| 3 | 2 |
| 4 | 1 |
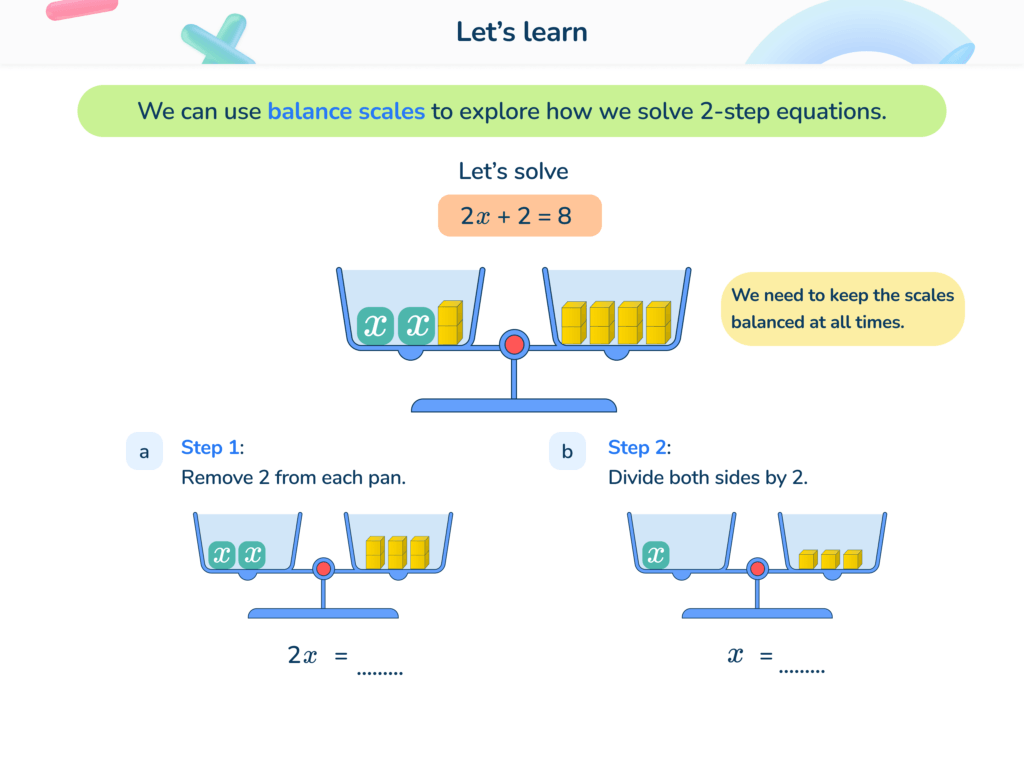
- Balancing equations: Performing operations on both sides of a number sentence to find the missing value.
For example, where 3x +12 = 24 start by subtracting 12 from both sides of the equation.
24 - 12 =
3x = 12
12 ÷ 3 = 4
x = 4
200 arithmetic and reasoning questions for Year 6
Download 100 free arithmetic questions and 100 free reasoning questions for Year 6. Includes answers and mark scheme.
Download Free Now!How do these Year 6 algebra questions help pupils prepare for the KS2 SATs?
These Year 6 algebra questions cover the breadth of the national curriculum. They have been designed by a math expert to cover the array of algebra SATs questions pupils may encounter in the KS2 SATs.
All problems, including algebra word problems, are contextualised to represent real-life scenarios. This helps pupils take the abstract concept and relate it to a familiar situation.
Practising a variety of algebra questions helps familiarise pupils with the question formats they will encounter in the KS2 SATs and develop confidence in their strategies for solving them.
Each question in the sequence becomes progressively harder, providing children with the opportunity to deepen their understanding of algebra. This also means questions will challenge those pupils who are working at greater depth.
25 Year 6 algebra questions and answers
Year 6 algebra questions: using simple formulae
According to the national curriculum, pupils must be able to use and apply basic mathematical formulas to solve problems. To do this, they must be familiar with simple formulas and recognise the relationship between variables.
For example, the formula to find the area of a rectangle: Area = length x width
Question 1: using simple formulae
Calculate the value of each letter below:
4a = 12
7b = 63
9c = 27
Answer: a = 3, \; b = 9, \; c = 3
a. 12 ÷ 4 = 3
b. 63 ÷ 7 = 9
c. 27 ÷ 9 = 3
Question 2: using simple formulae
Calculate the value of the letter in the equation below:
4x + 8 = 24Answer: x = 4
4x = 16 4 \times 4 = 16 x = 4
Question 3: using simple formulae
The formula for calculating the area of a rectangle is A = ab ( A is the area and ab are adjacent sides).
A rectangle has sides with a length of 7.2cm and a width of 3.8cm. What is the area?
Answer: 27.36 \, cm^2
7.2 \, cm \times 3.8 \, cm = 27.36 \, cm^2
Question 4: using simple formulae
The formula for converting kilometres (k) to miles (m) is: k = m \times 8÷5
Use this formula to convert 20 miles into kilometres.
Answer: 32 \, km
20 \times 8 ÷ 5 = 160 ÷ 5 = 32 \, km
Question 5: using simple formulae
The formula for calculating the area of a triangle is \cfrac{1}{2} \, (b \times h)
What would be the height of a triangle with an area of 300 \, cm^2 and a base of 15 \, cm ?
Answer: 4 \, cm
\cfrac{1}{2} \times 15 \times h = 30 7.5 \times h = 30 h = 4More Year 6 algebra questions: Year 6 Forming Expressions Worksheets
Year 6 algebra questions: generate and describe linear number sequences
By the end of Year 6, pupils should be able to create and articulate linear number sequences where there is a constant difference between consecutive terms.
Pupils should also be able to create sequences where they are given the first term and a constant difference to continue expanding the sequence.
Question 6: linear number sequences
What are the next two terms in this sequence?
37, 44, 51, 58, ,
Answer: 65, 72 (+ 7)
Question 7: linear number sequences
Fill in the missing numbers in this sequence:
98, , , 71
Answer: 98, 89, 80, 71
Question 8: linear number sequences
The formula 4n + 3 is used to generate a sequence,
Give the first 5 numbers of the sequence.
Answer: 7, 11, 15, 19, 23
Question 9: linear number sequences
Here is a linear sequence:
4, 11, 18, 25
- What is the n th term?
- What is the 15th term?
Answer:
- 7n - 3
- 102
Question 10: linear number sequences
Ben has £28 at the start of the month. He spends 30p everyday day in January. How much does he have at the end of the month?
Answer: £18.70
30 x 31 = 930 (£9.30)
£28 – £9.30 = £18.70
Year 6 algebra questions: express missing number problems algebraically
A requirement of the national curriculum is for Year 6 pupils to be able to solve problems involving unknown values using algebraic expressions or algebraic equations.
Children first encounter missing number problems in KS1. For example: 3 + \_ = 10 . By the end of KS2, pupils progress to writing missing expressions and solving equations for a range of real-life problem solving scenarios.
Question 11: express missing number problems
12 more than a number is 33. Write an expression for this, using n to represent the number:
Answer: n + 12 = 33
Question 12: linear number sequences
What needs to be added to 27 to make 59?
Show the expression and the value of n.
Answer: 27 + n = 59 \quad \;
59 - 27 = 32 n = 32
Question 13: linear number sequences
A function machine multiplies by 4 and then adds 5. What would be the expression if x was put into the function machine?
Answer: 4x + 5
Question 14: linear number sequences
An electrician charges £15 per hour and £25 for a call out.
What is the formula to express this calculation? (Use c for the cost and h for hour)
Answer: C = 15h + 25
Question 15: linear number sequences
A painter charges £14 per hour, but in December offers a discount of £8.
- Write a formula to express this calculation (use c for cost and h for hour)
- How much would it cost to hire the painter for 8 hours in December?
Answer: a. C = 14h - 8
Answer: b. £104
(14 x 8)-8 = 104
Year 6 algebra questions: find pairs of numbers that satisfy an equation with two unknowns
Equations with two unknowns involve two variables which are usually represented by letters such as x and y.
Each equation expresses the relationship between the variables. Pupils should be able to identify and apply pairs of numbers to the two variables in order to solve the equation.
Question 16: pairs of numbers for two unknown values
Find a possible solution for the following equation:
3x + 2y = 25Answer: x = 6 , \; y = 3 (other possible solutions can be given)
Question 17: pairs of numbers for two unknown values
Find a possible solution for this equation:
6a + 10 = 4bAnswer: a = 3, \; b = 7 (other possible solutions can be given).
Question 18: pairs of numbers for two unknown values
x is 3 times the value of y . What are the values of x and y?
Answer: x = 27, \; y = 9
Question 19: pairs of numbers for two unknown values
If z = 25 give one possible value of x and y?
Answer: x = 6, \; y = 3.5 (other possible answers may be given)
Question 20: pairs of numbers for two unknown values
Mason has some 50p and 20p coins. Altogether he has £2.40.
How many of each coin could he have?
Can you find the 2 possible solutions?
Answer: 2 x 50p and 7 x 20p
Or 4 x 50p and 2 x 20p
More questions: Year 6 Finding Pairs of Values Worksheet
Year 6 algebra questions: Enumerate possibilities of combinations of 2 variables
Enumerate possibility questions involve systematically listing and exploring various combinations of values for two variables.
By the end of KS2, pupils should be able to methodically consider various combinations of values for two variables.
Question 21: enumerate possibilities of combinations
The total of two numbers is 15. Both numbers are between 3 and 12.
Find all possible combinations that the two numbers could be:
Answer: 4 + 11, 5 + 10, 6 + 9, 7 + 8
Question 22: enumerate possibilities of combinations
The difference between two numbers is 7. Both numbers are between 18 and 30.
What could the numbers be?
Find all the possible combinations.
Answer: 30 – 23, 29 – 22, 28 – 21, 27 – 20, 26 – 19
Question 21: enumerate possibilities of combinations
Year 6 has a maths test every week and there are 15 questions on each test.
Mason worked out he scored double in the last week of term compared to the first week of term.
How many correct answers might Mason have scored in the first week?
Give all the possibilities.
Answer: 1, 2, 3, 4, 5, 6 or 7
Question 22: enumerate possibilities of combinations
Find all the possible combinations, where x and y are whole numbers:
x + y = 41x < 17 and y < 27
Answer: 26 + 15, 25 + 16
Question 23: enumerate possibilities of combinations
d is an odd number < 16 and e is a multiple of 3 < 13
What could the values of d and e be?
List all the possibilities.
Answers: 3 x 15 + 2 x 3, 3 x 13 + 2 x 6, 3 x 11 + 2 x 9, 3 x 9 + 2 x 12
More Year 6 algebra worksheets and algebra resources
- Year 6 Algebra and Measures Worksheet
- Year 6 Forming and Solving One Step Equations Worksheet
- Year 6 Forming and Solving Two Step Equations Worksheet
- Year 6 Algebra Recap
- 15 Algebra Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included
FAQs
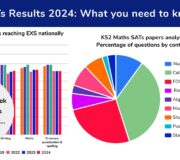
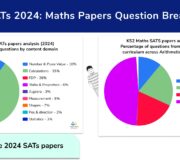
While algebra does appear in Year 6 SATs questions, there are a lower percentage of algebra questions in the KS2 exams than some of the other content domains from the maths national curriculum.
Over the last 5 years, algebra questions have made up between 4\% and 9\% of the Key Stage 2 maths assessments.
Algebra is explicitly taught to children from Year 6 (age 10 and 11 ) onwards. But children are introduced to basic algebra concepts, such as missing number questions, in primary school at a much younger age.
Pupils are introduced to the concept of algebra in Year 6. According to the national curriculum, by the end of Key Stage 2, pupils should be able to:
• Use simple formulae
• Generate and describe linear number sequences
• Express missing number problems algebraically
• Find pairs of numbers that satisfy an equation with two unknowns
• Find enumerate possibilities of combinations of two variables
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the SATs revision programme or request a personalised quote from your school to speak to us about your school’s needs and how we can help.