300 Primary School Maths Word Problems: Includes Examples And Answers
Solving word problems at KS1 and KS2 is an essential part of the new maths curriculum. Here you can find expert guidance on how to solve maths word problems as well as examples of the many different types of word problems primary school children will encounter with links to hundreds more.
What is a word problem?
A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
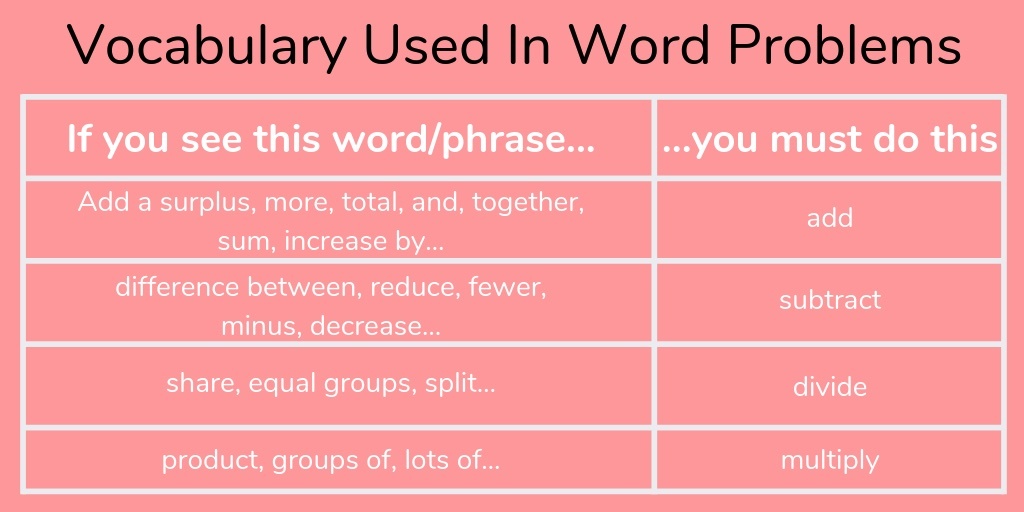
This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem.
For example:
Importance of word problems within the national curriculum
The National Curriculum states that its mathematics curriculum “aims to ensure that all pupils:
- become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately;
- reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
- can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.”
To support this schools are adopting a ‘mastery’ approach to maths
The National Centre for Excellence in the Teaching of Mathematics (NCETM) have defined “teaching for mastery”, with some aspects of this definition being:
- Maths teaching for mastery rejects the idea that a large proportion of people ‘just can’t do maths’.
- All pupils are encouraged by the belief that by working hard at maths they can succeed.
- Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other.
- Significant time is spent developing deep knowledge of the key ideas that are needed to underpin future learning. The structure and connections within the mathematics are emphasised, so that pupils develop deep learning that can be sustained.
(The Essence of Maths Teaching for Mastery, 2016)
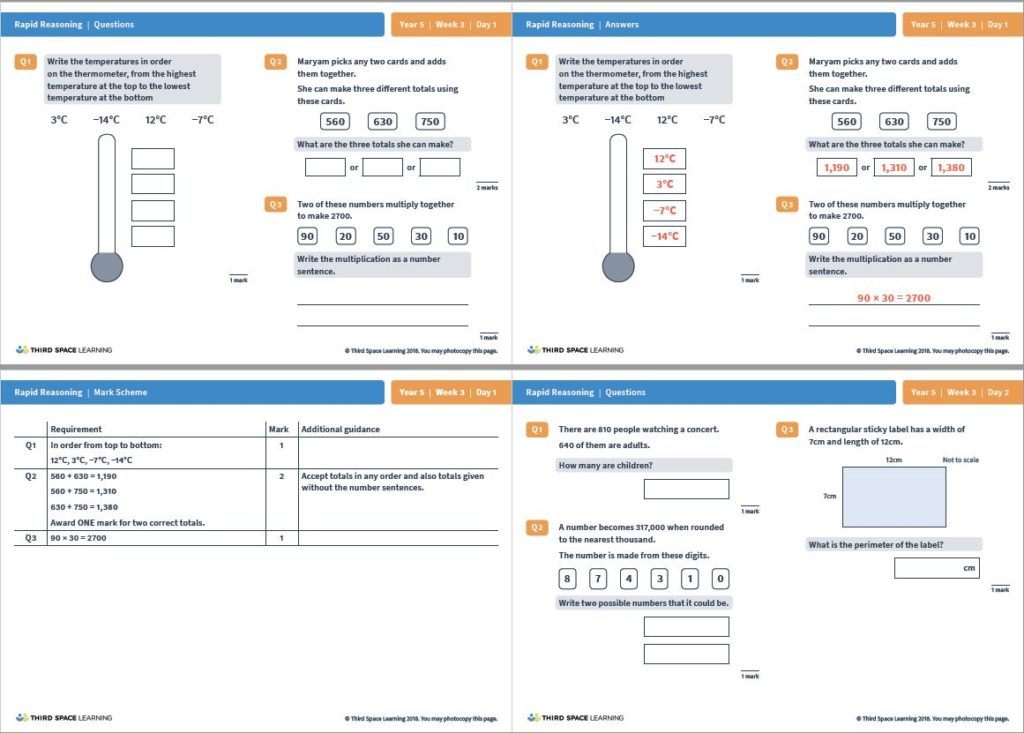
Year 3 to 6 Rapid Reasoning Worksheet for Weeks 1-6
Download for FREE 6 weeks of Rapid Reasoning worksheets. That include six weeks of daily reasoning and problem-solving questions for years 3, 4, 5 and 6!
Download Free Now!Mastery helps children to explore maths in greater depth
One of NCETM’s Five Big Ideas in Teaching for Mastery (2017) is “Mathematical Thinking: if taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others”.
In other words – yes, fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learnt the number skills appropriate to their level/age, they should be progressed to the next level/age of number skills.
The mastery approach encourages exploring the breadth and depth of these concepts (once fluency is secure) through reasoning and problem solving.
See the following example:
| Year 6 objective | Fluency | Reasoning | Problem solving |
|---|---|---|---|
| Solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why. | 7,208 females attended a concert as well as 8,963 males. There were originally 20,000 seats on sale. How many empty seats were there at the concert? | Abdul says, “If I add any two 4-digit numbers together, it will make a 5-digit number.” Do you agree? Explain why. | Three pandas are eating bamboo sticks. There are 51 altogether. They all eat an odd number of sticks. How many bamboo sticks did they each eat? How many different ways can you do it? |
What sort of word problems might my child encounter at school?
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”. The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
|---|---|---|---|---|---|
| Number and place value | 6 | 9 | 7 | 5 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |

Meet Skye, the voice-based AI tutor making maths success possible for every student.
Built by teachers and maths experts, Skye uses the same pedagogy, curriculum and lesson structure as our traditional tutoring.
But, with more flexibility and a lower cost, schools can scale online maths tutoring to support every student who needs it.
Watch Skye in actionHow to teach children to solve word problems?
Here are two simple strategies that can be applied to many word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
Let’s see how this can be applied to a word problem to help achieve the answer.
Solving a simple word problem
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
The bar model is always a brilliant way of representing problems, but if you are not familiar with this, there are always other ways of drawing it out.
Read more: What is a bar model
For example, for this question, you could draw 28 pupils (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
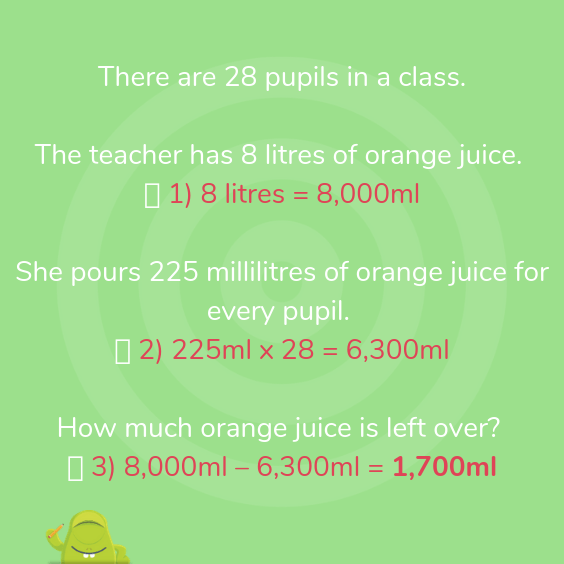
Solving a more complex word problem
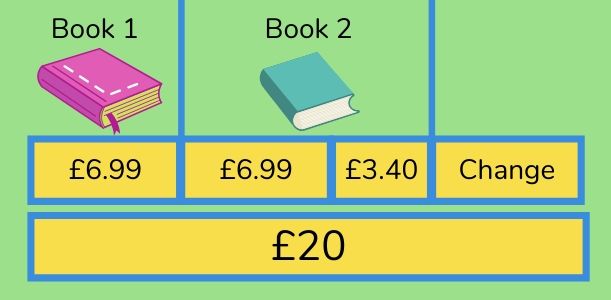
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book.
She pays using a £20 notes.
What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
She pays using a £20 note.
What change does Mara get? 2) £20 – £17.38 = £2.62
Maths word problems for years 1 to 6
The more children learn about maths as the go through primary school, the trickier the word problems they face will become.
Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each primary year group
Word problems in Year 1
Throughout Year 1 a child is likely to be introduced to word problems with the help of concrete resources (pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.
An example of a word problem for Year 1 would be:
Chris is going to buy a cake for his mum which costs 80p. How many 20p coins would he need to do this?
Word problems in Year 2
Year 2 is a continuation of Year 1 when it comes to word problems, with children still using concrete maths resources to help them understand and visualise the problems they are working on
An example of a word problem for Year 2 would be:
A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?
Word problems in Year 3
With word problems for year 3, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the four operations such as addition and subtraction word problems, multiplication and division problems too.
This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.
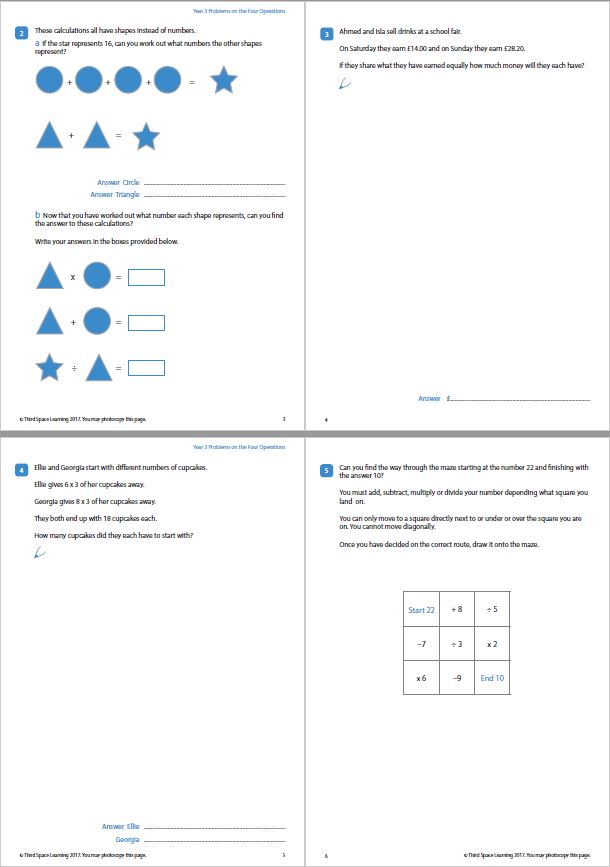
Year 3 word problem: Geometry properties of shape
Shaun is making 3-D shapes out of plastic straws.
At the vertices where the straws meet, he uses blobs of modelling clay to fix them together
Here are some of the shapes he makes:
| Shape | Number of straws | Number of blobs of modelling clay |
|---|---|---|
| A | 8 | 5 |
| B | 12 | 8 |
| C | 6 | 4 |
One of Sean’s shapes is a cuboid. Which is it? Explain your answer.
Answer: shape B as a cuboid has 12 edges (straws) and 8 vertices (clay)
Year 3 word problem: Statistics
Year 3 are collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.

Answer: a) 9 b) 3 pebbles drawn
Top tip
By the time children are in Year 3 many of the word problems, even one-step story problems tend to be a variation on a multiplication problem. For this reason learning times tables becomes increasingly essential at this stage. One of the best things you can do to help with Year 3 maths at home is support your child to do this. You can also help children while they are developing this skill by providing 100 squares to help them solve these word problems.
Word problems in Year 4
At this stage of their primary school career, children should feel confident using the written method for each of the four operations.
Word problems for year 4 will include a variety of problems, including 2-step problems and be children will be expected to work out the appropriate method required to solve each one.
Year 4 word problem: Number and place value
My number has four digits and has a 7 in the hundreds place.
The digit which has the highest value in my number is 2.
The digit which has the lowest value in my number is 6.
My number has 3 fewer tens than hundreds.
What is my number?
Answer: 2,746
Word problems in Year 5
One and 2-step word problems continue with word problems for year 5, but this is also the year that children will be introduced to word problems containing decimals.
These are some examples of Year 5 maths word problems.
Year 5 word problem: Fractions, decimals and percentages
Stan, Frank and Norm are washing their cars outside their houses.
Stan has washed 0.5 of his car.
Frank has washed 1/5 of his car.
Norm has washed 5% of his car.
Who has washed the most?
Explain your answer.
Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.05)
Word problems in Year 6
Word problems for year 6 shift from 2-step word problems to multi-step word problems. These will include fractions, decimals, percentages and time word problems.
Here are some examples of the types of maths word problems Year 6 will have to solve.
Year 6 word problem – Ratio and proportion
This question is from the 2018 key stage 2 SATs paper. It is worth 1 mark.
The Angel of the North is a large statue in England. It is 20 metres tall and 54 metres wide.
Ally makes a scale model of the Angel of the North. Her model is 40 centimetres tall. How wide is her model?
Answer: 108cm
Year 6 word problem – Algebra
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
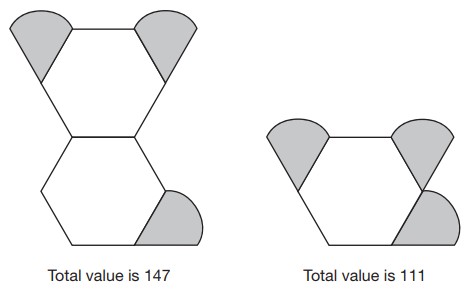
Amina is making designs with two different shapes.
She gives each shape a value.
Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
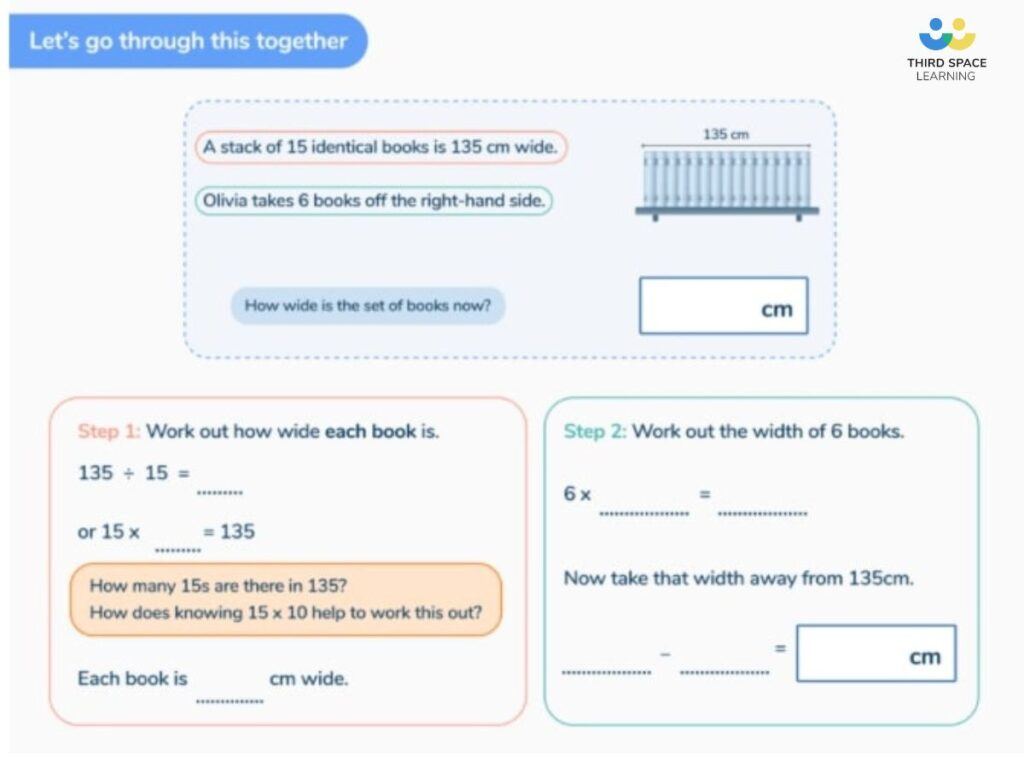
Year 6 word problem: Measurement
This question is from the 2018 KS2 SATs paper. It is worth 3 marks as it is a multi-step problem.
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
Answer: 1.7 litres or 1,700ml
Topic based word problems
The following examples give you an idea of the kinds of maths word problems your child will encounter for each of the 9 strands of maths in KS2.
Place value word problems
Place value word problem Year 5
This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37
Download free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction word problem Year 3
In Year 3 pupils will solve addition word problems and subtraction word problems with 2 and 3 digits.
Sam has 364 sweets. He gets given 142 more. He then gives 277 away. How many sweets is he left with? Answer: 229
Download free addition and subtraction word problems for Years 3, 4, 5 and 6
Addition word problem Year 3
Alfie thinks of a number. He subtracts 70. His new number is 12. What was the number Alfie thought of? Answer: 82
Subtraction word problem Year 6
The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC
More here: 25 addition and subtraction word problems
Multiplication and division word problems
Multiplication and division word problem Year 3
A baker is baking chocolate cupcakes. She melts 16 chocolate buttons to make the icing for 9 cakes. How many chocolate buttons will she need to melt to make the icing for 18 cakes? Answer: 32
Multiplication word problem Year 4
Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108
Download free multiplication word problems for Years 3, 4, 5 and 6
Division word problem Year 6
A factory produces 1,692 paintbrushes every day. They are packaged into boxes of 9. How many boxes does the factory produce every day? Answer: 188
Download our free division word problems worksheets for Years 3, 4, 5 and 6.
More here: 20 multiplication word problems
More here: 25 division word problems
Free resource: Use these four operations word problems to practise addition, subtraction, multiplication and division all together.
Fraction word problems
Fraction word problem Year 5
At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3
Download free fractions and decimals word problems worksheets for Years 3, 4, 5 and 6
More here: 28 fraction word problems
Decimals word problem Year 4 (crossover with subtraction)
Which two decimals that have a difference of 0.5? 0.2, 0.25, 0.4, 0.45, 0.6, 0.75. Answer: 0.25 and 0.75
Download free decimals and percentages word problems resources for Years 3, 4, 5 and 6
Percentage word problem Year 5
There are 350 children in a school. 50% are boys. How many boys are there? Answer: 175
Measurement word problem Year 3 (crossover with subtraction)
Lucy and Ffion both have bottles of strawberry smoothie. Each bottle contains 1 litre. Lucy drinks ½ of her bottle. Ffion drinks 300ml of her bottle. How much does each person have left in both bottles? Answer: Lucy = 500ml, Ffion = 300ml
More here: 25 percentage word problems
Money word problem Year 3
James and Lauren have different amounts of money. James has twelve 2p coins. Lauren has seven 5p coins. Who has the most money and by how much? Answer: Lauren by 11p.
More here: 25 money word problems
Area word problem Year 4
A rectangle measures 6cm by 5cm.

What is its area? Answer: 30cm2
Perimeter word problem Year 4
The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many metres has she swum? Answer: 108m
Ratio word problem Year 6 (crossover with measurement)
A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
More here: 24 ratio word problems
Bodmas word problem Year 6
Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
50 – 10 × 5 =
50 – 10 × 5 =
Volume word problem Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
How important are word problems when it comes to the SATs?
In the KS1 SATs, 58% (35/60 marks) of the test is comprised of maths ‘reasoning’ (word problems).
In KS2, this increases to 64% (70/110 marks) spread over two reasoning papers, each worth 35 marks. Considering children have, in the past, needed approximately 55-60% to reach the ‘expected standard’, it’s clear that children need regular exposure to and a solid understanding of how to solve a variety of word problems.
Children have the opportunity to practice SATs style word problems in Third Space Learning’s online one-to-one SATs revision programme. Personalised to meet the needs of each student, our programme helps to fill gaps and give students more confidence going in to the SATs exams.
Remember: The word problems can change but the maths won’t
It can be easy for children to get overwhelmed when they first come across word problems in KS2, but it is important that you remind them that whilst the context of the problem may be presented in a different way, the maths behind it remains the same.
Word problems are a good way to bring maths into the real world and make maths more relevant for your child, so help them practise, or even ask them to turn the tables and make up some word problems for you to solve.
This article while written by a teacher for teachers is also suitable for those at home supporting children with home learning. More free home learning resources are also available.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about a primary school maths tutor for your school.