What Is A Unit Fraction? Explained For Primary Parents
In this post we will be explaining what a unit fraction is, what they mean, and providing you with some questions you can use to test your KS2 child’s skills when it comes to unit fractions.
This blog is part of our series of blogs designed for parents supporting home learning and looking for home learning resources during the Covid-19 epidemic.
What is a unit fraction?
A unit fraction is any fraction with 1 as its numerator (top number), and a whole number for the denominator (bottom number).
Examples of unit fractions include:
Understanding and Comparing Fractions Worksheets
Download these FREE understanding and comparing fractions worksheets for Year 3 pupils, intended to help pupils independently practise what they've been learning.
When will my child learn about unit fractions?
Although the terminology of ‘unit fraction’ is not yet introduced, Year 1 pupils should:
- recognise, find and name a half as one of two equal parts of an object, shape or quantity;
- recognise, find and name a quarter as one of four equal parts of an object, shape or quantity.
In Year 2, pupils use fractions as ‘fractions of’ discrete (whole numbers) and continuous (any numerical value e.g. 3.6) quantities by solving problems using shapes, objects and quantities.
They connect unit fractions to:
- equal sharing and grouping;
- to numbers when they can be calculated;
- and to measures, finding fractions of lengths, quantities, sets of objects or shapes.
They also meet 3/4 as the first example of a non-unit fraction.
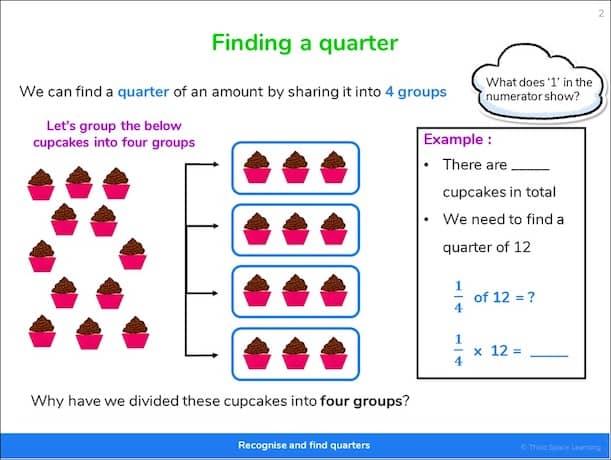
Year 3 pupils should:
- recognise, find and write fractions of a discrete set of objects: unit fractions and non-unit fractions with small denominators;
- recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators;
- compare and order unit fractions, and fractions with the same denominators;
- begin to understand unit and non-unit fractions as numbers on the number line, and deduce relations between them, such as size and equivalence;
- understand the relation between unit fractions as operators (fractions of), and division by integers;
- continue to recognise fractions in the context of parts of a whole, numbers, measurements, a shape, and unit fractions as a division of a quantity.
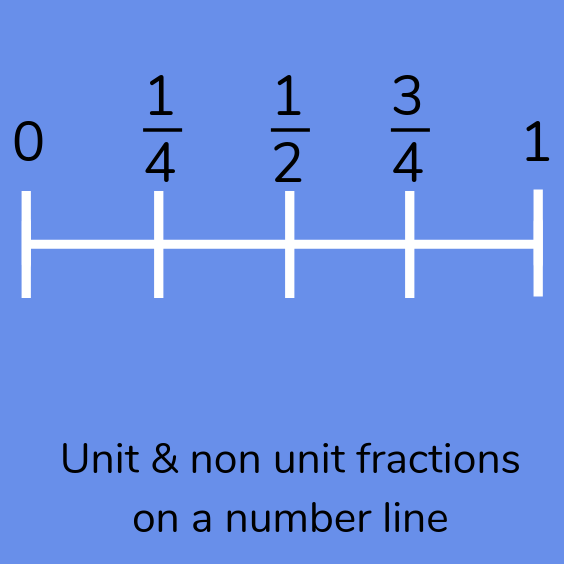
Unit fractions are then not mentioned in the curriculum until Year 6, where pupils use their understanding of the relationship between unit fractions and division to work backwards by multiplying a quantity that represents a unit fraction to find the whole quantity (for example, if 1/4 of a length is 36cm, then the whole length is 36 × 4 = 144cm).
Wondering about how to explain other key maths vocabulary to your children? Check out our Primary Maths Dictionary, or try these other terms related to unit fractions:
- What Are Equivalent Fractions?
- What Is BODMAS (and BIDMAS)?
- Properties of shapes
- What are 2D shapes?
- What are 3D shapes?
Unit fraction practice questions for primary school children
1) Write these numbers in order, starting with the smallest: 1/2, 1/4, 1/8, 1/5
2) Circle the biggest unit fraction: 1/6, 1/4, 1/3, 1/5
3) Shade in 1/5 of this shape (you can recreate this on a piece of paper):
4) Calculate 1/7 of 21.
Online 1-to-1 maths lessons trusted by schools and teachers
Every week Third Space Learning’s maths specialist tutors support thousands of primary school children with weekly online 1-to-1 lessons and maths interventions. Since 2013 we’ve helped over 150,000 children become more confident, able mathematicians. Learn more or request a personalised quote to speak to us about your needs and how we can help.
Primary school tuition targeted to the needs of each child and closely following the National Curriculum.
