Mental Maths Strategies Every Child Should Know From Year 2 To Year 6

When we think of mental maths strategies we are essentially thinking about those maths skills we can do in our heads, without using the formal written methods that we would use for longer questions and columnar methods. 

In this article we introduce you to some of the mental maths strategies you can teach your pupils to help develop their mental maths skills throughout primary.

What are mental maths strategies?

Mental maths strategies are accepted ways of working maths out in your head that help us take shortcuts and get to the correct answer in an efficient way.

Why are mental maths strategies important?

Mental maths strategies are the foundations for most of the areas of mathematics that use numbers. Without efficient mental strategies, children can often struggle to quickly and fluently calculate.

Mental strategies are also the foundation of any written or formal method in mathematics. Referring to it as mental maths does not mean you cannot write anything down at all, but any written work would be quick jottings to help remember through multi-step problems.

As children begin to use more formal methods, from around Year 4 onwards and as the numbers they are working with increase in value, mental maths skills are vital for ensuring fluency and accuracy in maths. 

In addition, there is the fact that the term ‘mental maths’ appears six times in the content domain breakdowns for the government’s KS2 Mathematics Test Framework; it’s one of the factors that the national tests are trying to assess.

Developing true fluency in mathematics

Effective mental strategies are important if children are to develop ‘true’ fluency

True fluency can be best defined as children being able to confidently use and apply their knowledge of number relationship, number facts and our number system in order to calculate and solve problems.

It is worth remembering that fluency in maths is not simply restricted to being able to recall known facts. More accurately, it is how children can use and apply these facts, including through a range of mental maths strategies, that are important.

“Low achievers are often low achievers not because they know less, but because they don’t use numbers flexibly.” – Jo Boaler

Third Space Learning’s one-to-one online tuition focuses heavily on building pupils’ confidence and fluency in maths. Tailored to each individual child’s needs, our weekly tutoring lessons aim to strengthen pupils’ understanding of number facts and how to apply them across a broad range of questions. 

Be careful not to mislabel mental maths skills

One important thing to remember when working to develop ‘true’ fluency is that accuracy is not the same as fluency.

For example, consider the following scenarios, which while accurate, may not necessarily be classed as fluent:

• A Year 2 child calculating 40 + 8 by counting in ones;
• A Year 4 child calculating 1003 – 998 using a formal written method;
• A Year 6 child calculates 41.79 + 25.3 + 25.7 – 41.79 by adding the first three numbers and then subtracting the fourth.

This extract from the research paper, ‘Developing Computational Fluency with Whole Numbers’ published in 2000 by S J Russell, remains one of the best explanations of fluency:

‘Fluency rests on a well-built mathematical foundation with three parts:

• an understanding of the meaning of the operations and their relationships to each other — for example, the inverse relationship between multiplication and division;
• the knowledge of a large repertoire of number relationships, including the addition and multiplication “facts” as well as other relationships, such as how 4 × 5 is related to 4 × 50;
• and a thorough understanding of the base ten number system, how numbers are structured in this system, and how the place value system of numbers behaves in different operations — for example, that 24 + 10 = 34 or 24 × 10 = 240’.

Rapid recall vs mental calculations with jottings

When we discuss mental calculations in maths at Key Stage 2, we need to be clear about the distinction between facts that children should be able to rapidly recall vs the types of calculations that children should be able to calculate mentally, sometimes with the support of jottings.

Retrieval practice and rapid recall of number facts is important because if children are able to recall number facts automatically, it allows them to free up their working memory when faced with more complex questions.

They are also able to more efficiently and accurately solve problems, reason and make connections if they are not having to repeatedly calculate the same ‘basic’ facts.

“In teaching procedural and factual knowledge, ensure the students get to automaticity. Explain to students that automaticity [with key number facts] is important because it frees their minds to think about concepts.” – Daniel Willingham – cognitive scientist, in ‘Is it true that some people just can’t do maths?’

The concept must be understood before introducing the strategy 

Before we can expect rapid recall and automaticity of number facts with our mental maths strategies, we need to teach the underlying maths concepts. For example, only when children have a secure conceptual understanding of number bonds to 10, should rapid recall be attempted. 

From this understanding of number bonds to 10, the strategy of partitioning can be used. For example,by Year 6 most children should be able to calculate 34 x 5 mentally (30 x 5 + 4 x 5) using partitioning and their knowledge of the distributive law supported by basic jottings.

Although pupils will be learning more and more maths facts which they can recall ‘by rote’ it is vital that they understand the concepts. Working with manipulatives can help with this, moving to virtual manipulatives on the interactive whiteboard when the numbers get too big to physically hold.

Using mental strategies in the SATs arithmetic test

Efficient mental calculation strategies are key to success in the KS2 SATs Paper 1: Arithmetic.

In the Arithmetic paper, over 80% of questions are designed to be able to be solved mentally, or through jottings.However, many children attempt the majority of the paper using formal written methods, which leads to them running out of time and not completing the paper. 

This is why, particularly in Year 6, we must explicitly teach pupils to use mental maths strategies alongside informal jottings when a full formal written method is inefficient, or too time consuming.

Assessing the mental maths strategies that your class is using

One really interesting way to check mental maths strategies is to present groups with different written versions of the same maths problems.

1. Present a single problem

If you present a problem, such as 64 + 17, in a sentence such as this, those children who are confident in their mental maths strategies, will work it out in their heads.

They will usually, even subconsciously if they are fluent, partition the numbers and work out 60 + 10 and then 4 + 7, or 60 + 17 then add the 4. Some will do 64 + 10 and then add the 7. 

Some may round the numbers, so say 64 + 20 using their number bonds to 20 knowledge and then minus 3. 

Some may again use their numbers bonds to work out 64 + 17 by adding 63 + 17 to make 80 and then add 1.

You would expect your class to give a range of answers regarding their method, but hopefully all are fluent and can find the correct answer without any more than a quick jot down of some numbers if adding multiple steps.

2. Create two versions of the same set of 10 questions

Now put together a sheet of 10 similar questions, with a range of addition and subtraction which you would expect your class to be able to do mentally. Create a second version of this which lays out the same questions, with the same exact numbers and same expected answer, in formal columnar method format. 

Give half the class the first sheet laid out as a number sentence and the other half the second version where the questions are laid out in a formal column method format. 

Do not tell groups that they have different sheets and hand them out to different tables so they do not see the other format of the same questions. Give them time to individually complete the questions and write down their answers. 

3. Ask children to share their methods

Take the first question and ask someone to volunteer to share their method. Then ask someone else to share, then someone else, and so on. Ensure you get a couple of examples from tables who have the horizontal layout of questions, and a couple of examples from the tables who have the vertical column layout. 

You will likely find that the groups who had a horizontal layout were much more likely to have just worked it out mentally, whereas the groups given the vertical layout will have spent time doing the column method to find and write down their answers, including every step, even though they could have easily completed those problems mentally. 

This activity is a great reminder that even when we see a formal calculation we should be using our mental maths strategies to speed up where we can. 

Building confidence in mental maths strategies

When any new maths concept is introduced – from addition through to percentages and decimals – children will benefit from being shown a physical representation of the numbers (using maths manipulatives) and operations before using pictorial representations (such as number lines or bar modelling) and then finally written methods using the symbols of number and operation. 

Read more: Concrete Pictorial Abstract Method

Along the way there will need to be lots of repetition and practice recalling facts mentally. As children get older, into Key Stage 2, the move from physical to written will hopefully get quicker for new concepts as they are building on a solid foundation. 

Different children may be able to move to mental strategies at varying points of each unit. Some may jump from physical to mental if they grasp the concept quickly and have a sound understanding already. 

Others may not be able to reach fluency of recall and application until they have had a lot of practice with writing their answers down and building confidence in those new number facts and strategies. 

You may also need to unpick any misconceptions through those stages too, and this may involve going ‘backwards’ to the physical. It is good practice to always have manipulatives available during independent tasks even in Year 6 and for all abilities. Sometimes a quick comparison using some Base 10 or Cuisenaire rods can help a child to ‘fix’ that strategy in their head. 

It is also important not to teach children to do ‘tricks’ in maths such as “add a zero” when multiplying by ten as this can cause issues in later years with their understanding of place value. You would hope, however, that children spot such patterns in their answers and this should lead to discussion and comparison as well as presenting opportunities for children to test their theory, where they have spotted a possible pattern. Even if you know it is wrong/right, they will gain from the chance to test and apply that assumption.

Read more: Maths tricks to avoid 

The mental maths strategies children should know by the end of Year 6

By KS2 there are some specific mental maths calculations that will help children immeasurably when working in both written work and mental work, arithmetic and reasoning. They actually form a progression starting from Year 3, so it is important that the groundwork has already been done in KS1 to enable children to carry out the calculations mentally.

These skills are therefore best looked at as a progression, rather than a set of year group expectations.

How to improve mental maths year by year

As well as building on children’s range of mental calculations as they progress through KS2, make sure they are also secure in their number facts each year.

For more specific advice on teaching mental maths and number facts within the national curriculum follow the links below:

• Mental Maths Year 2
• Mental Maths Year 3
• Mental Maths Year 4
• Mental Maths Year 5
• Mental Maths Year 6 

How to develop the mental maths strategies needed for addition and subtraction

In Key Stage 1 children will learn basic number facts including addition and subtraction. This will include number bonds to 20 by the time they finish Year 2. They will do a lot of work with physical objects and role play, so it is good practice in these years to not just practise maths skills during the maths lessons (where you will be covering the National Curriculum content more formalling in a progression) but also to make opportunities for questioning outside of these lessons. 

Ask children to count up how many pupils are absent today, counting the pencils on each table to see if they have enough (or too many or too few) and reinforce vocabulary from maths lessons.

Once children have grasped the concept of addition facts and subtraction facts, and that they are inverse operations (they may not know that specific word yet though) they will begin to solidify their rapid recall of number bonds and apply them to their work.

It is never too early to introduce different strategies to work out their calculations either, so long as the base understanding is correct. Asking them if there is another way they could have found the answer is a question which can be asked in formal lessons, in role play or in sports. 

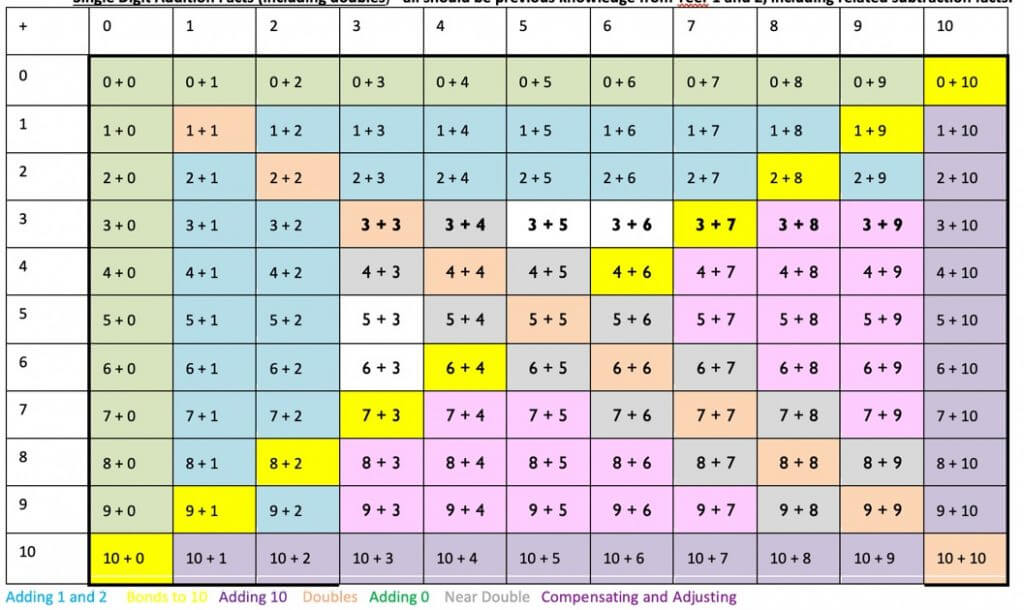
Mental addition strategies and mental subtraction strategies at KS2 

Counting forward and backwards

Counting forwards and backwards is first encountered in KS1, beginning at one and counting on in ones.

Pupils’ sense of number is extended by beginning at different numbers and counting forwards and backwards in steps, not only of ones, but also of twos, fives, tens, hundreds, tenths and so on.

Progression in counting forwards and backwards

These are the ways you can help your class to progress with counting forwards and backwards:

1. Counting on or back in tens from any number. E.g. working out 27 + 60= ? by counting on in tens from 27
2. Counting on or back in fives from any multiple of 5– e.g. 35+15=? by counting on in steps of 5 from 35.
3. Counting on or back in hundreds from any number e.g. 570 + 300= ? by counting on in hundreds from 570.
4. Counting on or back in tenths and/or hundredths- e.g. 3.2 + 0.6 = ? by counting on in tenths. 1.7 + 0.55=? by counting on in tenths and hundredths.

Partitioning for addition and subtraction

Partitioning strategies teach children how to break up larger numbers into smaller ones.

It is important that children are aware that numbers can be partitioned – both along the place value boundaries (canonically) and in other ways (non-canonically).

They can then use their partitioning to help them calculate addition and subtraction calculations. This can be extended as children progress through KS2.

Progression in partitioning

These are the ways you can help your class to progress with partitioning:

1. Calculations with whole numbers which do not involve crossing place value boundaries. E.g. 23 + 45= ? by 40 + 5 +20 + 3 or 40 + 23 + 5
2. Calculations with whole numbers which involves crossing place value boundaries. E.g. 49 – 32= ? by 49 – 9 – 23 or 57 + 34=? by 57 + 3 + 31
3. Calculations with decimal numbers which do not involve crossing place value boundaries 5.6 + 3.7= ? by 5.6 + 3 +0.7  or 540 + 380= ? by 540 + 300 + 80 or 540 + 360 + 20
4. Calculations with decimal numbers which involve crossing place value boundaries. E.g. 1.4 + 1.7= ? by 1.4 + 0.6 + 1.1 and 0.8 + 0.35= ? by 0.8 + 0.2 + 0.15

Compensating and adjusting

Compensation involves adding more than you need and then subtracting the extra.

This strategy is useful for adding numbers that are close to a multiple of 10, such as numbers that end in 1 or 2, or 8 or 9.

The number to be added is rounded to a multiple of 10 plus or minus a small number.

For example, adding 9 is carried out by adding 10, then subtracting 1. A similar strategy works for adding decimals that are close to whole numbers.

These are the ways you can help your class to progress with compensating and adjusting:

1. Compensating and adjusting to 10. E.g. 34 + 9=? by 34 + 10 – 1 or 34 – 11= ? by 34 – 100 – 1 = ?
2. Compensating and adjusting multiples of 10. E.g. 38 + 68= ? by 38 + 70 – 2 or 45 – 29 = 45 – 30 + 1
3. Compensating and adjusting multiples of 10 or 100. E.g. 138 + 69= ? by 138 + 70 – 1 or 299 – 48 = 300 – 48 – 1
4. Compensating and adjusting multiples with decimals. E.g 2 ½ + 1 ¾ by 2½ + 2 – ¼  or 5.7 + 3.9 by 5.7 + 4.0 – 0.1

Calculating using near doubles

When children have an automatic recall of basic double facts, they can use this information when adding two numbers that are very close to each other.

These are the ways you can help your class to progress with near doubles:

1. Near doubles to numbers under 20. E.g. 18 + 16 is double 18 and subtract 2 or double 16 and add 2.
2. Near doubles to multiples of 10. E.g. 60 + 70 is double 60 and add 10 or double 70 and subtract 10 or 75 + 76 is double 76 and subtract 1 or double 75 and add 1.
3. Decimal near doubles to whole numbers. E.g. 2.5 + 2.6 is double 2.5 add 0.1 or double 2.6 subtract 0.1.

How to develop the mental maths strategies needed for multiplication and division 

As pupils move through primary school they will learn the times tables ready for the statutory test, administered in Year 4. They will need fluency in multiplication facts to enable them to recall these fast enough for the test. It is again vital that they understand the concept of multiplication rather than simply parroting the facts, rote style. Though, practice is crucial as daily recall of known facts is vital to stop new facts pushing out the old where they are not fully embedded. 

Children start multiplication understanding with doubling and halving in Key Stage 1. This introduces the concepts of both multiplication and division and they should start noticing the patterns of these and apply this to maths questions. In Year 2 they will also learn times tables for 5 and 10 and this starts with counting forwards and backwards in 5s and 10s, which they should also be doing from any given number not just zero.

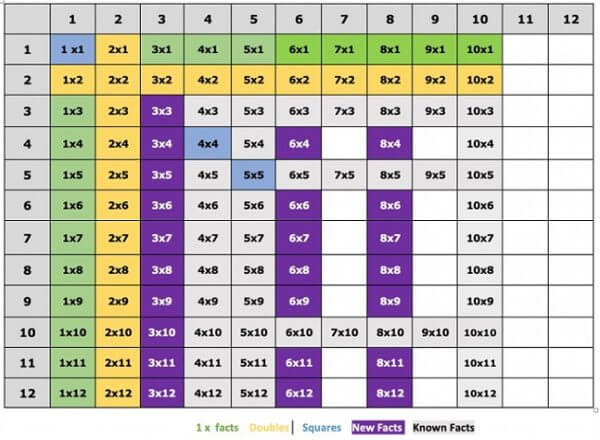
In Year 3 the 3, 4, and 8 times tables are added. And then in Year 4 the 7, 9, 11 and 12 times tables. They should also be applying these to word problems and multi-step problems as confidence increases, to ensure they are able to apply number facts rather than simply repeat them. These mental arithmetic skills, and the fluency of them, will be vital in test situations. By the time they go to secondary school, they should have a very firm grasp of the number system along with known facts and patterns.

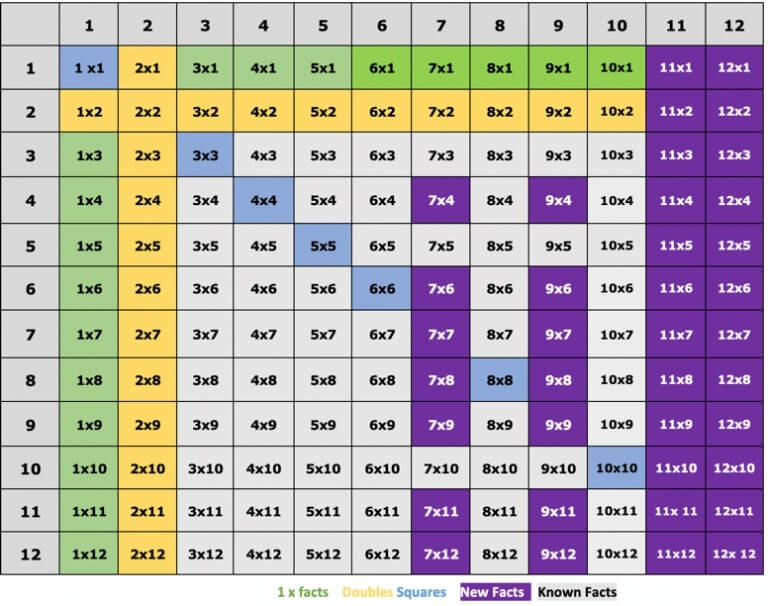
Place value multiplication strategies

Children should be able to build upon their rapid recall of 1-12 x multiplication and division facts, and multiplication and division facts for multiples of 10 and 100 to calculate an increasing range of multiplication questions mentally.

These are the ways you can help your class to progress with place value:

1. Multiply a 2-digit number by a single-digit number by partitioning. E.g. 26 x 3 = 20 x 3 + 6 x 3
2. Multiply a decimal number with up to 2 decimal places by a single digit by partitioning. E.g. 3.42 x 4 = 3 x 4 + 0.4 x 4 + 0.02 x 4

Doubling and halving strategies

Children should be able to recognise halving as the inverse of doubling and be able to rapidly calculate doubles and halves of numbers.

Some double and half facts are rapid recall rather than ones that children should need to calculate each time, and these are covered in the lists above.

These are the ways you can help your class to progress with doubling and halving:

1. Find the doubles and halves of any two-digit number and any multiple of 10 or 100. E.g. half 680 or double 73
2. Multiply and divide by 4 by doubling/halving twice and 8 by doubling/halving again. E.g. 34 x 4 = 34 x 2 x 2.
3. Find the doubles and halves of any number up to 10,000 by partitioning. E.g. half of 32,202 by halving 3,000, 2000, 200 and 2.
4. Multiply by 50 by multiplying by 100 and halving. E.g. 8 x 50= 8 x 100 divided by 2
5. Divide a multiple of 25 by 25 dividing by 100 then multiplying by 4 (by doubling and doubling again). E.g. 350 ÷ 25 = 350 ÷ 100 x 2 x2
6. Divide a multiple of 50 by 50 by dividing by 100 then doubling. E.g. 450 ÷ 50= 450 ÷ 10 x 2
7. Double and half decimal number with up to one decimal place by portioning. E.g. half of 8.4 by halving 8 and halving 0.4

Mental calculation strategies for fractions, decimals and percentages

As they progress through KS1 and 2, children should develop their understanding of fractions, decimals and percentages and how they are related to division.

By Year 6, they should therefore be able to use their rapid recall of multiplication and division facts to calculate some questions involving fractions, decimals and percentages, mentally.

These are the ways you can help your class to progress with fractions, decimals and percentages:

1. Mentally find fractions of numbers in the 2,3,4,5 and 10 times table using known multiplication and division facts. E.g. 3/5 of 45 by 45 ÷ 5 x 3.
2. Recall percentage equivalents to ½, 1/3, ⅕, ⅙, 1/10 and 1/100. E.g. ¼ = 25%
3. Find 10% or multiples of 10% of whole numbers and quantities. E.g. 30% of 50 by 50 ÷ 10 x 3
4. Mentally find 50% by halving and 25% by dividing by 4 or 2 of numbers and quantities. E.g. 25% of 150 by 150 ÷ 4

Mental maths percentages hack 

The tweet below is something that you may have seen going around twitter in early 2019, but it represents a useful strategy to help work out tricky percentages.

Top Mental Maths Tips: How You Can Teach Mental Maths Strategies

We’ve dealt with the ‘what’ in significant detail, but how do we actually go about teaching mental maths strategies? Here is a summary of our top tips:

1. Teach mental maths strategies and mental calculation techniques, don’t just rely on children ‘picking them up’. It is important that lesson time is devoted to teaching strategies conceptually and supporting children to make connections between their known facts and mental calculations. This is best achieved through modelling and the use of manipulatives etc.
2. Engage children in discussion. Children should be encouraged to discuss their mental strategies with each other and as a class, and adults in the classroom should join in this discussion. Children will see and approach calculations mentally in different (equally as valid) ways and through sharing these they expose each other to different ways of thinking about and ‘seeing’ a calculation.
3. Provide regular mental maths practice. Children should have regular mental maths practice that focuses on mental calculation strategies. Alongside teaching the strategies in the main maths lesson, schools where children have a high level of competency and fluency in mental strategies often devote 15-20 minutes a day to the practise and development of mental strategies and rapid recall outside of the main maths lesson.
4. Don’t think that timed testing is the only way to achieve rapid recall. Timed testing has been shown by many research studies to be one of the least effective ways of developing rapid recall. Instead, ensure children have plenty of opportunities to use, apply and recall the facts that you want them to be able to recall rapidly.
5. Play games and create opportunities for meaningful activities. If the activities are fun and meaningful children will be supported in developing number sense and fluency in an increasing range of calculations.
6. Ensure ‘basic’ number facts are practised. It’s important that you do not neglect ‘basic’ number facts, for example, number bonds within 10, 20 and 100 and the 1-12x multiplication table. Often facts such as number bonds are only practised at KS1, but it is vital that these are practised and children are encouraged to use these facts in their mental calculations. Remember, if you don’t provide the opportunity for them to use it, they will lose it!

Mental maths games

Mental maths games are a great way to develop good mental maths skills. Here are some to get you started. 25 fun maths games to do at school or at home, also KS2 maths games, KS1 maths games and KS3 maths games for all maths topics and a set of 35 times tables games you’ll want to bookmark whichever year group you teach!

The best resource for developing pupils mental maths strategies in KS1 and KS2

Our Fluent in Five resource has been designed specifically to help develop the skills needed for success in the maths SATs Arithmetic paper, with a key focus of the resource being the identification of questions which would be more efficiently solved with a mental or written method.

For Years 5 and Year 6 mental maths worksheets are included as part of the Fluent in Five resource. For Years 1 to 4, the mental maths questions are all on slides only.

Fluent in Five is already used in thousands of schools across the UK, so why not try the first 6 weeks for free here: Fluent in Five for Year 1, 2, 3, 4, 5, 6

Third Space Learning’s Ultimate Mental Maths Pack also provides over 150 mental maths questions for pupils to practice their mental maths skills. 

Read more:

• How To Teach Times Tables So Pupils Learn Instant Recall
• What Is Fluency In Maths?
• The 20 KS2 Maths Strategies That Guarantee Progress
• Ultimate Guide To Maths Problem Solving

References:

Russell, Susan Jo (2007). Developing  Computational Fluency with Whole Numbers in the Elementary Grades