5 Maths Tricks Or Bad Habits We Should No Longer Be Teaching Primary School Pupils in KS2
As teachers we’re all looking for shortcuts and easy maths tricks to teach our pupils but is this really the best way to help our primary school pupils in KS1 and KS2?
Here’s an example…
When you multiply by ten you just add a zero.
Does this make you cringe? It should do as it simply isn’t true. And we know why, don’t we? If you add a zero you’re adding nothing, therefore the number doesn’t change.
Try telling that to a child who has worked it out for themselves without you ever having to utter the forbidden phrase.
As primary teachers, following the recommendations from the EEF’s report on improving mathematics at KS2 we need to model good conceptual understanding in all our maths lessons, rather than relying on easy maths tricks that work but don’t help children to have an understanding of the ‘why’ and the ‘how’.
Here are the 5 most common bad habits I’ve identified in my role as a primary maths subject leader; these are the easy maths tricks teachers should no longer be using and some much clearer ways to explain the maths instead.
Maths trick 1: Using a written calculation when a mental one would do
The problem: Taking the long way round
When it comes to arithmetic skills, true fluency and understanding means selecting the appropriate method of calculation.
Often weaker mathematicians who have learned to follow the steps of a written calculation resort to using one wherever they see the + symbol. Even when there’s clearly a more efficient way of solving the problem.
Some teachers even encourage this behaviour because ‘at least they get the right answer’, but really, this does not support their conceptual thinking further down the line.
Anyone who has marked a SATs arithmetic paper will have seen children arriving at an answer to 987 + 100 = using column method. It’s basic place value and certainly something that should be done mentally, with very little thought.
Try this: Children explain the method they’re using
Set an activity where all children simply have to select a method and explain why they’d use it. You can do this verbally, or in writing. Don’t even worry about solving the problems themselves. The focus here should only be on selecting a method.
For example, given a question 50 x 70, you’d hope pupils would not use the formal written method of multiplication. Instead they’d use their times tables and place value knowledge to derive the answer.
When you conduct this activity, make sure to include questions where children would have to use a range of methods, written and mental.
FREE Fluent in Five Arithmetic Pack: Years 3 to 6 [Weeks 1 to 6]
Daily arithmetic questions to build number fluency in pupils; focus on choosing between written & mental strategies. Progression document builds towards speed and stamina in KS2 SATs
Download Free Now!Maths trick 2: Teaching written calculations without concrete representations
The problem: Understanding borrowing
A maths graduate and teacher said this to me recently: “For years, I had no idea why I crossed out a number and put a one next to the other number.”
As a child he had not been taught why or what he was ‘borrowing’ from the next column in his subtraction written method. Nor had he been helped to understand why he had to ‘carry’ the tens when completing a written calculation for addition.
I am willing to bet good money that this lack of understanding is rife.
Try this: Use physical representation
The key here is to model understanding. Key Stage 1 teachers often do this through manipulatives or other equipment, but we often forget to use these tools for Key Stage 2.
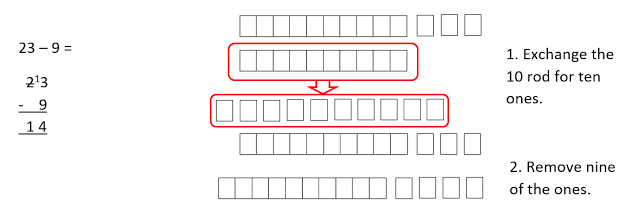
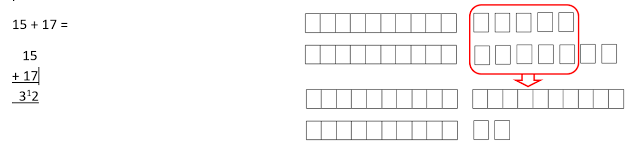
Give children a physical representation of the exchange that takes place when in addition the tens are crossed. Or when in column subtraction the digit being taken away is smaller than the first digit.
You can use items such as bundles of 10 straws, Base 10/Dienes, multilink cubes in sticks of 10. Really anything that can be put in and out of groups of ten! Model the exchange that occurs in the written processes.
Maths trick 3: De-contextualising negative numbers
The problem: Negative numbers seem too abstract
With many other areas of arithmetic and calculation, we tend to strip questions of any context (for example the SATs arithmetic paper). However, negative numbers are definitely a concept which need to be contextualised at all times.
Children already have very little concept of negative numbers in real life (they don’t have bank balances for a start) so, as an abstract concept, it is way outside of their natural understanding.
Try this: Use a vertical number line
Use a number line, a horizontal number line is OK, but a vertical one is even better. If you can then put that number line into a context the children are more likely to understand, then you’ll be onto a winner.
The best examples I’ve used are where children imagine, and eventually draw, a number line which is actually a building with floors above ground and floors below ground. The children can see, for example, that the first floor below ground floor (zero) is -1 meaning one below.
This ‘number line’ will is also great for setting and solving addition and subtraction problems: ‘If I get in the lift at floor 5 and go down 7 floors, which floor will I arrive at?
Similar contexts such as above and below the sea will also work. The fact that thermometers too are usually encountered as a vertical number line supports this idea.
Maths trick 4: Rounding numbers
The problem: Rounding to 10,000 is much harder than rouning to 2 digits
Children are usually taught to round in Key Stage 1 with a number line. We often then strip them of this pictorial privilege in Key Stage 2, making it a much more abstract process. For many, this happens before they truly understand how it all works.
Children are expected to work with larger and larger numbers and round to different amounts as the curriculum progresses.
Given this, we shouldn’t assume that because they could round to the nearest 10 in Year 2 that they can round a 7 digit number to the nearest 10,000 in Year 6.
Try this: Go back to the number line!
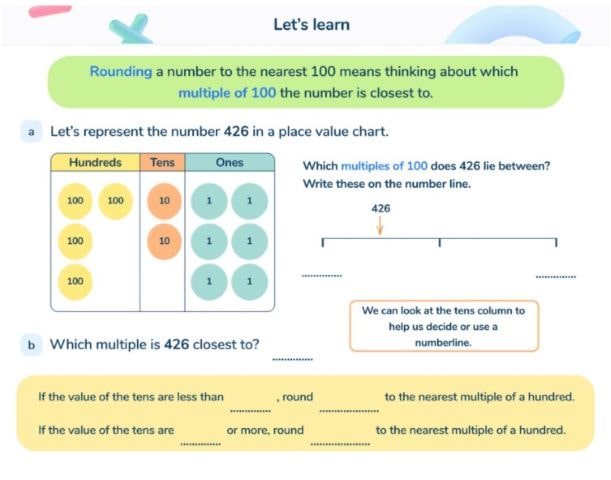
Number lines to the rescue again! Use number lines throughout school, regardless of age or ability. When rounding to ten (using their place value knowledge) children will first need to find the preceding and following multiples of ten. These will be placed at either end of the number line.
Then, they should mark halfway (a multiple of 5) and then place the number they are rounding in the relevant place on the line. They will now be able to see which multiple of ten it is closest to.
It also might be worth making the number line 10cm long so that they can accurately place the numbers. This process can be repeated for rounding to 100s, 1000s and so on.
Maths trick 5: Codifying mathematical processes
The problem: Statements which don’t embed conceptual understanding
“You divide by the bottom and times by the top!” But why? Sayings like this are useful because they work, but they don’t lead to a conceptual understanding of the Maths at work.
This is especially the case if you put these sorts of statements into knowledge organisers; the statement is internalised rather than the concept.
As teachers, we often think we have competent mathematicians on our hands because they can
- find a fraction of an amount
- divide a fraction by another fraction “Keep. Change. Flip” (this isn’t even on the primary curriculum but many seem to touch on it)
- multiply two fractions together “Multiply the denominators together, multiply the numerators together.”
- add two fractions together “The bottom number doesn’t change.”
We are fooling ourselves by thinking that. We’re doing the children a disservice. Without a good conceptual understanding of what happens in any one of those processes children will struggle to apply their maxims to other problems.
Try this: Use a concrete or pictorial representation of anything that has an easy-to-remember rule
Question: What is 3/7 of 28?
Ask children to use the squares in their book to create a grid containing 28 squares (represented below by rectangles):
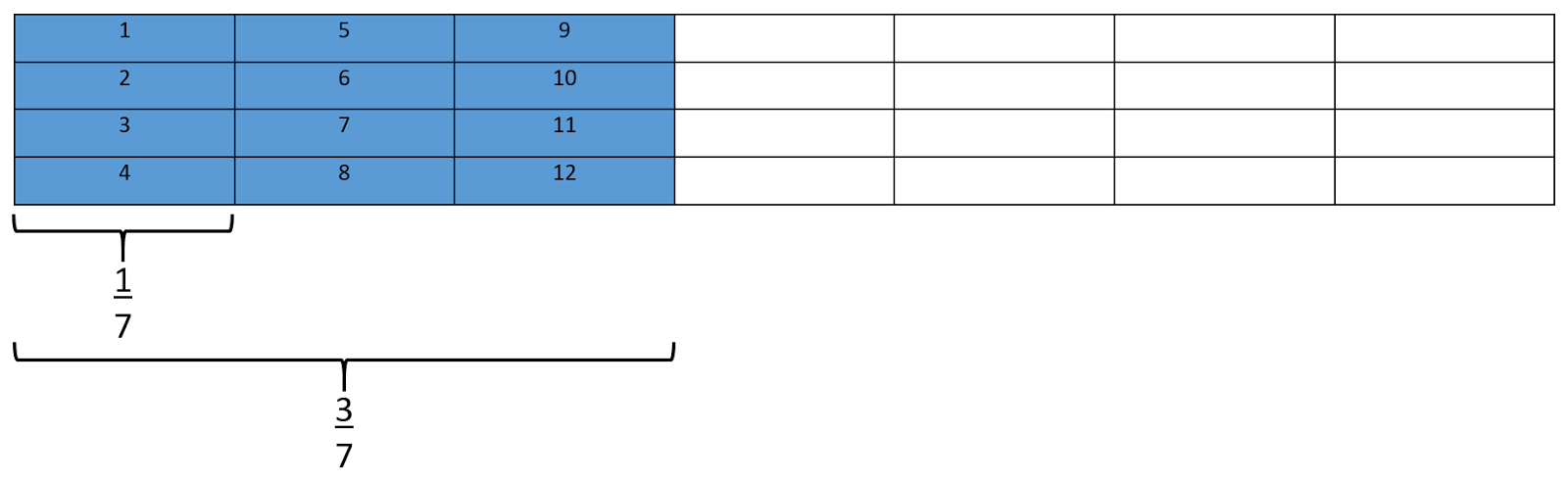
They should do this using their times table knowledge. Knowing that in this example 28 divides exactly by 7, meaning that they need to draw a 4 by 7 grid (because 4 x 7 = 28). In the diagram below, each column represents one seventh of the total (28), so children can see then that one seventh is 4.
To find three sevenths they could shade three of the columns and count up the total number of squares shaded. Here’s another:
Statement: 2/3 x 1/4 = _____ is the same as 2/3 of 1/4 = _____
First up, children will need some background knowledge here, and the following two concepts will need to be modelled before reaching this level of question:
- When you multiply a number by a fraction, you are actually just finding that fraction of that number.
- When you multiply a positive number by less than a whole, the resulting answer will be smaller than the number you started with.
Ask children to draw a rectangle which is split into quarters. This is a whole. Then ask them to shade a quarter to represent the quarter in the question, like below:

Next, ask children to split the whole shape into thirds, this time with the dividing lines going horizontally. They should then shade in two thirds of the part already shaded in, like below:

Here, some children do get confused as to which parts to shade so lots of modelling and discussion of this technique is necessary (but worthwhile).
Children should then be able to see that the whole shape has been split into 12 parts, which becomes the denominator and that two thirds of one quarter is represented by two of those 12 parts. This can be then made into the fraction 2/12 which can be simplified to 1/6.
Obviously, this example is a Year 6 skill and a good understanding of the Maths behind it relies on years of quality modelling of other simpler fractions problems.
Question: 2/3 ÷ 1/4 =
For this question, children will need some squared paper to ensure accuracy. They will then need to draw a rectangle the length of the denominators multiplied. This is because to solve this we need to find a common multiple so that the two wholes are equal, accurate and comparable.
Children also need to understand that this question is asking ‘How many quarters are there in two thirds?’
On the top we have split the whole into thirds and below that we have split the whole into quarters, as below:
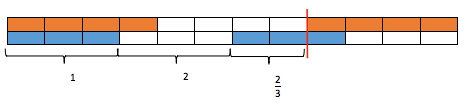
When we then partition off the two thirds (because that’s what the question is about, not a whole) we can see how many of the quarters are in (or equal to) the two thirds. In this case there are two full quarters and then two thirds of a quarter left.
So the answer to ‘How many quarters are there in two thirds?’ is that there are 2 and 2/3 quarters in two thirds.
Try this for dividing a fraction by a whole number
A similar model can obviously be used for dividing a fraction by a whole number, like this question:
Question: 1/2 ÷ 3 = _____
Here, the top bar is split into halves. Each half is then split into three. This shows that in the original whole there are six parts, so sixths. When you split a half of the whole into three parts it is a sixth of the whole. As below:

The complexity of the maths behind problems like these might make us want use maths tricks to get pupils successfully answering faster. But really, these maths tricks are just bad habits which support no real maths understanding. For pupils to truly succeed and become great mathematicians, they have to understand the concepts that underpin a problem.
Read more
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

![FREE Fluent in Five Arithmetic Pack: Years 3 to 6 [Weeks 1 to 6]](https://thirdspacelearning.com/wp-content/uploads/2018/03/Fluent-in-Five-Weeks-1-6-1.png)


