Teaching Ratio And Proportion KS2: A Guide For Year 6 Teachers
Ratio and proportion in KS2 maths appear only in Year 6, but just as with other advanced topics such as algebra, it is essential pupils can approach it with confidence in their Key Stage 2 maths SATS. This blog will help you ensure that your pupils can do just that.
The National Curriculum of 2014 brought with it a dedicated section for Ratio and Proportion into the program of study at Year 6 only.
While some of the objectives within the National Curriculum may seem convoluted (and perhaps to some fear-inducing) there is no need to worry, as students will have come across many of the ideas in previous years without it being made explicit.
What is ratio and proportion?
Ratio describes how the amounts of two things compare to one another, while proportion describes an amount of something.
Kieran Mackle in his book Tackling Misconceptions in Primary Mathematics (2017) writes that ‘ratio describes the quantitive relationship between two amounts and essentially shows the number of times one value contains or is contained within the other while proportion refers to a part, share, or number considered in comparative relation to a whole.’ (P.93)
The objectives that need to be met specifically reference the use of prior knowledge of shape, multiplication and division facts, percentages, fractions and multiples. Given the relationship between ratio and proportion and these other curriculum areas, it makes sense to ensure that students are fluent in these areas before teaching ratio and proportion.
from Third Space Learning’s online maths interventions.
Remember, getting the prerequisite knowledge for a topic to a degree of fluency (when you no longer have to give attention) will aid the learning of the new material that is being taught as it frees up vital working memory with which students can think mathematically about the new material.
Looking to get your pupils caught up in this prerequisite knowledge? Check out the other blogs in our series on KS2 maths, including teaching place value, fractions KS2, and teaching decimals.
As ever, the teacher who possesses excellent pedagogical content knowledge will be able to demonstrate the conceptual mathematics behind ratio and proportion and, with the use of careful language and manipulatives, demonstrate those underlying structures to the pupils and relate it to previous learning.
An excellent manipulative to demonstrate ratio and proportion would be Cuisenaire rods and as pictorial representation, the bar model.
Independent Recap Ratio and Proportion Worksheets
Download for FREE this pack of four ratio and proportion worksheets for Year 6 pupils. Intended to provide opportunities for pupils to independently practise what they've been learning.
Download Free Now!Teaching Ratio and Proportion in KS2
When beginning this unit, getting the language and vocabulary of ratio correct is absolutely key to being successful in this unit. Children need a clear understanding of what the ratio symbol means, ideally this begins to be implemented before the students have even seen the symbol.
Using the phrase ‘__ for every __’ consistently is a good way to build up this understanding. As this series may have taught you, I advocate the use of manipulatives in the classroom to support conceptual understanding all the way up through to Year 6 and beyond and the using representations that the students are familiar with will help this conceptual understanding come about even faster.

Unlimited primary maths tutoring with Skye, the voice-based AI maths tutor.
Built on the same principles, pedagogy and curriculum as our traditional tutoring but with more flexibility, reach and lower cost.
Join the schools already helping hundreds of primary pupils nationwide with Skye’s one to one maths tutoring
Watch Skye in actionRatio and Proportion Year 6
In the National Curriculum for maths in England, for each area of maths outlined, there is both a statutory requirement and a non-statutory requirement. The statutory requirements in KS2 maths are as follows:
- Solve problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts
- Solve problems involving the calculation of percentages [for example, of measures and such as 15% of 360] and the use of percentages for comparison
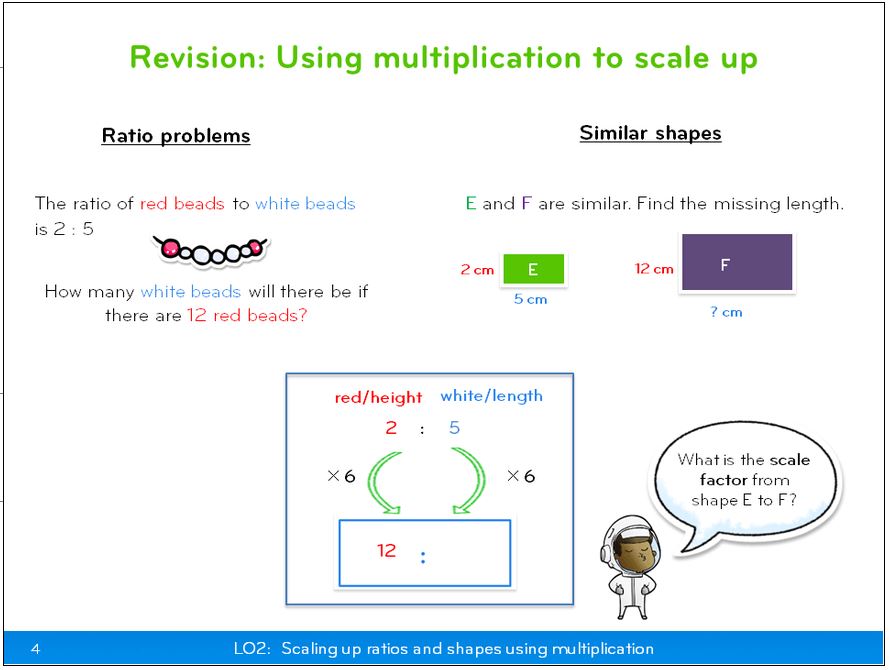
- solve problems involving similar shapes where the scale factor is known or can be found
- solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
Non-statutory notes and guidance suggest:
- Pupils recognise proportionality in contexts when the relations between quantities are in the same ratio (for example, similar shapes and recipes).
- Pupils link percentages or 360° to calculating angles of pie charts.
- Pupils should consolidate their understanding of ratio when comparing quantities, sizes and scale drawings by solving a variety of problems. They might use the notation a:b to record their work.
- Pupils solve problems involving unequal quantities, for example, ’for every egg you need 3 spoonfuls of flour’, ‘3/5 of the class are boys’. These problems are the foundation for later formal approaches to ratio and proportion.
Ratio and Proportion Lessons Year 6
An ideal way to introduce ratio in a meaningful, and relevant context that students would have prior knowledge of would be creating squash where they experiment with different ratios of squash to water. Making mocktails is also another popular activity.
Though I feel that it is best used once students have a greater understanding of ratio as mocktails can introduce three values into the ratio (1:4:6). Beginning with squash allows for a ratio that contains only two values which is a logical first step.
That said, we need to take heed of the lessons from cognitive science and episodic and semantic memory. Learning in this way can lead to strong episodic memory – where the students will talk about that time they made squash during a maths lesson but the actual conceptual understanding of ratio will not be remembered as students were thinking about the ratio of squash to water.
Therefore, before allowing students to take part in such an activity, it is important that they are first asked to think carefully about ratio. Cuisenaire rods and other teaching resources allow the teacher to guide a students understanding of ratio in a concrete way which should then be supplemented by images where it is possible to find different ratios. For example:

Using the Cuisenaire rods allows for these ratios to be made. When explaining the relationship of the rods and how they relate to ratio, using language like ‘1 for every 2’ consistently will be key (note that on most cuisenaire rods the values are not shown, these are there simply for demonstrative purposes).
Creating contexts for these ratios are also beneficial. If you look at the second ratio as demonstrated by the rods, you could put this into the context of fruit and say for every two red apples there are 3 green apples etc.
The last example of the rods is an important one as the ratio is still 5 for every 8 but this is simply repeated. This lays some foundational thinking for equivalent ratios; pupils can learn that ratio has a lowest term (simplest form) and that 10:16 = 5:8. I would not make this explicit in the first lesson however.
Giving students the opportunity to experience thinking about ratio by manipulating the Cuisenaire rods is also important so you may verbally want to give a ratio and get the students to demonstrate this using the rods.
Once you are happy that students have some conceptual understanding of ratio, you could move them onto the squash problem. To ensure that they remain thinking about the ratio, you could get them to draw each ratio of water to squash they try to until they have found their preferred taste.
As it would be down to personal taste, there would be no set answer but the picture below would be an example of how a student could set this out. You would need to make sure they are consistent with what each part is e.g. the bottom rod always represents the water and the top rod always represents the squash.
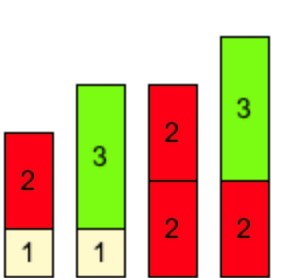
You would also have to ensure consistency of what each part of the ratio represents. I have found each part representing 50ml has been effective in the past.
Getting students to generalise and identifying relationships are an important part of a mathematical education and this activity allows for this. As a teacher, I would be asking what they notice about the strength of the drink and how this varies depending on the ratio of water to squash.
Ratio and Proportion Problems Year 6
Nutty Mixture from Nrich provides a good ratio word problem that students would be expected to solve by the end of the unit on ratio. They can use manipulatives to help them solve or, if feeling more confident, a bar model.
Rachel has a bag of nuts.
For every cashew nut in the bag, there are two peanuts.
There are 8 cashews in Rachel’s bag. How may peanuts are there?
Marianne also has a bag of nuts.
In Marianne’s bag, for every two cashew nuts, there are three peanuts.
Marianne’s bag contains 12 peanuts in total. How many cashews are in her bag?
Rachel and Marianne decide to mix their bags of nuts together.
What is the ratio of cashew nuts to peanuts in the mix?
The above can be solved by creating a train using the Cuisenaire rods and creating additional markings to distinguish the same rod being used for a different type of nut.
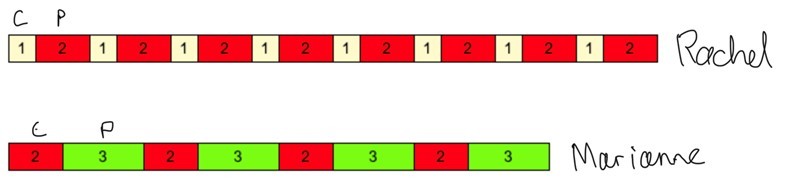
depicting ratio problems.
From this representation you can see that for the 8 cashew nuts, there would be 16 peanuts in Rachel’s bag. In Marianne’s bag, there would be 8 cashew nuts in total. To solve the final part of the question, you would need to bring one proportion of Rachel’s and one proportion of Marianne’s together and combine the cashew and peanut quantities together.
Students could then experiment which two rods are equivalent to the amount of cashews and which rod is equivalent to the amount of peanuts. The ratio of the combined bag is 4:7.
See more: 15 ratio and proportion questions
Ratio and Proportion: Reasoning and Problem Solving Year 6
It is important that we do not just use one representation with students as they will find it difficult to transfer their learning into new contexts; use multiple representations.
This ratio problem uses different colour counters and a series of statements that the students need to prove are either true of false. The answers are in brackets after the statement.
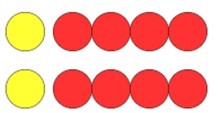
- For every yellow counter there are 8 red counters (False)
- For every 4 red counters there is 1 yellow counter (True)
- For every 3 yellow counters there would be 12 red counters (True)
- For every 16 counters, 4 would be yellow and 12 would be red (False)
- For every 20 counters, 4 would be yellow and 16 would be red (True)
Encouraging students to draw or use counters for each statement that require it should be encouraged as it demonstrates to you what it is they are thinking and will allow you to pick up any misconceptions in their understanding and correct them immediately.
Ratio and proportion is a complex topic, and one introduced late on in KS2. Hopefully this post has given you some good ideas to help your pupils approach it with confidence.
For guidance on other KS2 subjects, check out the rest of the series:
- Teaching Decimals KS2
- Teaching Place Value KS2
- Teaching Fractions KS2
- Teaching Percentages KS2
- Teaching Statistics KS2
- Teaching Multiplication KS2
- Teaching Division KS2
- Teaching Addition and Subtraction KS2
- Teaching Geometry – Position, Direction and Coordinates KS2
- Teaching Properties of Shapes KS2
You may also be interested in:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about primary maths tutoring for your school.