Ratio Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included
Ratio questions appear throughout KS3 and KS4 building on what students have learnt in primary school. Here we provide a range of ratio questions and practice problems of varying complexity to use with your own students in class or as inspiration for creating your own.
Free GCSE maths revision resources for schools
As part of the Third Space Learning offer to schools, the personalised online GCSE maths tuition can be supplemented by hundreds of free GCSE maths revision resources from the secondary maths resources library including:
What is ratio?
Ratio is used to compare the size of different parts of a whole. For example, in a whole class of 30 students there are 10 girls and 20 boys. The ratio of girls:boys is 10:20 or 1:2. For every one girl there are two boys.
Uses of ratio
You might see ratios written on maps to show the scale of the map or telling you the currency exchange rate if you are going on holiday.
Ratio will be seen as a topic in its own right as well as appearing within other topics. An example of this might be the area of two shapes being in a given ratio or the angles of a shape being in a given ratio.
visual representations are a really useful way in.
Ratio in KS3 and KS4
In KS3, ratio questions will involve writing and simplifying ratios, using equivalent ratios, dividing quantities into a given ratio and will begin to look at solving problems involving ratio. In KS4 these skills are recapped and the focus will be more on problem solving questions using your knowledge of ratio.
Download this 15 Ratio Questions And Practice Problems (KS3 & KS4) Worksheet
Help your students prepare for their Maths GSCE with this free Ratio worksheet of 15 multiple choice questions and answers.
Download Free Now!Proportion and ratio
Ratio often appears alongside proportion and the two topics are related. Whereas ratio compares the size of different parts of a whole, proportion compares the size of one part with the whole. Given a ratio, we can find a proportion and vice versa.
Take the example of a box containing 7 counters; 3 red counters and 4 blue counters:
The ratio of red counters:blue counters is 3:4.
For every 3 red counters there are four blue counters.
The proportion of red counters is \frac{3}{7} and the proportion of blue counters is \frac{4}{7}
3 out of every 7 counters are red and 4 out of every 7 counters are blue.
Direct proportion and inverse proportion
In KS4, we learn about direct proportion and inverse proportion. When two things are directly proportional to each other, one can be written as a multiple of the other and therefore they increase at a fixed ratio.
How to solve a ratio problem
When looking at a ratio problem, the key pieces of information that you need are what the ratio is, whether you have been given the whole amount or a part of the whole and what you are trying to work out.
If you have been given the whole amount you can follow these steps to answer the question:
- Add together the parts of the ratio to find the total number of shares
- Divide the total amount by the total number of shares
- Multiply by the number of shares required
If you have been been given a part of the whole you can follow these steps:
- Identify which part you have been given and how many shares it is worth
- Use equivalent ratios to find the other parts
- Use the values you have to answer your problem
Ratio tables are another technique for solving ratio problems.
How to solve a proportion problem
As we have seen, ratio and proportion are strongly linked. If we are asked to find what proportion something is of a total, we need to identify the amount in question and the total amount. We can then write this as a fraction:
Proportion problems can often be solved using scaling. To do this you can follow these steps:
- Identify the values that you have been given which are proportional to each other
- Use division to find an equivalent relationship
- Use multiplication to find the required relationship
Real life ratio problems and proportion problems
Ratio is all around us. Let’s look at some examples of where we may see ratio and proportion:
Cooking ratio question
When making yoghurt, the ratio of starter yogurt to milk should be 1:9. I want to make 1000ml of yoghurt. How much milk should I use?
Here we know the full amount – 1000ml.
The ratio is 1:9 and we want to find the amount of milk.
- Total number of shares
= 1 + 9 = 10 - Value of each share:
1000 ÷ 10 = 100 - The milk is
9 shares so9 × 100 = 900
I need to use 900ml of milk.
Maps ratio question
The scale on a map is 1:10000. What distance would 3.5cm on the map represent in real life?
Here we know one part is 3.5. We can use equivalent ratios to find the other part.
The distance in real life would be 35000cm or 350m.
Speed proportion question
I travelled 60 miles in 2 hours. Assuming my speed doesn’t change, how far will I travel in 3 hours?
This is a proportion question.
- I travelled 60 miles in 2 hours.
- Dividing by 2, I travelled 30 miles in one hour
- Multiplying by 3, I would travel 90 miles in 3 hours
KS2 ratio questions
Ratio is introduced in KS2. Writing and simplifying ratios is explored and the idea of dividing quantities in a given ratio is introduced using word problems such as the question below, before being linked with the mathematical notation of ratio.
Example KS2 worded question
Richard has a bag of 30 sweets. Richard shares the sweets with a friend. For every 3 sweets Richard eats, he gives his friend 2 sweets. How many sweets do they each eat?
KS3 ratio questions
In KS3 ratio questions ask you to write and simplify a ratio, to divide quantities into a given ratio and to solve problems using equivalent ratios.
You may also like:
Ratio questions year 7
1. In Lucy’s class there are 12 boys and 18 girls. Write the ratio of girls:boys in its simplest form.
The question asks for the ratio girls:boys so girls must be first and boys second. It also asks for the answer in its simplest form.
2. Gertie has two grandchildren, Jasmine, aged 2, and Holly, aged 4. Gertie divides £30 between them in the ratio of their ages. How much do they each get?
Jasmine £15, Holly £15
Jasmine £15, Holly £7.50
Jasmine £10, Holly £20
Jasmine £2, Holly £4
£30 is the whole amount.
Gertie divides £30 in the ratio 2:4.
The total number of shares is 2 + 4 = 6.
Each share is worth £30 ÷ 6 = £5.
Jasmine gets 2 shares, 2 x £5 = £10.
Holly gets 4 shares, 4 x £5 = £20.
Ratio questions year 8
3. The ratio of men:women working in a company is 3:5. What proportion of the employees are women?
In this company, the ratio of men:women is 3:5 so for every 3 men there are 5 women.
This means that for every 8 employees, 5 of them are women.
Therefore \frac{5}{8} of the employees are women.
4. The ratio of cups of flour:cups of water in a pizza dough recipe is 9:4. A pizza restaurant makes a large quantity of dough, using 36 cups of flour. How much water should they use?
16 Cups
13 Cups
11 Cups
81 Cups
The ratio of cups of flour:cups of water is 9:4. We have been given one part so we can work this out using equivalent ratios.
Ratio questions year 9
5. The angles in a triangle are in the ratio 3:4:5. Work out the size of each angle.
30^{\circ} , 40^{\circ} and 50^{\circ}
22.5^{\circ}, 30^{\circ} and 37.5^{\circ}
60^{\circ} , 60^{\circ} and 60^{\circ}
45^{\circ} , 60^{\circ} and 75^{\circ}
The angles in a triangle add up to 180 ^{\circ} . Therefore 180 ^{\circ} is the whole and we need to divide 180 ^{\circ} in the ratio 3:4:5.
The total number of shares is 3 + 4 + 5 = 12.
Each share is worth 180 ÷ 12 = 15 ^{\circ} .
3 shares is 3 x 15 = 45 ^{\circ} .
4 shares is 4 x 15 = 60 ^{\circ} .
5 shares is 5 x 15 = 75 ^{\circ} .
6. Paint Pro makes pink paint by mixing red paint and white paint in the ratio 3:4.
Colour Co makes pink paint by mixing red paint and white paint in the ratio 5:7.
Which company uses a higher proportion of red paint in their mixture?
They are the same
Paint Pro
Colour Co
It is impossible to tell
The proportion of red paint for Paint Pro is \frac{3}{7}
The proportion of red paint for Colour Co is \frac{5}{12}
We can compare fractions by putting them over a common denominator using equivalent fractions
\frac{3}{7} = \frac{36}{84} \hspace{3cm} \frac{5}{12}=\frac{35}{84}
\frac{3}{7} is a bigger fraction so Paint Pro uses a higher proportion of red paint.
KS4 ratio questions
In KS4 we apply the knowledge that we have of ratios to solve different problems. Ratio is an important topic in all exam boards, including Edexcel, AQA and OCR. Ratio questions can be linked with many different topics, for example similar shapes and probability, as well as appearing as problems in their own right.
Ratio GCSE exam questions foundation
7. The students in Ellie’s class walk, cycle or drive to school in the ratio 2:1:4. If 8 students walk, how many students are there in Ellie’s class altogether?
We have been given one part so we can work this out using equivalent ratios.
The total number of students is 8 + 4 + 16 = 28
8. A bag contains counters. 40% of the counters are red and the rest are yellow.
Write down the ratio of red counters:yellow counters. Give your answer in the form 1:n.
If 40% of the counters are red, 60% must be yellow and therefore the ratio of red counters:yellow counters is 40:60. Dividing both sides by 40 to get one on the left gives us
Since the question has asked for the ratio in the form 1:n, it is fine to have decimals in the ratio.
9. Rosie and Jim share some sweets in the ratio 5:7. If Jim gets 12 sweets more than Rosie, work out the number of sweets that Rosie gets.
Jim receives 2 shares more than Rosie, so 2 shares is equal to 12.
Therefore 1 share is equal to 6. Rosie receives 5 shares: 5 × 6 = 30.
10. Rahim is saving for a new bike which will cost £480. Rahim earns £1500 per month. Rahim spends his money on bills, food and extras in the ratio 8:3:4. Of the money he spends on extras, he spends 80% and puts 20% into his savings account.
How long will it take Rahim to save for his new bike?
1 month
6 months
3 months
5 months
Rahim’s earnings of £1500 are divided in the ratio of 8:3:4.
The total number of shares is 8 + 3 + 4 = 15.
Each share is worth £1500 ÷ 15 = £100.
Rahim spends 4 shares on extras so 4 × £100 = £400.
20% of £400 is £80.
The number of months it will take Rahim is £480 ÷ £80 = 6
Ratio GCSE exam questions higher
11. The ratio of milk chocolates:white chocolates in a box is 5:2. The ratio of milk chocolates:dark chocolates in the same box is 4:1.
If I choose one chocolate at random, what is the probability that that chocolate will be a milk chocolate?
To find the probability, we need to find the fraction of chocolates that are milk chocolates. We can look at this using equivalent ratios.
To make the ratios comparable, we need to make the number of shares of milk chocolate the same in both ratios. Since 20 is the LCM of 4 and 5 we will make them both into 20 parts.
We can now say that milk:white:dark is 20:8:5. The proportion of milk chocolates is \frac{20}{33} so the probability of choosing a milk chocolate is \frac{20}{33} .
12. In a school the ratio of girls:boys is 2:3.
25% of the girls have school dinners.
30% of the boys have school dinners.
What is the total percentage of students at the school who have school dinners?
In this question you are not given the number of students so it is best to think about it using percentages, starting with 100%.
100% in the ratio 2:3 is 40%:60% so 40% of the students are girls and 60% are boys.
25% of 40% is 10%.
30% of 60% is 18%.
The total percentage of students who have school dinners is 10 + 18 = 28%.
13. For the cuboid below, a:b = 3:1 and a:c = 1:2.
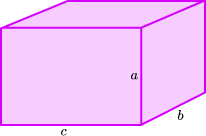
Find an expression for the volume of the cuboid in terms of a.
If a:b = 3:1 then b=\frac{1}{3}a
If a:c = 1:2 then c=2a.
Difficult ratio GCSE questions
14. Bill and Ben win some money in their local lottery. They share the money in the ratio 3:4. Ben decides to give £40 to his sister. The amount that Bill and Ben have is now in the ratio 6:7.
Calculate the total amount of money won by Bill and Ben.
£560
£70
£140
£600
Initially the ratio was 3:4 so Bill got £3a and Ben got £4a. Ben then gave away £40 so he had £(4a-40).
The new ratio is 3a:4a-40 and this is equal to the ratio 6:7.
Since 3a:4a-40 is equivalent to 6:7, 7 lots of 3a must be equal to 6 lots of 4a-40.
\begin{aligned} \\ 7 \times 3a &= 6 \times (4a-40)\\\\ 21a&=24a-240\\\\ 3a&=240\\\\ a&=80 \end{aligned}
The initial amounts were 3a:4a. a is 80 so Bill received £240 and Ben received £320.
The total amount won was £560.
15. On a farm the ratio of pigs:goats is 4:1. The ratio of pigs:piglets is 1:6 and the ratio of gots:kids is 1:2.
What fraction of the animals on the farm are babies?
The easiest way to solve this is to think about fractions.
\\ \frac{4}{5} of the animals are pigs, \frac{1}{5} of the animals are goats.
\frac{1}{7} of the pigs are adult pigs, so \frac{1}{7} of \frac{4}{5} is \frac{1}{7} \times \frac{4}{5} = \frac{4}{35}
\frac{6}{7} of the pigs are piglets, so \frac{6}{7} of \frac{4}{5} is \frac{6}{7} \times \frac{4}{5} = \frac{24}{35}
\frac{1}{3} of the goats are adult goats, so \frac{1}{3} of \frac{1}{5} is \frac{1}{3} \times \frac{1}{5} = \frac{1}{15}
\frac{2}{3} of the goats are kids, so \frac{2}{3} of \frac{1}{5} is \frac{2}{3} \times \frac{1}{5} = \frac{2}{15}
The total fraction of baby animals is \frac{24}{35} + \frac{2}{15} = \frac{72}{105} +\frac{14}{105} = \frac{86}{105}
Looking for more ratio questions and resources?
Third Space Learning’s free GCSE maths resource library contains detailed lessons with step-by-step instructions on how to solve ratio problems, as well as worksheets with ratio and proportion practice questions and more GCSE exam questions.
Take a look at the Ratio lessons today – more are added every week.
If you’re also looking for other topics, try our GCSE maths questions blog!
Looking for more KS3 and KS4 maths questions?
Try these:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn how tutors develop pupils’ maths fluency or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
