15 Trigonometry Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included
Trigonometry questions address the relationship between the angles of a triangle and the lengths of its sides. By using our knowledge of the rules of trigonometry we can calculate missing angles or sides when we have been given some of the information.
Here we’ve provided 15 trigonometry questions to provide students with practice at the various sorts of trigonometry problems and GCSE exam style questions you can expect in KS3 and KS4 trigonometry.
Trigonometry in the real world
Trigonometry is used by architects, engineers, astronomers, crime scene investigators, flight engineers and many others.
Trigonometry in KS3 and KS4
In KS3 we learn about the trigonometric ratios sin, cos and tan and how we can use these to calculate sides and angles in right angled triangles. In KS4 trigonometry involves applying this to a variety of situations as well as learning the exact values of sin, cos and tan for certain angles.
In the higher GCSE syllabus we learn about the sine rule, the cosine rule, a new formula for the area of a triangle and we apply trigonometry to 3D shapes. In A Level maths trigonometry is developed further but that is not the focus of the trigonometry questions here.
GCSE MATHS 2025: STAY UP TO DATE
Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2025. We’re analysing each paper during the course of the 2025 GCSEs in order to identify the key topic areas to focus on for your revision.
GCSE dates 2025
GCSE results 2025 (when published)
GCSE results 2024
Analysis of GCSE Maths Paper 1 (2024)
Analysis of GCSE Maths Paper 2 (2024)
Analysis of GCSE Maths Paper 3 (2024)
Summary of ALL GCSE Maths Papers (2024)
How to answer trigonometry questions
The way to answer trigonometry questions depends on whether it is a right angled triangle or not.
Download this 15 Trigonometry Questions And Practice Problems (KS3 & KS4) Worksheet
Help your students prepare for their Maths GSCE with this free Trigonometry worksheet of 15 multiple choice questions and answers.
Download Free Now!How to answer trigonometry questions: right-angled triangles
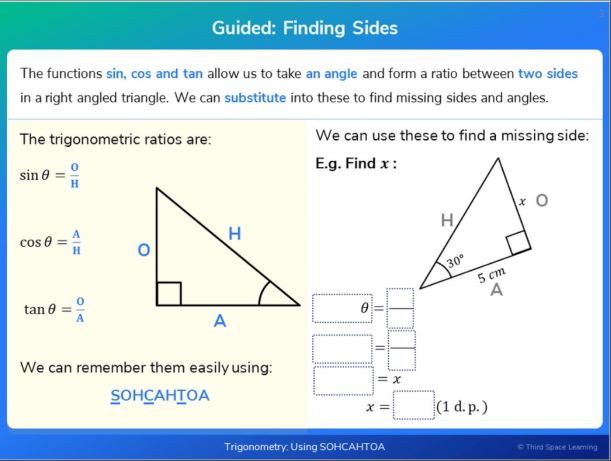
If your trigonometry question involves a right angled triangle, you can apply the following relationships ie SOH, CAH, TOA
To answer the trigonometry question:
1. Establish that it is a right angled triangle.
2. Label the opposite side (opposite the angle) the adjacent side (next to the angle) and the hypotenuse (longest side opposite the right angle).
3. Use the following triangles to help us decide which calculation to do:
How to answer trigonometry questions – non-right angled triangles
If the triangle is not a right angled triangle then we need to use the sine rule or the cosine rule.
There is also a formula we can use for the area of a triangle, which does not require us to know the base and height of the triangle.
To answer the trigonometry question:
- Establish that it is not a right angled triangle.
- Label the sides of the triangle using lower case a, b, c.
- Label the angles of the triangle using upper case A, B and C.
- Opposite sides and angles should use the same letter so for example angle C is opposite to side c.
KS3 trigonometry questions
In KS3 trigonometry questions focus on understanding of sin, cos and tan (SOHCAHTOA) to calculate missing sides and angles in right triangles.
You may also like:
KS3 trigonometry questions – missing side
1. A zip wire runs between two posts, 25m apart. The zip wire is at an angle of 10^{\circ} to the horizontal. Calculate the length of the zip wire.
\begin{aligned} H&=\frac{A}{\cos(\theta)}\\\\ H&=\frac{25}{\cos(10)}\\\\ H&=25.4\mathrm{m} \end{aligned}
2. A surveyor wants to know the height of a skyscraper. He places his inclinometer on a tripod 1m from the ground. At a distance of 50m from the skyscraper, he records an angle of elevation of 82^{\circ} .
What is the height of the skyscraper? Give your answer to one decimal place.
\begin{aligned} O&=\tan(\theta) \times A\\\\ O&=\tan(82) \times 50\\\\ O&=355.8\mathrm{m} \end{aligned}
Total height = 355.8+1=356.8m.
3. Triangle ABC is isosceles. Work out the height of triangle ABC.
To solve this we split the triangle into two right angled triangles.
\begin{aligned} O&=\tan(\theta) \times A\\\\ O&=\tan(71) \times 6\\\\ O&=17.4\mathrm{cm} \end{aligned}
KS3 trigonometry questions – missing angles
4. A builder is constructing a roof. The wood he is using for the sloped section of the roof is 4m long and the peak of the roof needs to be 2m high. What angle should the piece of wood make with the base of the roof?
\begin{aligned} \sin(\theta)&=\frac{O}{H}\\\\ \sin(\theta)&=\frac{2}{4}\\\\ \theta&=sin^{-1}(\frac{2}{4})\\\\ \theta&=30^{\circ} \end{aligned}
5. A ladder is leaning against a wall. The ladder is 1.8m long and the bottom of the ladder is 0.5m from the base of the wall. To be considered safe, a ladder must form an angle of between 70^{\circ} and 80^{\circ} with the floor. Is this ladder safe?
Yes
No
Not enough information
\begin{aligned} \cos(\theta)&=\frac{A}{H}\\\\ \cos(\theta)&=\frac{0.5}{1.8}\\\\ \theta&=cos^{-1}(\frac{0.5}{1.8})\\\\ \theta&=73.9^{\circ} \end{aligned}
Yes it is safe.
6. A helicopter flies 40km east followed by 105km south. On what bearing must the helicopter fly to return home directly?
\begin{aligned} \tan(\theta)&=\frac{O}{A}\\\\ \tan(\theta)&=\frac{40}{105}\\\\ \theta&=tan^{-1}(\frac{40}{105})\\\\ \theta&=21^{\circ} \end{aligned}
Since bearings are measured clockwise from North, we need to do 360-21=339^{\circ}.
KS4 trigonometry questions
In KS4 maths, trigonometry questions ask students to solve a variety of problems including multi step problems and real life problems. We also need to be familiar with the exact values of the trigonometric functions at certain angles.
In the higher syllabus we look at applying trigonometry to 3D problems as well as using the sine rule, cosine rule and area of a triangle.
Trigonometry is covered by all exam boards, including Edexcel, AQA and OCR.
KS4 trigonometry questions – SOHCAHTOA
7. Calculate the size of angle ABC. Give your answer to 3 significant figures.
\begin{aligned} A&=\frac{O}{\tan(\theta)}\\\\ A&=\frac{10}{\tan(28)}\\\\ A&=18.81\mathrm{m} \end{aligned}
\begin{aligned} \cos(\theta)&=\frac{A}{H}\\\\ \cos(\theta)&=\frac{18.81}{24}\\\\ \theta&=cos^{-1}(\frac{18.81}{24})\\\\ \theta&=38.4^{\circ} \end{aligned}
8. Kevin’s garden is in the shape of an isosceles trapezium (the sloping sides are equal in length). Kevin wants to buy enough grass seed for his garden. Each box of grass seed covers 15m^2 . How many boxes of grass seed will Kevin need to buy?
To calculate the area of the trapezium, we first need to find the height. Since it is an isosceles trapezium, it is symmetrical and we can create a right angled triangle with a base of \frac{10-5}{2} .
\begin{aligned} O&=\tan(\theta)\times A\\\\ O&=\tan(78)\times2.5\\\\ O&=11.76\mathrm{m} \end{aligned}
We can then find the area of the trapezium:
\begin{aligned} \text{Area }&=\frac{1}{2}(a+b)h\\\\ \text{Area }&=\frac{1}{2}(5+10)\times 11.76\\\\ \text{Area }&=88.2\mathrm{m}^{2} \end{aligned}
Number of boxes: 88.215=5.88
Kevin will need 6 boxes.
KS4 trigonometry questions – exact values
9. Which of these values cannot be the value of \sin(\theta) ?
10. . Write 4sin(60) + 3tan(60) in the form a\sqrt{k}.
\begin{aligned} 4\sin(60)+3\tan(60) &= 4\times \frac{\sqrt{3}}{2}+3\sqrt{3}\\\\ &=2\sqrt{3}+3\sqrt{3}\\\\ &=5\sqrt{3} \end{aligned}
KS4 trigonometry questions – 3D trigonometry
11.
Work out angle a, between the line AG and the plane ADHE.
We need to begin by finding the length AH by looking at the triangle AEH and using pythagoras theorem.
\begin{aligned} &AH^2=14^2+3^2 \\\\ &AH^2=205 \\\\ &AH=14.32cm \end{aligned}
We can then find angle a by looking at the triangle AGH.
\begin{aligned} \tan(\theta)&=\frac{O}{A}\\\\ \tan(\theta)&=\frac{4}{14.32}\\\\ \theta&=tan^{-1}(\frac{4}{14.32})\\\\ \theta&=15.6^{\circ} \end{aligned}
12. Work out the length of BC.
First we need to find the length DC by looking at triangle CDE.
\begin{aligned} H&=\frac{O}{\sin(\theta)}\\\\ H&=\frac{15}{\sin(52)}\\\\ H&=19.04\mathrm{cm} \end{aligned}
We can then look at triangle BAC.
\begin{aligned} H&=\frac{o}{\sin(\theta)}\\\\ H&=\frac{19.04}{\sin(40)}\\\\ H&=29.6\mathrm{mm} \end{aligned}
KS4 trigonometry questions – sine/cosine rule
13. Ship A sails 40km due West and ship B sails 65km on a bearing of 050^{\circ} . Find the distance between the two ships.
The angle between their two paths is 90+50=140^{\circ} .
\begin{aligned}
a^{2}&=b^{2}+c^{2}-2bc \cos(A)\\\\
a^{2}&=40^{2}+65^{2}-2\times 40 \times 65 \cos(140)\\\\
a^{2}&=5825-5200 \cos(140)\\\\
a^{2}&=9808.43\\\\
a&=99.0\mathrm{km}
\end{aligned}
14. Find the size of angle B.
First we need to look at the right angled triangle.
\begin{aligned} &O=tan()A\\\\ &O=tan(22)23\\\\ &O=9.29cm \end{aligned}
Then we can look at the scalene triangle.
\begin{aligned} \frac{\sin(A)}{A}&=\frac{\sin(B)}{B}\\\\ \frac{\sin(51)}{15}&=\frac{\sin(B)}{9.29}\\\\ 9.29\times \frac{\sin(51)}{15} &= \sin(B)\\\\ 0.481&=\sin(B)\\\\ \sin^{-1}(0.481)&=B\\\\ 28.8^{\circ}&=B \end{aligned}
KS4 trigonometry questions – area of a triangle
Free GCSE maths revision resources for schools
As part of the Third Space Learning offer to schools, the personalised online GCSE maths tuition can be supplemented by hundreds of free GCSE maths revision resources from the secondary maths resources library including:
– GCSE maths past papers
– GCSE maths predicted papers
– GCSE maths worksheets
– GCSE maths questions
– GCSE maths topic list
Looking for more KS3 and KS4 maths questions?
Try these:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist GCSE maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 169,000 primary and secondary students become more confident, able mathematicians.
Learn about the GCSE revision programme or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
