15 Pythagoras Theorem Questions And Practice Problems (KS3 & KS4)
Pythagoras Theorem questions involve using the relationship between the sides of a right angled triangle to work out missing side lengths in triangles. Pythagoras Theorem is usually introduced towards the end of KS3 and is used to solve a variety of problems across KS4.
Here, you’ll find a selection of Pythagoras Theorem questions that demonstrate the different types of questions you are likely to encounter in KS3 and KS4, including several GCSE exam-style questions.
GCSE MATHS 2025: STAY UP TO DATE
Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2025. We’re analysing each paper during the course of the 2025 GCSEs in order to identify the key topic areas to focus on for your revision.
GCSE dates 2025
GCSE results 2025 (when published)
GCSE results 2024
Analysis of GCSE Maths Paper 1 (2024)
Analysis of GCSE Maths Paper 2 (2024)
Analysis of GCSE Maths Paper 3 (2024)
Summary of ALL GCSE Maths Papers (2024)
What is Pythagoras Theorem?
Pythagoras Theorem is the geometric theorem that states that the square of the hypotenuse (longest side) of a right angled triangle is equal to the sum of the squares of the two shorter sides of the triangle.
This can be written as a^2+b^2=c^2 for a triangle labelled like this:
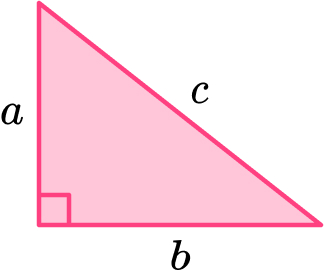
How to answer Pythagoras Theorem questions
- Label the sides of the triangle a, b and c.
Note that the hypotenuse, the longest side of a right angled triangle, is opposite the right angle and will always be labelled \textbf{c}. The other two sides can be labelled a and b either way around.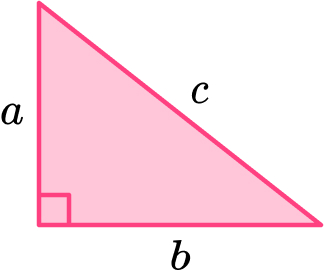
- Write down the formula and substitute the values.
a^2+b^2=c^2 - Work out the answer.
You may be asked to give your answer in an exact form or round to a given degree of accuracy, such as a certain number of decimal places or significant figures.
Pythagoras Theorem in real life
Pythagoras Theorem has many real life uses, including in architecture and construction, navigation and surveying.
Pythagoras Theorem in KS3
Pythagoras Theorem is usually introduced towards the end of KS3.
The emphasis in KS3 is on students being able to:
- Correctly label a right angled triangle;
- Substitute values into the formula in order to work out the hypotenuse or one of the shorter sides.
15 Pythagoras Theorem Questions And Practice Problems Worksheet
Help your students prepare for their Maths GCSE with this free Pythagoras Theorem worksheet of 15 questions, includes answers and mark scheme
Download Free Now!
Pythagoras Theorem KS3 questions
Non-calculator questions
1. A ship sails 6 \, km East and then 8 \, km North. Find the ship’s distance from its starting point.
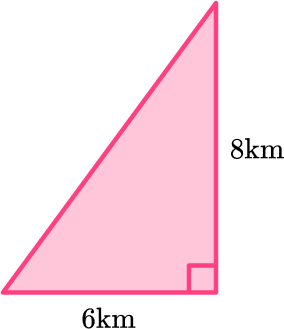
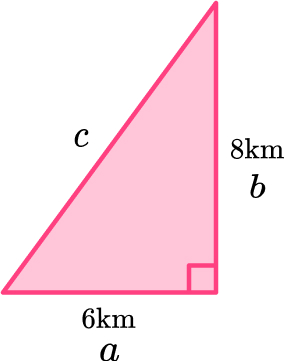
\begin{aligned} a^2+b^2&=c^2\\ 6^2+8^2&=c^2\\ 36+64&=c^2\\ 100&=c^2\\ c&=\sqrt{100}\\ c&=10 \, km \end{aligned}
The ship is 10 kilometres from its starting point.
2. A ladder is 5 \, m long. The base of the ladder is 3 \, m from the base of a vertical wall. How far up the wall does the ladder reach?
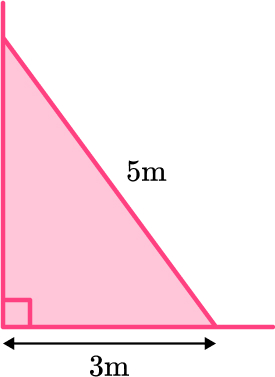
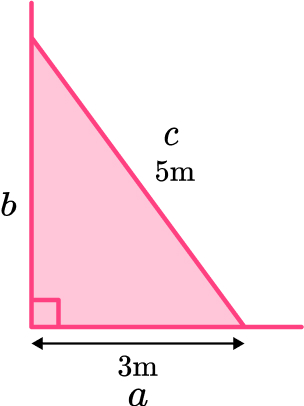
\begin{aligned} b^{2}&=c^{2}-a^{2}\\ b^{2}&=5^{2}-3^{2}\\ b^{2}&=25-9\\ b^{2}&=16\\ b&=\sqrt{16}\\ b&=4 \, m \end{aligned}
The ladder reaches 4 meters up the wall.
Calculator questions
For these questions, round your answers to 3 significant figures.
3. Alex and Sam start from the same point. Alex walks 400 metres west. Sam walks x metres south, until they are 600 \, m apart from each other. How far does Sam walk?
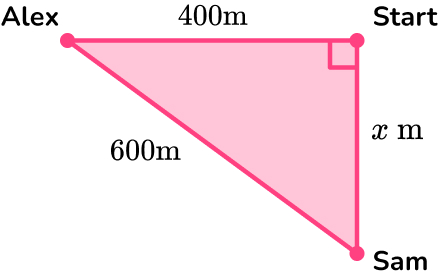
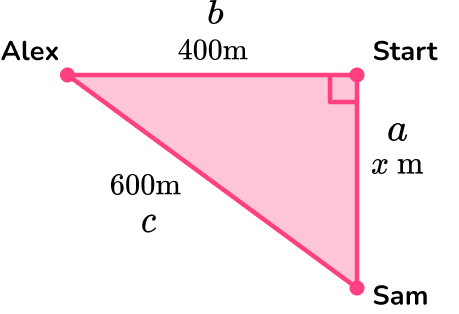
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ x^{2}&=600^{2}-400^{2}\\ x^{2}&=360000-160000\\ x^{2}&=200000\\ x&=\sqrt{200000}\\ x&=447.2135955\\ x&=447 \, m ~\text{(3sf)} \end{aligned}
4. A television’s size is the measurement from the upper left hand corner of the television to the bottom right hand corner. Find the size of this television.
75 inches
150 inches
39.7 inches
55.1 inches
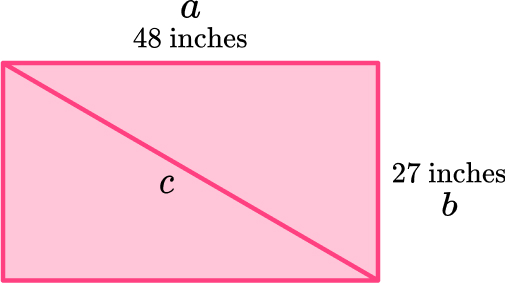
\begin{aligned} a^2+b^2&=c^2\\ 48^2+27^2&=c^2\\ 2304+729&=c^2\\ 3033&=c^2\\ c&=\sqrt{3033}\\ c&=55.07267925\\ c&=55.1 \, \mathrm{inches} ~ \text{(3sf)} \end{aligned}
Pythagoras Theorem in KS4
In KS4, students use Pythagoras Theorem to solve a variety of problems. Examples include:
- real life word problems
- coordinate problems
- multi-step problems
- 3D problems
Pythagoras Theorem may feature in questions alongside other topics, such as trigonometry, circle theorems or algebra.
The process for solving any Pythagoras Theorem problem always begins by identifying the relevant right angled triangle and labelling the sides a, b and c. If there is not a diagram in the question, it can be helpful to draw one.
Foundation GCSE Questions
Where necessary, round your answers to 3 significant figures.
5. The pole of a sailing boat is supported by a rope from the top of the pole to an anchor point on the deck. The pole is 4 \, m long and the rope is 4.5 \, m long. Calculate the distance from the base of the pole to the anchor point of the rope on the deck.
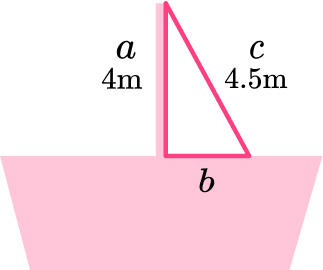
\begin{aligned} b^{2}&=c^{2}-a^{2}\\ b^{2}&=4.5^{2}-4^{2}\\ b^{2}&=20.25-16\\ b^{2}&=4.25\\ b&=\sqrt{4.25}\\ b&=2.061552813\\ b&=2.06 \, m ~\text{(3sf)} \end{aligned}
6. Work out the length of the diagonal of a square with 8 \, cm sides.
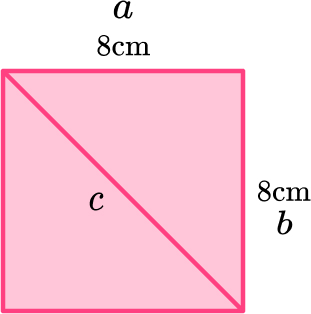
\begin{aligned} a^2+b^2&=c^2\\ 8^2+8^2&=c^2\\ 64+64&=c^2\\ 128&=c^2\\ c&=\sqrt{128}\\ c&=11.3137085\\ c&=11.3 \, cm ~ \text{(3sf)} \end{aligned}
The diagonal of the square has a length of 11.3 centimetres.
7. ABC is an isosceles triangle.
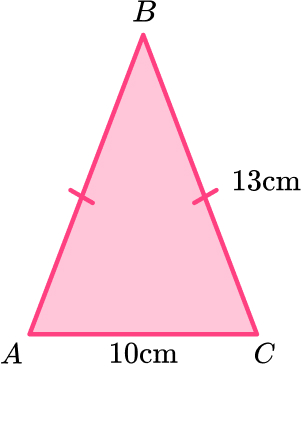
Work out the height of the triangle.
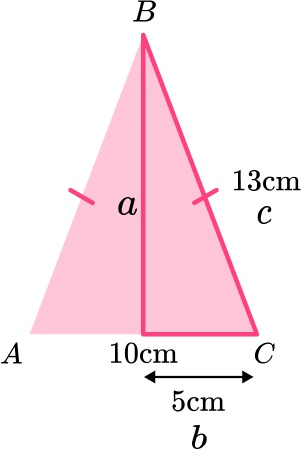
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ a^{2}&=13^{2}-5^{2}\\ a^{2}&=169-25\\ a^{2}&=144\\ a&=\sqrt{144}\\ a&=12 \, cm \end{aligned}
8. ABCD is an isosceles trapezium.
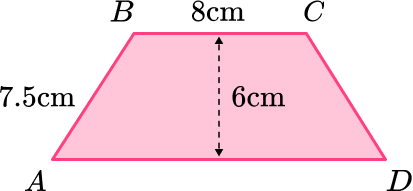
Work out the length of AD.
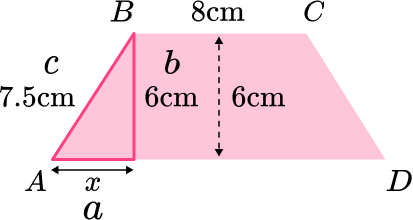
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ x^{2}&=7.5^{2}-6^{2}\\ x^{2}&=56.25-36\\ x^{2}&=20.25\\ x&=\sqrt{20.25}\\ x&=4.5 \, cm \end{aligned}
AD=4.5+8+4.5=17 \, cm
9. Here is a cm square grid. Calculate the distance between the points A and B.
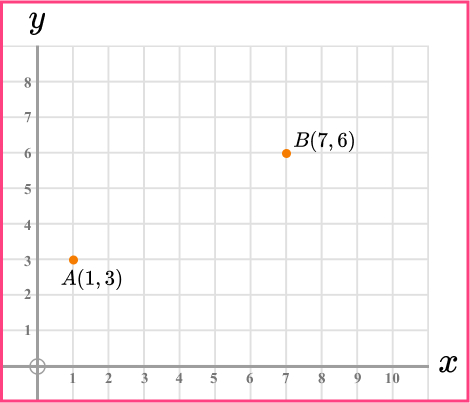
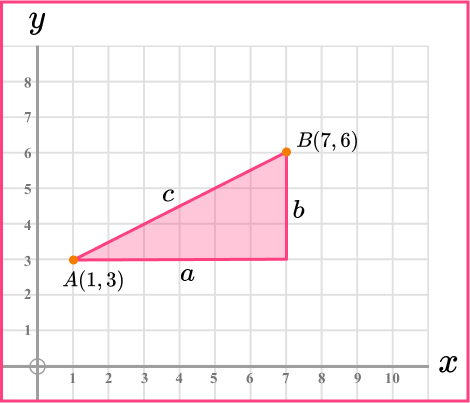
\begin{aligned} a^2+b^2&=c^2\\ 6^2+3^2&=c^2\\ 36+9&=c^2\\ 45&=c^2\\ c&=\sqrt{45}\\ c&=6.708203932\\ c&=6.7 \, cm ~ \text{(3sf)} \end{aligned}
10. Which is a right angled triangle?
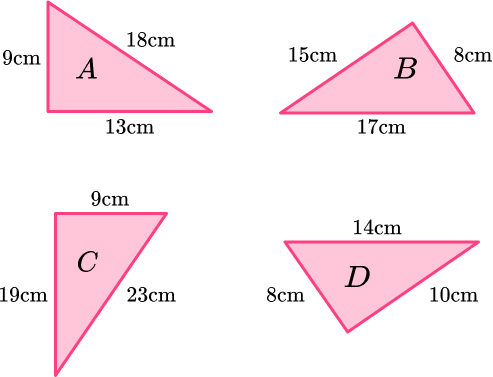
Not a right angled triangle because Pythagoras Theorem doesn’t work.
\begin{aligned} \text{B: } 8^{2}+15^{2}&=289\\ 17^{2}&=289 \\ \end{aligned}
Right angled triangle because Pythagoras Theorem works.
\begin{aligned} \text{C: } 9^{2}+19^{2}&=442\\ 23^{2}&=529 \\ \end{aligned}
Not a right angled triangle because Pythagoras Theorem doesn’t work.
\begin{aligned} \text{D: } 8^{2}+10^{2}&=164\\ 14^{2}&=196 \\ \end{aligned}
Not a right angled triangle because Pythagoras Theorem doesn’t work.
11. PQRS is made from two right angled triangles.
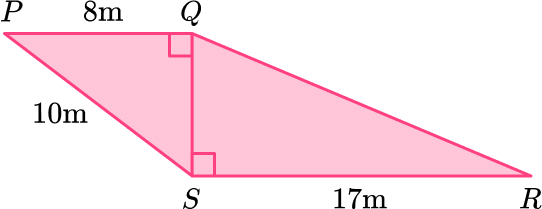
Work out the length of QR.
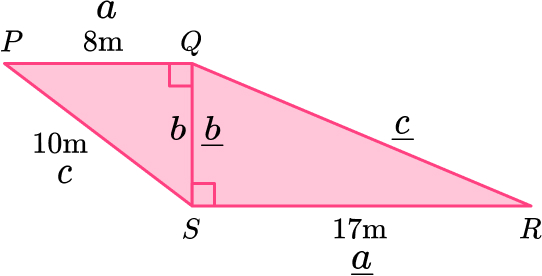
Triangle \text{PQS:}
\begin{aligned} \\ b^{2}&=c^{2}-a^{2}\\ b^{2}&=10^{2}-8^{2}\\ b^{2}&=100-64\\ b^{2}&=36\\ b&=\sqrt{36}\\ b&=6 \, m \end{aligned}
Triangle \text{QRS}
\begin{aligned} \\ a^2+b^2&=c^2\\ 17^2+6^2&=c^2\\ 289+36&=c^2\\ 325&=c^2\\ c&=\sqrt{325}\\ c&=18.02775638\\ c&=18.0 \, m ~ \text{(3sf)} \end{aligned}12. Here is a pattern made from right angled triangles. Work out the length x.
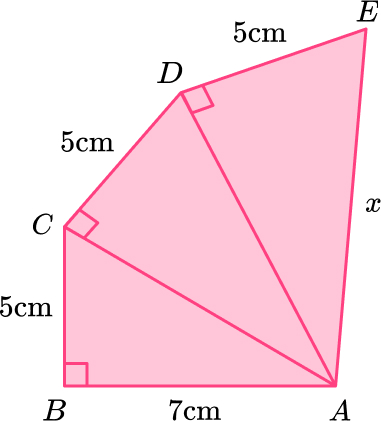
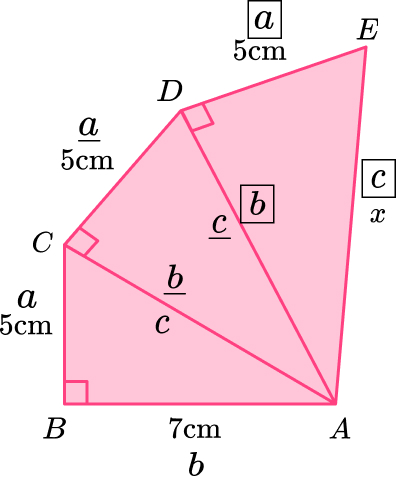
Triangle \text{ABC:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 5^2+7^2&=c^2\\ 74&=c^2\\ c&=\sqrt{74}\\ c&=8.602325267 \end{aligned}
Triangle \text{ACD:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 5^2+8.60232567^2&=c^2\\ 99&=c^2\\ c&=\sqrt{99}\\ c&=9.949874371 \end{aligned}
Triangle \text{ADE:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 5^2+9.949874371^2&=c^2\\ 124&=c^2\\ c&=\sqrt{124}\\ c&=11.13552873\\ c&=11.1 \, cm ~ \text{(3sf)} \end{aligned}Higher GCSE Questions
13. Here is a pyramid.
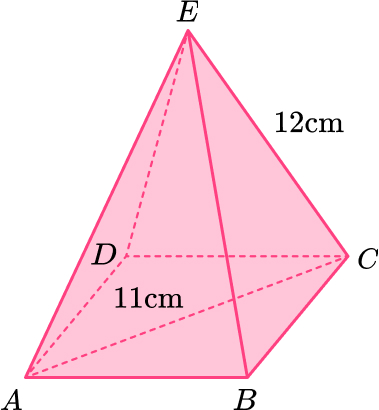
Work out the height of the pyramid.
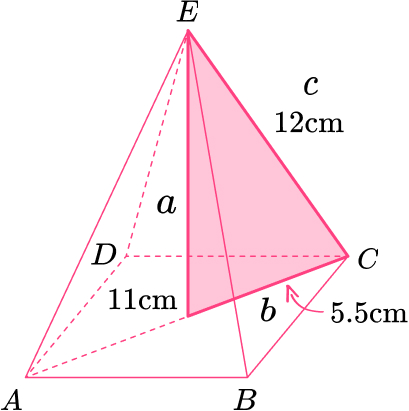
\begin{aligned} a^{2}&=c^{2}-b^{2}\\ a^{2}&=12^{2}-5.5^{2}\\ a^{2}&=113.75\\ a&=\sqrt{113.75}\\ a&=10.6653645 \mathrm{cm} \\ a&=10.7 \, cm ~ \text{(3sf)} \end{aligned}
14. Here is a cuboid.
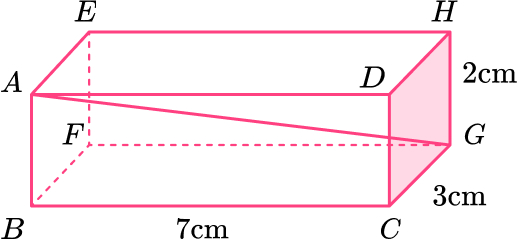
Work out the length AG.
Give your answer in its exact form.
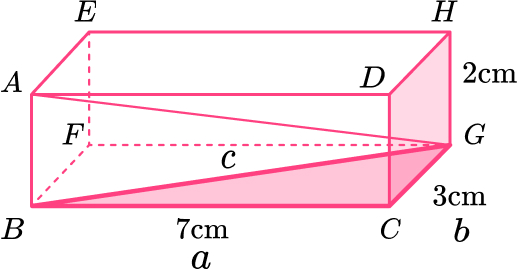
Length of \text{BG:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 7^2+3^2&=c^2\\ 58&=c^2\\ c&=\sqrt{58}\\ c&=7.615773106 \end{aligned}
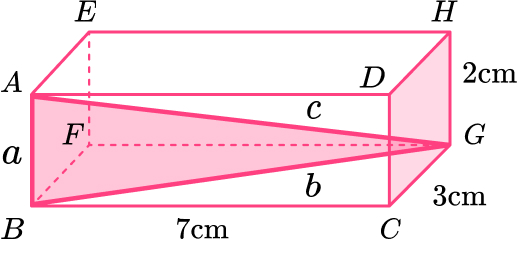
Length of \text{AG:}
\begin{aligned} \\ a^2+b^2&=c^2\\ 2^2+7.615773106^2&=c^2\\ 62&=c^2\\ c&=\sqrt{62} \, cm \end{aligned}15. Here is a right angled triangle.
Form an equation and use it to work out the value of x.
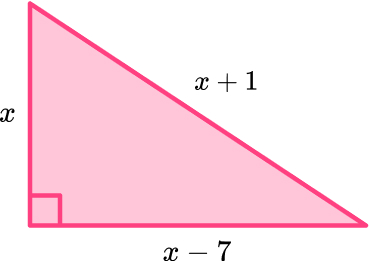
x=4 \, or \, x=12
x cannot be 4 as you cannot have a negative side length so x=12
Pythagoras Theorem is used to work out a missing length in a right angled triangle. If you have a right angled triangle and you know two of the lengths, label the sides of the triangle a, b and c ( c must be the hypotenuse – the longest side).
Pythagoras Theorem is a^2+b^2=c^2.
Substitute the values you know into Pythagoras Theorem and solve to find the missing side.
For a more detailed explanation, including a video and worked examples, see: Pythagoras Theorem.
The hypotenuse of a right angled triangle is the longest side. If you know the lengths of the other two sides, you can find the length of the hypotenuse by squaring the two shorter sides, adding those values together and then taking the square root.
By doing this you are finding c in a^2+b^2=c^2
If your triangle is a right angled triangle and you know two of the sides, you can use Pythagoras Theorem to find the length of the third side. To do this, label the sides a, b and c (with c being the hypotenuse – the longest side). Substitute the values you know into a^2+b^2=c^2 and solve to find the missing side.
Looking for more Pythagoras Theorem questions and resources?
Third Space Learning’s free GCSE maths resource library contains detailed lessons with step-by-step instructions on how to solve Pythagoras Theorem problems, as well as maths worksheets with practice questions and more GCSE exam questions, based on past Edexcel, OCR and AQA exam questions.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Â
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Â
Since 2013 these personalised one to one lessons have helped over 169,000 primary and secondary students become more confident, able mathematicians.
Â
Learn how tutors develop pupils’ maths fluency or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
