Pythagoras theorem

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Substitution Squares and square roots Solving equations Rounding numbers

This topic is relevant for:

GCSE Maths Geometry and Measure

Pythagoras Theorem

Here we will learn about Pythagoras theorem, including how to find sides of a right-angled triangle and how to use Pythagoras theorem to check if a triangle has a right angle or not.

There are also Pythagoras theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is Pythagoras theorem?

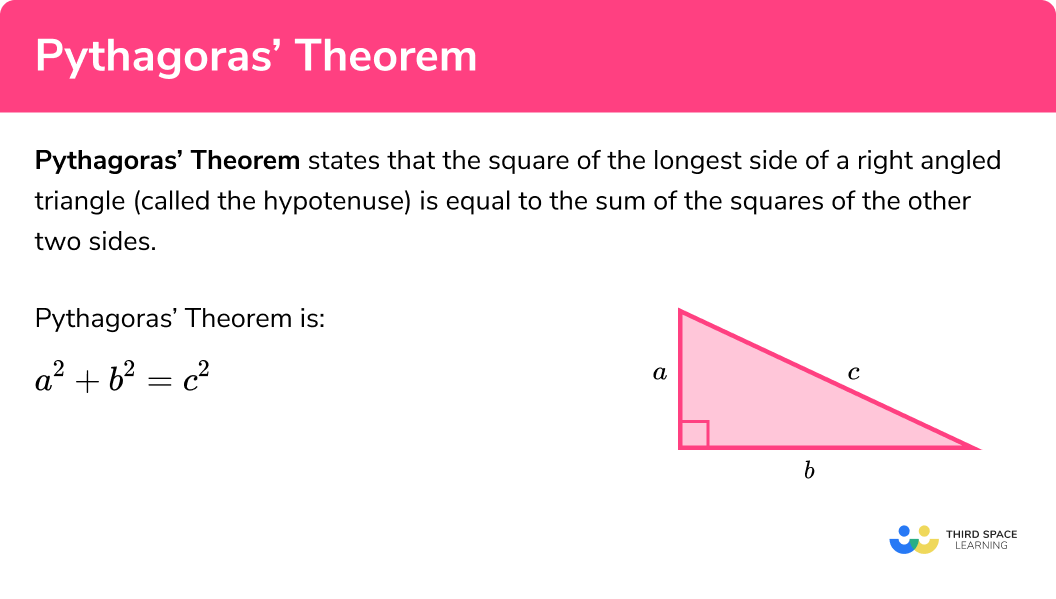
Pythagoras theorem states that the square of the longest side of a right angled triangle (called the hypotenuse) is equal to the sum of the squares of the other two sides.

Pythagoras theorem is:

\[a^2+b^2=c^2\]

Side $c$ is known as the hypotenuse, which is the longest side of a right-angled triangle and is opposite the right angle.
Side $a$ and side $b$ are known as the adjacent sides because they are adjacent (next to) the right angle.

If we know any two sides of a right angled triangle, we can use Pythagoras theorem to work out the length of the third side.

We can only use Pythagoras theorem with right-angled triangles.

E.g.
Let’s look at this right-angled triangle:

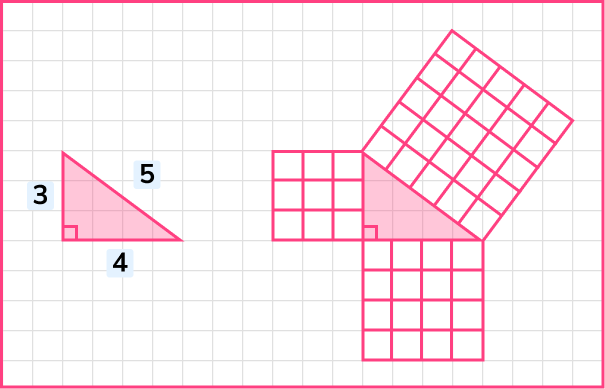
We can see that three squares have been drawn next to each of the sides of the triangle.
The area of the square with side length $3 = 3 \times 3=3^2=9$
The area of the square with side length $4 = 4\times 4=4^2=16$
The area of the square with side length $5 = 5\times5=5^2=25$

We can see that when we add together the areas of the squares on the two shorter sides we get the area of the square on the longest side.

\[9+16=25\]

We can see that when we square the lengths of the two shorter sides of a right angled triangle and add them together, we get the square of the longest side.

\[3^2+4^2=5^2\]

$3, 4, 5$ is known as a Pythagorean triple.
There are other Pythagorean triples such as $5, 12, 13$ and $8, 15, 17$ .

See also: 3D Pythagoras

What is Pythagoras theorem?

How to use Pythagoras theorem

In order to use Pythagoras theorem:

Label the sides of the triangle.
Write down the formula and apply the numbers.
Work out the answer.

Explain how to use Pythagoras theorem

Pythagoras theorem worksheet

Get your free pythagoras theorem worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Pythagoras theorem worksheet

Get your free pythagoras theorem worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Pythagoras theorem examples

Example 1: finding the length of the hypotenuse (finding the length of the longest side)

Find $x$ and give your answer to $2$ decimal places.

Label the sides of the triangle.

It is very important to label the hypotenuse (the longest side) correctly with $c$ . The adjacent sides, next to the right angle can be labelled $a$ and $b$ either way around as they are interchangeable.

2Write down the formula and apply the numbers.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ 3^2 + 8^2 &= x^2\\\\ x^2 &= 3^2+8^2\\\\ x^2 &= 9 + 64\\\\ x^2 &=73\\\\ x &= \sqrt{73} \end{aligned} \]

3Work out the answer.

Make sure you give your final answer in the correct form including units where appropriate.

\[x=\sqrt{73}=8.5440037…\]

The final answer is:

$x = 8.54$ cm to $2$ decimal places

An alternative method is to rearrange the formula and put the entire calculation into a calculator.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ c^2 &=a^2 + b^2 \\\\ c &= \sqrt{a^2 + b^2} \\\\ x &= \sqrt{3^2 + 8^2}\\\\ x &= 8.5440037… \end{aligned} \]

Example 2: finding the length of the hypotenuse (finding the length of the longest side)

Find $x$ and give your answer to $3$ significant figures:

Label the sides of the triangle.

Write down the formula and apply the numbers.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ 7^2 + 9^2 &= x^2\\\\ x^2 &= 7^2 + 9^2\\\\ x^2 &= 49+81\\\\ x^2 &= 130\\\\ x &=\sqrt{130} \end{aligned}\]

Work out the answer.

Make sure you give your final answer in the correct form including units where appropriate.

\[x=\sqrt{130}=11.40175.…\]

The final answer is:

$x = 11.4$ cm to $3$ significant figures

An alternative method is to rearrange the formula and put one calculation into a calculator.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ c^2 &=a^2 + b^2 \\\\ c &= \sqrt{a^2 + b^2} \\\\ x &= \sqrt{7^2 + 9^2}\\\\ x &= 11.40175… \end{aligned} \]

Example 3: finding an adjacent side (a short side)

Find $x$ and give your answer to $2$ significant figures:

Label the sides of the triangle.

We will label the short side we are trying to find as side $a$ .

Write down the formula and apply the numbers.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ x^2 + 5^2 &= 8^2\\\\ x^2+25 &= 64 \\\\ x^2 &= 64 – 25 \\\\ x^2 &= 39\\\\ x &=\sqrt{39} \end{aligned}\]

Work out the answer.

Make sure you give your final answer in the correct form; including units where appropriate.

\[x=\sqrt{39}=6.244997.…\]

The final answer is:

$x = 6.24$ cm to $2$ significant figures

An alternative method is to rearrange the formula and put one calculation into a calculator.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ a^2 &=c^2 – b^2 \\\\ a &= \sqrt{c^2 – b^2} \\\\ x &= \sqrt{8^2 – 5^2}\\\\ x &= 6.244997… \end{aligned} \]

Example 4: finding an adjacent side (a short side)

Find $x$ and give your answer to $3$ significant figures:

Label the sides of the triangle.

We will label the short side we are trying to find as side $a$ .

Write down the formula and apply the numbers.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ x^2 + 11^2 &= 20^2\\\\ x^2+121 &= 400 \\\\ x^2 &= 400 – 121 \\\\ x^2 &= 279\\\\ x &=\sqrt{279} \end{aligned}\]

Work out the answer.

Make sure you give your final answer in the correct form; including units where appropriate.

\[x=\sqrt{279}=16.70329.…\]

The final answer is:

$x = 16.7$ cm to $3$ significant figures

An alternative method is to rearrange the formula and put one calculation into a calculator.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ a^2 &=c^2 – b^2 \\\\ a &= \sqrt{c^2 – b^2} \\\\ x &= \sqrt{20^2 – 11^2}\\\\ x &= 16.70329… \end{aligned} \]

Example 5: checking if a triangle has a right angle

Is the triangle below a right-angled triangle?

Label the sides of the triangle.

If the triangle is a right-angled triangle, then Pythagoras theorem should work:

It is very important to label the hypotenuse (the longest side) correctly with $c$ . The adjacent sides, next to the right angle can be labelled $a$ and $b$ either way around as they are interchangeable.

Write down the formula and apply the numbers.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ 8^2 + 10^2 &= 13^2\\\\ 64+100 &= 169 \\\\ 164 &\neq 169 \end{aligned}\]

Work out the answer.

Pythagoras theorem only works with right-angled triangles.

So because,

\[8^2 + 10^2 \neq 13^2\]

The sides of the triangles do not fit with Pythagoras theorem. Therefore the triangle is NOT a right-angled triangle.

Example 6: checking if a triangle has a right angle

Is the triangle below a right-angled triangle?

Label the sides of the triangle.

If the triangle is a right-angled triangle, then Pythagoras theorem should work:

Write down the formula and apply the numbers.

\[\begin{aligned} a^2 + b^2 &= c^2 \\\\ 6^2 + 8^2 &= 10^2\\\\ 36+64 &= 100 \\\\ 100 &= 100 \end{aligned}\]

This is correct.

Work out the answer.

Pythagoras theorem only works with right-angled triangles.
So because,

\[6^2 + 8^2 = 10^2\]

The sides of the triangles fit with Pythagoras theorem. Therefore the triangle is a right-angled triangle.

Common misconceptions

Make sure you identify the hypotenuse

It is very important to make sure that the hypotenuse is correctly identified and labelled $c$ . You can find the hypotenuse by identifying the side which is opposite the right angle.

Right-angled triangles may be in different orientations

The triangles can be drawn in different orientations.
E.g.

Pythagoras’ Theorem common misconception 1 1

Lengths of sides do not have to be whole numbers

Lengths can be decimals, fractions or even irrational numbers such as surds,

E.g.
$\sqrt{2}$ .

Right-angled triangles

Pythagoras theorem only works on right-angle triangles, however we can sometimes calculate the lengths of other triangles by splitting them into right angled triangles.
E.g.
An isosceles triangle can be made into $2$ right-angled triangles by putting in the line of symmetry.

Pythagoras’ Theorem common misconception 2 1

Pythagoras theorem can also be applied to other shapes

An application of Pythagoras theorem is to extend it to work on other shapes such as a trapezium.

Pythagoras’ Theorem common misconception 3 1

Do not round too early

If you need to use Pythagoras theorem in a question with multiple steps, do not round until the very end of the question or you will lose accuracy. For example, you may need to find the height of a triangle, and then use that height to find its area.

Practice Pythagoras theorem questions

4.9 cm

8.61 cm

4.90 cm

8.60 cm

Practice Pythagoras’ Theorem questions 1 explanation 1

\begin{aligned} a^2 + b^2 &= c^2 \\\\ 7^2 + 5^2 &= x^2 \\\\ x^2 &= 7^2 + 5^2\\\\ x^2 &= 49+25 \\\\ x^2 &= 74\\\\ x &= \sqrt{74}\\\\ x &= 8.602325… \end{aligned}

$x=8.60 cm$ to $2$ decimal places

17.3 cm

17.2 cm

9.7 cm

9.8 cm

Practice Pythagoras’ Theorem questions 2 explanation 1

\begin{aligned} a^2 + b^2 &= c^2 \\\\ 14^2 + 10^2 &= x^2\\\\ x^2 &= 14^2 + 10^2\\\\ x^2 &= 196+10\\\\ x^2 &= 296\\\\ x &= \sqrt{296}\\\\ x &= 17.20465… \end{aligned}

$x=17.2 cm$ to $1$ decimal place.

14.97 cm

14.96 cm

20.59 cm

2.58 cm

Practice Pythagoras’ Theorem questions 3 explanation 1

\begin{aligned} a^2 + b^2 &= c^2 \\\\ x^2 + 10^2 &= 18^2\\\\ x^2+100 &= 324 \\\\ x^2 &= 324 – 100 \\\\ x^2 &= 224\\\\ x &=\sqrt{224}\\\\ x &= 14.96662… \end{aligned}

$x=14.97 cm$ to $2$ decimal places

7.62 cm

6.76 cm

6.75 cm

7.63 cm

Practice Pythagoras’ Theorem questions 4 explanation 1

\begin{aligned} a^2 + b^2 &= c^2 \\\\ x^2 + 2.5^2 &= 7.2^2\\\\ x^2+6.25 &= 51.84 \\\\ x^2 &= 51.84 – 6.25 \\\\ x^2 &= 45.59\\\\ x &=\sqrt{45.59}\\\\ x &= 6.75203… \end{aligned}

$x=6.75 cm$ to $2$ decimal places

No because I measured the angle and it was not $90^{\circ}$

No because $12^2+5^2$ ≠ $13^2$

Yes because I measured the angle and it was $90^{\circ}$

Yes because $12^2+5^2=13^2$

Practice Pythagoras’ Theorem questions 5 explanation 1

\begin{aligned} a^2 + b^2 &= c^2 \\\\ 12^2 + 5^2 &= 13^2\\\\ 144+25 &= 169 \\\\ 169 &= 169 \end{aligned}

This is correct. Pythagoras’ theorem only works with right-angled triangles.

Therefore the triangle is a right-angled triangle.

Yes because $6^2+13^2=14^2$

No because $6^2+13^2$ ≠ $14^2$

Yes because I measured the angle and it was $90^{\circ}$

No because I measured the angle and it was not $90^{\circ}$

Practice Pythagoras’ Theorem questions 6 explanation 1

\begin{aligned} a^2 + b^2 &= c^2 \\\\ 6^2 + 13^2 &= 14^2\\\\ 36+169 &= 196 \\\\ 205 &= 169 \end{aligned}

This is NOT correct. Pythagoras’ theorem only works with right-angled triangles.

Therefore the triangle is NOT a right-angled triangle.

Pythagoras theorem GCSE questions

1. $ABC$ is a right-angled triangle.

Pythagoras’ Theorem GCSE questions 1 1

Calculate the length of $AC.$

Give your answer correct to $3$ significant figures.

(3 marks)

Show answer

7.3^2 + 12.7 ^2 = 214.58

(1)

\sqrt{214.58}

(1)

AC = 14.6485\dots = 14.6 cm

(1)

2. Triangle $ABC$ has a perimeter of $19 cm.$

AB = 5 cm \\

BC = 6 cm

By calculation, deduce whether triangle $ABC$ is a right-angled triangle.

(4 marks)

Show answer

19-(5+6)=8

Third side is $8 cm$ and is the longest so it is the hypotenuse

(1)

5^2 + 6 ^2 = 61

(1)

\sqrt{61}=7.81…

8^2=64

(1)

Triangle $ABC$ is NOT a right-angled triangle

(1)

3. A frame is made from wire

Pythagoras’ Theorem GCSE questions 3 1

The frame is in the shape of a rectangle $10 cm$ by $15$ cm.

The diagonal of the rectangle is also made from wire.

Calculate the total length of wire needed to make the frame and the diagonals.

Give your answer correct to $1$ decimal place.

(4 marks)

Show answer

10^2 + 15 ^2 = 325

(1)

\sqrt{325}=18.02775

(1)

18.02775.. + (2\times 15) + (2\times 10)

(1)

68.027756\dots. = 68.0 cm

(1)

Did you know?

Pythagoras theorem is named after a Greek mathematician who lived about 2500 years ago, however the ancient Babylonians used this rule about 4 thousand years ago! At the same time the Egyptians were using the theorem to help them with right angles when building structures.

Learning checklist

You have now learned how to:

Use Pythagoras theorem to find the length of the longest side of a right-angled triangle – its hypotenuse

Use Pythagoras theorem to find the length of one of the shorter sides of a right-angled triangle

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.