Pyramid

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Faces, edges and vertices Substitution Area of a triangle Area of quadrilaterals How to calculate volume Surface area Pythagoras theorem

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes

Pyramid

Here we will learn about pyramids, including what a pyramid is, how to calculate the volume of a pyramid and how to calculate the surface area of a pyramid.

There are also pyramid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a pyramid?

A pyramid is a three dimensional shape made up of flat faces: a polygon base and triangular lateral faces which meet at a point, called the apex. A triangular pyramid can also be called a tetrahedron, we can have different types of pyramids such as square based pyramids (like the Egyptian Pyramids), pentagonal pyramids, hexagonal pyramids etc. The base of the pyramids does not need to be a regular polygon. The base can be an irregular polygon and if the apex is not over the centre of the polygon, we call the pyramid and oblique pyramid.

Is a cone a pyramid?

A circle is not a polygon as a polygon has a finite number of edges, connected by vertices. As a pyramid has a polygonal base, the base cannot be a circle as a circle is not a polygon. So, a cone is not a pyramid.

However, the volume of a cone is still equal to $V=\frac{1}{3}Bh$ where $B=\pi{r^2}$

To calculate the volume or surface area of a pyramid, we need to know certain lengths within the pyramid. Let’s look at each case separately.

Step-by-step guide: Square based pyramid

See also: Triangular based pyramid

What is a pyramid?

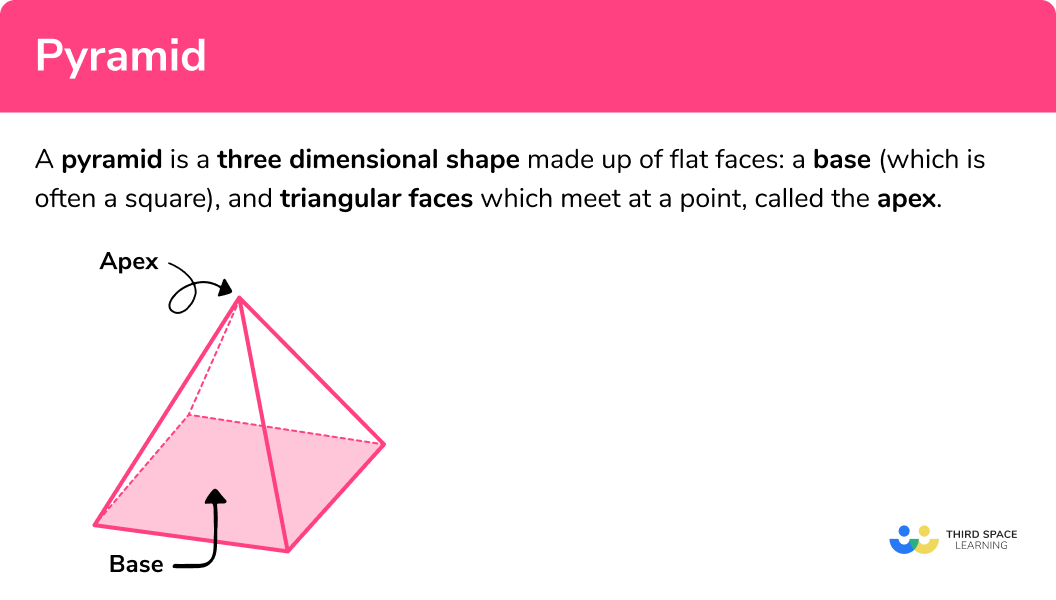
Volume of a pyramid

The formula for the volume of a pyrimad is same no matter if it is a regular pyramid or an irregular pyramid.

To calculate the volume of a pyramid, we use the formula:

V=\frac{1}{3}Bh

where:

$V$ represents the volume of the pyramid,
$B$ represents the area of the base of the pyramid,
$h$ represents the perpendicular height of the pyramid.

This formula can be applied to any pyramid where the base is a polygon.

E.g.

Calculate the volume of the following square based pyramid:

\begin{aligned} V&=\frac{1}{3}\times{B}\times{h}\\\\ &=\frac{1}{3}\times(8\times{8})\times{9}\\\\ &=192\text{ cm}^{2} \end{aligned}

Step-by-step guide: Volume of a pyramid

Surface area of a pyramid

As the area of each triangular face may be different, depending on each side length of the base, the formula for the surface area is a little more tricky to generalise.

However, we can still apply our knowledge of surface area to say:

The surface area of a pyramid is the total sum of the area of each face of the pyramid.

For a square based pyramid, we calculate the area of the base (a square) and the area of four identical triangles:

Note: you may need to calculate the missing length of a triangular side or slant height of the pyramid using Pythagoras’ theorem.

E.g.

Calculate the surface area of the following square based pyramid:

\text{Area of the base }=5\times{5}=25\text{ cm}^{2}

\text{Area of a triangular face }=\frac{1}{2}\times{6}\times{5}=15\text{ cm}^{2}

\text{Surface area }=25+15+15+15+15=25+(4\times{15})=85\text{ cm}^{2}

Step-by-step guide: Surface area of a pyramid

How to calculate the volume of a pyramid

In order to calculate the volume of a pyramid:

Calculate the area of the base.
Substitute values into the formula and solve.
Write the answer, including the units.

How to calculate the volume of a pyramid

Volume and surface area of pyramids worksheet

Get your free pyramid worksheet of 20+ volume and surface area of pyramids questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume and surface area of pyramids worksheet

Get your free pyramid worksheet of 20+ volume and surface area of pyramids questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Pyramid examples

Example 1: volume of a square-based pyramid

Calculate the volume of the square based pyramid below. Write your answer to $2$ decimal places.

Calculate the area of the base.

The area of the base is:

\begin{aligned} &5.2\times 5.2={5.2}^2=27.04 \\\\ &B=27.04cm^2 \end{aligned}

2Substitute values into the formula and solve.

The formula for the volume of a pyramid is: $V=\frac{1}{3}Bh$ with $B=27.04cm^2$ and $h=6.8cm$ . Substituting these values for the base and the vertical height, we have:

\begin{aligned} V&=\frac{1}{3}\times{27.04}\times{6.8}\\\\ V&=61.29066667… \end{aligned}

3Write the answer, including the units.

V=61.29\text{ cm}^{3}\text{ (2dp)}

Step-by-step guide: Volume of square based pyramid

Example 2: volume of a rectangular-based pyramid

The pyramid ABCDE has a rectangular base. The apex is vertically above the centre of the base. Calculate the volume of the pyramid, correct to $1$ decimal place.

Calculate the area of the base.

The area of the base is:

$\begin{aligned} &6.8\times 7.2=48.96 \\\\ &B=48.96cm^2 \end{aligned}$

Substitute values into the formula and solve.

The formula for the volume of a pyramid is $V=\frac{1}{3}Bh$ , where $B=48.96cm^2$ and $h=8.1cm$ . Substituting these values into the formula, we have

$\begin{aligned} V&=\frac{1}{3}\times{48.96}\times{8.1}\\\\ V&=132.192 \end{aligned}$

Write the answer, including the units.

V=132.2\text{ cm}^{3}\text{ (1dp)}

Example 3: calculating the height, given the volume

Find the height of a pyramid with volume $48 \ cm^3$ and base area $15 \ cm^2$ .

Calculate the area of the base.

We already know that the area of the base is $15 \ cm^2$ , so we can move on to step $2$ .

Substitute values into the formula and solve.

We need to use the formula for the volume of a pyramid and solve it to find the value of the height, $h$ .

$\begin{aligned} V&=\frac{1}{3}\times{B}\times{h}\\\\ 48&=\frac{1}{3}\times{15}\times{h}\\\\ 48&=5h\\\\ h&=9.6 \end{aligned}$

Write the answer, including the units.

$h=9.6cm$ .

How to calculate the surface area of a pyramid

In order to calculate the surface area of a pyramid:

Calculate the area of the base.
Calculate the area of all of the triangular faces.
Calculate the total surface area.
Write the answer, including the units.

How to calculate the surface area of a pyramid

Surface area of a pyramid examples

Example 4: finding the surface area from a 3D diagram

The polyhedron $ABCDE$ is a square based pyramid. The point $M$ lies on the edge $AD$ where $AM=MD$ . The point $E$ is perpendicular to the centre of the base $ABCD$ .

Calculate the surface area of the pyramid.

Calculate the area of the base.

The area of the base is:

$5\times 5=5^2=25$

Calculate the area of all of the triangular faces.

The triangular face AED has a height of 7cm, and a width of 5cm. The area of a triangle is $A=\frac{1}{2}\times{b}\times{h}$ , so the area of $AED$ is:

$\begin{aligned} A&=\frac{1}{2}\times{b}\times{h} \\\\ &=\frac{1}{2}\times{5}\times{7} \\\\ &=17.5\text{ cm}^{2} \end{aligned}$

Each triangular face for a square based pyramid is congruent when the apex is directly above the centre of the base. This means that we can calculate the area of one of the triangular faces, then multiply the solution by $4$ to calculate the area of all four triangles.

$17.5\times{4}=70\text{ cm}^{2}$

Calculate the total surface area.

The surface area ( $SA$ ) of the pyramid is the total sum of the area of each face, giving us:

$SA=25+70=95$

Write the answer, including the units.

SA=95\text{ cm}^{2}

Example 5: finding the surface area from a 3D diagram

$ABCD$ is a triangular based pyramid.

Triangle $ABC$ is equilateral. All of the other faces are congruent, isosceles triangles.

The point $M$ is the midpoint of the line $AC$ such that:

$MB=3\sqrt{3}\text{ cm}$
$MC=3\text{ cm}$
$MD=8\text{ cm}.$

Calculate the surface area of the pyramid. Write your answer in the form $a+b\sqrt{c}\text{ cm}^{2}$ where $a, \ b,$ and $c$ are integers to be found.

Calculate the area of the base.

The area of the base (which is a triangle) is:

$\begin{aligned} A&=\frac{1}{2}\times{b}\times{h}\\\\ &=\frac{1}{2}\times{6}\times{3\sqrt{3}}\\\\ &=9\sqrt{3} \end{aligned}$

Calculate the area of all of the triangular faces.

The remaining three triangular faces are all the same as stated in the question (they are congruent). This means that we can calculate the area of one of the faces, and then multiply it by $3.$

The triangle $ACD$ has a height of $8cm$ , and a width of $6cm$ (double $3cm$ ).

The area of triangle $ACD$ is therefore equal to

$\begin{aligned} A&=\frac{1}{2}\times{b}\times{h}\\\\ &=\frac{1}{2}\times{8}\times{6}\\\\ &=24\text{ cm}^{2} \end{aligned}$

Calculate the total surface area.

The total surface area is the sum of each of the four triangles:

$9\sqrt{3}+3\times 24$

Write the answer, including the units.

As the question asks us to write the solution in the form $a+b\sqrt{c}\text{ cm}^{2}$ , we have:

$SA=72+9\sqrt{3}\text{ cm}^{2}$

Example 6: finding the surface area from a net

Calculate the surface area of the pyramid. Give your answer correct to 2 decimal places.

Calculate the area of the base.

The area of the square base is:

$7\times 7=7^2=49$

Calculate the area of all of the triangular faces.

We need to add the area of the base to the area of the triangular faces.

There are $4$ triangular faces.

First we need to find the height, $h$ , of one of the triangles using Pythagoras theorem.

h=\sqrt{9^{2}-3.5^{2}}=8.291561976...

Now that we know the height of a triangular face, the area of the same triangular face is:

$\begin{aligned} A&=\frac{1}{2}\times{7}\times{8.291561976}\\\\ &=29.02046692 \end{aligned}$

The area of all four triangular faces is therefore:

$29.02046692\times{4}=116.0818677.$

Notice that we have not rounded any solution so far (we leave this until the very last line of calculation).

Calculate the total surface area.

The total surface area of the net is:

$49+116.0818677=165.0818677$

Write the answer, including the units.

SA=165.08\text{ cm}^{2}\text{ (2dp)}

Common misconceptions

Use the perpendicular height

The height of the shape needs to be the perpendicular height. To find the volume of the pyramid we use its perpendicular height. To find the area of a triangular face we use the perpendicular height of the triangular face. It is also common to confuse the volume of a pyramid with the volume of a prism. It is important to know the difference between 3D shapes.

Surface area has square units

The surface area will have square units such as square centimetres ( $cm^2$ ) or square metres ( $m^2$ ).

Volume has cube units

The volume will have cube units such as cubic centimetres ( $cm^3$ ) or cubic metres ( $m^3$ ).

Be accurate

When there are two or more steps in your workings, do not round your workings. Only round at the end of your solution so that your answer is accurate.

Take care with rounding

At the end of the question, make sure you round your answer to the correct number of decimal places or significant figures.

Practice pyramid questions

648.03cm^3

1944.08cm^3

972.04cm^3

112.70cm^3

\begin{aligned} V&=\frac{1}{3}\times{B}\times{h}\\\\ &=\frac{1}{3}\times{11.5^2}\times{14.7}\\\\ &=648.025\\\\ &=648.03\text{ cm}^{3}\text{ (2dp)} \end{aligned}

630\text{ cm}^3

210\text{ cm}^3

1890\text{ cm}^3

5670\text{ cm}^3

\begin{aligned} V&=\frac{1}{3}\times{B}\times{h}\\\\ &=\frac{1}{3}\times{(15\times{18})}\times{21}\\\\ &=1890\text{ cm}^{3} \end{aligned}

4\text{ cm}

10\text{ cm}

8\text{ cm}

12\text{ cm}

\begin{aligned} V&=\frac{1}{3}\times{B}\times{h}\\\\ 160&= \frac{1}{3} \times 40 \times h\\\\ 480&=40\times h\\\\ h&=12\text{ cm} \end{aligned}

48 \text{ cm}^2

128 \text{ cm}^2

80 \text{ cm}^2

64 \text{ cm}^2

\begin{aligned} &\text{Base }=4\times{4}=16\text{ cm}^{2}\\\\ &\text{Triangular faces }=(\frac{1}{2}\times{8}\times{4})\times{4}=64\text{ cm}^{2} \\\\ &SA=16+64=80\text{ cm}^{2} \end{aligned}

61.4 \text{ cm}^2

68.89 \text{ cm}^2

157.7 \text{ cm}^2

246.5 \text{ cm}^2

\begin{aligned} SA&=(4.15\times{2})^{2}+(\frac{1}{2}\times{10.7}\times{8.3})\times{4}\\\\ &=68.89+177.62\\\\ &=246.51\text{ cm}^{2}\text{ (2dp)} \end{aligned}

60\text{ cm}^2

84\text{ cm}^2

66\text{ cm}^2

51\text{ cm}^2

First we need to find the height of the triangular face.

h=\sqrt{5^{2}-3^{2}}=4\text{ cm}

\begin{aligned} SA&=6^{2}+(\frac{1}{2}\times{6}\times{4})\times{4}\\\\ &=36+48\\\\ &=84\text{ cm}^{2} \end{aligned}

Pyramid GCSE questions

1. A square-based pyramid has a base with side $15 \ cm.$

The perpendicular height of the pyramid is $20 \ cm.$

Calculate the volume of the pyramid.

(2 marks)

Show answer

\frac{1}{3}\times 15^2 \times 20

(1)

1500

(1)

2. The diagram shows a square-based pyramid.

Pyramid GCSE Question 2

Calculate the surface area of the pyramid.

(3 marks)

Show answer

\frac{1}{2}\times 4.3 \times 6.8=14.62

(1)

4.3^2+4\times 14.62

(1)

76.97

(1)

3. A solid is made from a pyramid on top of a cuboid. $AD=12m,CD=10m, CH=9m$ . $M$ and $N$ are midpoints of the lines $EH$ and $EF$ respectively with $IM=8m,$ and $IN=\sqrt{53}m.$

Calculate the surface area of the shape. Write your answer to $2$ decimal places.

(4 marks)

Show answer

\frac{1}{2}\times 10\times 8\times {2}= 80

(1)

\frac{1}{2}\times 12\times \sqrt{53}\times {2}=12\sqrt{53}

(1)

2(12\times{9})+2(10\times{9})+(12\times{10})=516

(1)

516+12\sqrt{53}+80=683.36\text{ m}^{2}\text{ (2dp)}

(1)

Learning checklist

You have now learned how to:

Calculate surface areas and volumes of pyramids

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.