GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Polygons Types of quadrilaterals Triangles 3D shapes Adding and subtracting negative numbersThis topic is relevant for:

Faces, Edges And Vertices
Here we will learn about faces, edges and vertices including how to calculate the number of vertices, edges and faces of a 3D shape, and how to classify polyhedrons given the number of faces, edges and vertices.
There are also faces, edges and vertices worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are faces, edges and vertices?
Faces, edges and vertices are features of a 3D shape.
- Faces are flat surfaces on the shape.
- Edges are straight lines that define the sides of the polygons that make up each face of the shape.
- Vertices (or corners) are points where at least three edges meet.
To calculate the number of faces, edges and vertices of a 3D shape, we need to count the number of each using the 3D object.
Note, you need to be able to visualise the 3D object, you may not be given the shape to help you.
For example, a cube has 6 vertices, 12 edges and 6 faces.
| Vertex | Edge | Face |
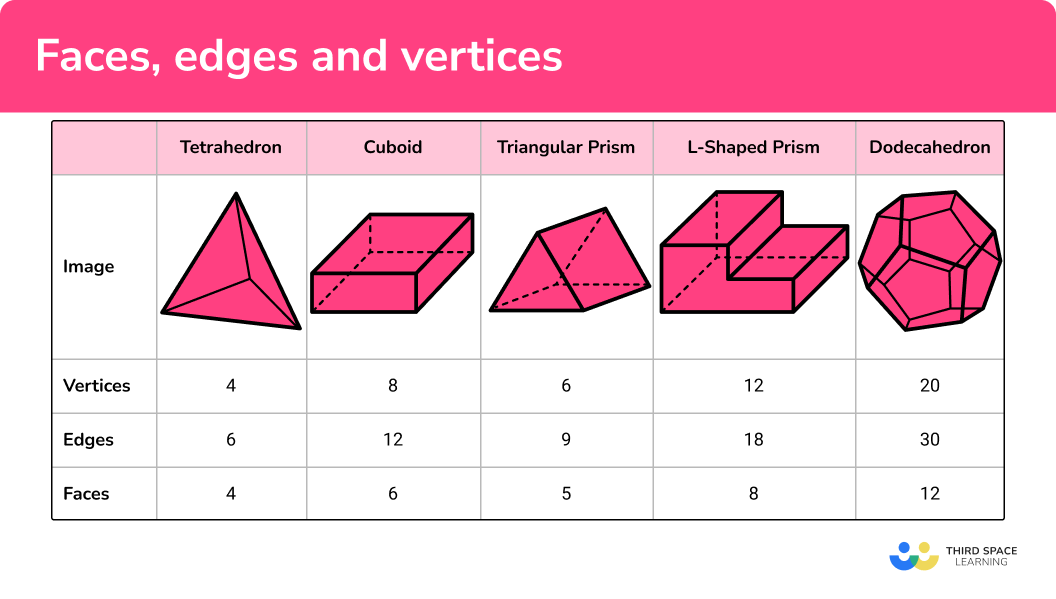
There are several 3D shapes that we need to know the number of vertices, edges and faces of.
Below is a diagram of common 3D shapes (split into polyhedra and non-polyhedra) along with the number of vertices, edges and faces.
E.g. Polyhedrons – flat faces, straight edges and sharp vertices.
| Tetrahedron | Cuboid | Triangular prism | L-shaped prism | Dodecahedron | |
| Image | |||||
| Vertices | 4 | 8 | 6 | 12 | 20 |
| Edges | 6 | 12 | 9 | 18 | 30 |
| Faces | 4 | 6 | 5 | 8 | 12 |
E.g. Non-polyhedra – don’t have flat faces, straight edges and sharp vertices.
| Sphere | Cone | Cylinder | Frustum | Taurus | |
| Image | |||||
| Vertices | 0 | 1 | 0 | 0 | 0 |
| Edges | 0 | 1 | 2 | 2 | 0 |
| Faces | 1 | 2 | 3 | 3 | 1 |
What are faces, edges and vertices?

Platonic solids
Some of the most famous polyhedra are called the Platonic solids named after the Greek philosopher and Mathematician, Plato. Each of the Platonic solids can be inscribed inside a sphere as they are considered to be regular 3D polyhedra.
The number of faces determines the name of the polyhedron:
| Platonic solid | Image |
| Tetrahedron 4 vertices 6 edges 4 faces Each face is an equilateral triangle | |
| Cube 8 vertices 12 edges 6 faces Each face is a square | |
| Octahedron 6 vertices 12 edges 8 faces Each face is an equilateral triangle | |
| Dodecahedron 20 vertices 30 edges 12 faces Each face is a regular pentagon | |
| Icosahedron 12 vertices 30 edges 20 faces Each face is an equilateral triangle |
What are faces, edges and vertices?
How to calculate the number of faces, edges and vertices
In order to calculate the number of faces, edges and vertices of a 3D shape:
- Inspect the shape to visualise its faces / edges / vertices.
- Count the number of faces / edges / vertices.
In order to count the number of faces, edges and vertices of a 3D shape:
- Recall that a face is a flat surface and count the faces systematically going around the 3D shape. (TIPS: For prisms and pyramids imagine/sketch the net of the shape . For some of the platonic solids the number of faces is linked to the name of the shape.)
- Recall that an edge is a straight line where two faces meet and count the edges systematically going around and between the faces. (TIPS: Be careful not to count the same edge twice.)
- Recall that vertices are the corners of a 3D shape where 3 or more edges meet and count them systematically going around the shape.
*If there is an image of the 3D shape, note that some faces, edges and vertices may be hidden in the 2D representation.
How to calculate the number of faces, edges and vertices

Faces edges and vertices worksheet

Get your free faces edges and vertices worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Faces edges and vertices worksheet

Get your free faces edges and vertices worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on 3D shapes
Faces, edges and vertices is part of our series of lessons to support revision on 3D shapes. You may find it helpful to start with the main 3D shapes lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Faces, edges and vertices examples
Example 1: cuboid
Below is a cuboid.
Calculate the number of vertices for the polyhedron.
- Inspect the shape to visualise its faces / edges / vertices.
A vertex is a corner where at least 2 edges meet.
2Count the number of faces / edges / vertices.
A cuboid has 8 vertices.
Example 2: triangular prism
A triangular prism has 5 faces and 6 vertices.
Calculate the number of edges of the polyhedron.
- Inspect the shape to visualise its faces / edges / vertices.
An edge is a straight line that connects two vertices.
2Count the number of faces / edges / vertices.
The triangular prism has 9 edges.
Example 3: dodecahedron
A dodecahedron has 12 faces and 30 edges.
Calculate the number of vertices for the polyhedron.
- Inspect the shape to visualise its faces / edges / vertices.
A vertex is a corner where at least 2 edges meet.
2Count the number of faces / edges / vertices.
A dodecahedron has 20 vertices.
Example 4: cone
Below is a cone.
Calculate the number of faces for the cone.
- Inspect the shape to visualise its faces / edges / vertices.
A face is surrounded by vertices and edges.
2Count the number of faces / edges / vertices.
A cone has 2 faces.
Example 5: möbius strip
A Möbius strip has 1 face and 0 vertices.
How many edges does it have?
- Inspect the shape to visualise its faces / edges / vertices.
An edge surrounds the face of a polyhedron.
2Count the number of faces / edges / vertices.
Look at this shape very carefully. Trace the edge, starting at 1 .
The Möbius strip has one edge.
Example 6: cylinder
A cylinder has 3 faces and 0 vertices.
Calculate the number of edges for the polyhedron.
- Inspect the shape to visualise its faces / edges / vertices.
An edge surrounds the face of a polyhedron.
2Count the number of faces / edges / vertices.
Be careful here. The vertical sides of the cylinder are not edges, they just show the curved face of the cylinder.
A cylinder has 2 edges.
Common misconceptions
- Incorrect values for a property
A possible error is that the incorrect number of faces, edges or vertices is calculated.
E.g.
The number of vertices for a cube is calculated as 8 whereas a cube has 6 vertices.
- Incorrect property
A possible error is that the faces, edges and vertices are mixed up and the wrong one is calculated.
E.g.
The number of edges is counted on a shape instead of the number of faces.
Practice faces, edges and vertices questions
1. A cube has 6 faces and 8 vertices.
Calculate the number of edges for the polyhedron.




Counting the number of edges, we have
4 vertical edges + 8 horizontal edges = 12 edges
2. An icosahedron has 12 vertices and 30 edges.
Use the fact that V-E+F=2 to calculate the number of faces for the polyhedron where V is the number of vertices, E is the number of edges and F is the number of faces of the polyhedron.




3. An octagonal pyramid has 9 faces and 9 vertices.
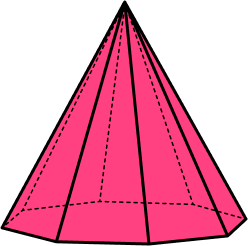
Calculate the number of edges for the polyhedron.




The base has 8 edges as it is an octagon. Each vertex is joined to the apex and so 8+8=16 edges.
4. An L-shaped prism has 12 vertices and 18 edges.
Calculate the number of faces for the prism.




Count each face separately, remember the front and the back faces.
5. A hexagonal pyramid has 12 edges and 7 vertices.
Calculate the number of faces of the polyhedron.




Count each face separately, remember the base of the pyramid
6. How many vertices does a sphere have?




A sphere does not have any vertices.
Faces, edges, and vertices GCSE questions
1. The trapezoidal prism below has a constant cross section. The front face has 4 sides, and all the adjacent faces are rectangles. Calculate the difference between the number of vertices and the number of faces for the prism.
(3 marks)
Number of vertices = 8
(1)
Number of faces = 6
(1)
8-6=2(1)
2. (a) The frustum below is made from slicing a cone horizontally, removing the top part of the cone.
Determine the number of faces for the frustum.
(b) The formula for the volume of a cone is equal to V=\frac{1}{3}\pi{r}^{2}h . If the radius of the base of the frustum is equal to 3cm and the height of the original cone is 5cm , calculate the volume of the cone. Write your answer to 1 decimal place. State the units.
(4 marks)
(a)
3
(1)
(b)
V=\frac{1}{3}\pi\times {3}^{2}\times 5
(1)
V=47.1(1)
cm^3(1)
3. (a) Two cuboids are placed together to form an L-shaped prism. The front and back faces are flat, congruent, 2D shapes. Calculate the number of vertices, edges and faces of the new prism.
(b) Calculate the value of V-E+F if:
- V represents the number of vertices
- E represents the number of edges
- F represents the number of faces.
(4 marks)
(a)
Vertices = 12
(1)
Edges = 18
(1)
Faces = 8
(1)
(b)
12-18+8=2
(1)
Learning checklist
You have now learned how to:
-
Identify and describe the properties of 3-D shapes, including the number of edges, vertices and faces
The next lessons are
Interesting 3D shapes
There are a range of 3D shapes that are mathematically interesting.
Below is a diagram of a Möbius strip:
The Möbius strip is a continuous loop with one edge and one face. Imagine tracing a line around the loop. The start point would also be the end point, yet the line appears to exist on “both sides” of the Möbius strip.
Another interesting 3D shape is the standard football. The 3D shape is based on a truncated icosahedron with 12 pentagons and 20 hexagons. The shape has 90 edges and 60 vertices. Below is an example of the net of a truncated icosahedron.
Euler’s polyhedra formula
For a polyhedron to be classified as a cube, a dodecahedron or a tetrahedron for example, we can use Euler’s polyhedra formula to calculate the number of vertices, edges or faces of the shape:
V-E+F=2
where F is the number of faces, V the number of vertices, and E the number of edges of a polyhedron. This means that if you know two of the three characteristics of the polyhedron, you can calculate the missing value.
E.g. We know that a cube has 4 vertices and 4 faces:
Substituting these values into the formula, we get:
So a cube has 6 edges.
This is only for polyhedrons.
The Euler characteristic
So far, we have looked at V-E+F=2 for any convex polyhedron including the Platonic solids. However, this is not true for all polyhedra. The Euler characteristic is the value of the expression V-E+F , so for a cube, the Euler characteristic is 2 . We represent the Euler characteristic using the symbol, so we can say for any polyhedra:
V-E+F=\chi
For example, a sphere has the following features: V=0, E=0, F=1 .
The Euler characteristic for a sphere is:
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.