One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Multiplying fractions Substitution Area of a circle RoundingThis topic is relevant for:
Sphere
Here we will learn about spheres, including how to find the volume and surface area of a sphere.
There are also sphere worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a sphere shape?
A sphere shape is a three dimensional shape where every point of its surface is equidistant (the same distance) from the centre of the sphere. The distance from the centre of a sphere to its surface is called the radius. A sphere has no vertices.
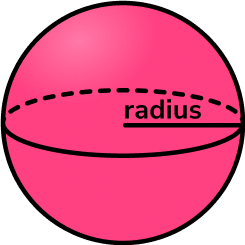
A hemisphere is half a sphere.
What is a sphere shape?
Volume of a sphere shape
The volume of a sphere is the amount of space there is inside a sphere.
The formula for the volume of a sphere is:
\text{Volume}=\frac{4}{3}\pi{r}^3E.g. Find the volume of the sphere
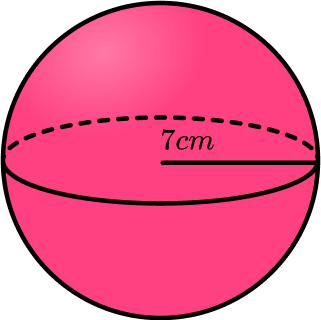
This sphere has a radius of 7 \; cm .
\begin{aligned} \text{Volume}&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 7^3\\\\ &=\frac{1372}{3}\pi\\\\ &=1436.755... \\\\ &=1440 \ cm^3 \ \text{(3sf)} \end{aligned}Step-by-step guide: Volume of a sphere (coming soon)
Surface area of a sphere shape
The surface area of a sphere is the area which covers the outer surface of a sphere.
The formula for the surface area of a sphere is:
\text{Surface Area}=4 \pi r^2E.g. Find the surface area of the sphere
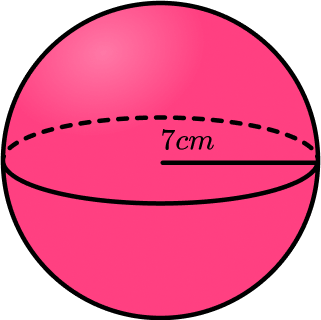
This sphere has a radius of 7 \; cm .
\begin{aligned} \text{Surface area}&=4\pi r^2\\\\ &=4 \times \pi \times 7^2\\\\ &=196\pi\\\\ &=615.752...\\\\ &=616 \ cm^2 \ \text{(to 3 sf)} \end{aligned}Step-by-step guide: Surface area of a sphere
How to calculate the volume or surface area of a sphere
In order to calculate the volume of a sphere or the surface area of a sphere:
- Write down the formula.
- Substitute the given values.
- Work out the calculation
- Write the final answer.
How to calculate the volume or surface area of a sphere
Sphere shape worksheet
Get your free sphere shape worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE Sphere shape worksheet
Get your free sphere shape worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREESphere shape examples
Example 1: volume of a sphere
Calculate the volume of a sphere of radius 12 \; cm. Give your answer to 3 significant figures.
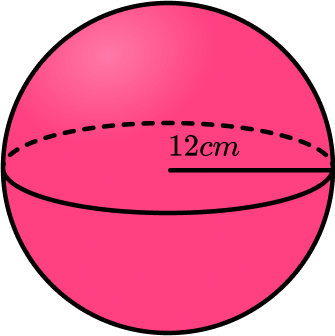
- Write down the formula for the volume of a sphere.
2Substitute the given values into the formula.
V=\frac{4}{3} \times \pi \times 12^33Complete the calculation.
\begin{aligned} &=2304\pi \\\\ &=7238.229... \end{aligned}4Write the final answer, including the units.
The radius is given in centimetres so the volume will be cubic centimetres.
The volume of the sphere is 7240 \; cm^3 (3 sf) .
Example 2: volume of a sphere, given the diameter
Calculate the volume of a sphere with a diameter of 30 \; cm . Write your answer in terms of \pi .
Write down the formula for the volume of a sphere.
Substitute the given values into the formula.
The diameter is twice the length of the radius. To calculate the radius, we need to first divide the diameter by 2:
30 \div 2=15 \; cm
The radius is 15 \; cm. Substituting this into the formula for the volume of a sphere, we have
V=\frac{4}{3} \times \pi \times 15^3
Complete the calculation.
Write the final answer, including the units.
The radius is given in centimetres so the volume will be cubic centimetres.
The volume of the sphere is 4500\pi \; cm^3 .
Example 3: volume of a hemisphere
Calculate the volume of a hemisphere of radius 4 \; cm . Write your answer to 2 decimal places.
Write down the formula for the volume of a sphere.
Substitute the given values into the formula.
Complete the calculation.
But this is for a whole sphere. We need a hemisphere, so we need to divide by 2.
268.0825…\div 2=134.041...
Write the final answer, including the units.
The radius is given in centimetres so the volume will be cubic centimetres.
The volume of the hemisphere is 134.04 \; cm^3 \; (to \; 2 dp).
Example 4: surface area of a sphere
Calculate the surface area of a sphere with radius 7 \; cm . Write your answer to 1 decimal place.
Write down the formula for the surface area of a sphere.
Substitute the given values into the formula.
Here we know the radius of the sphere is 7 \; cm so we substitute r=7 into the formula for the surface area.
SA=4\times\pi\times{7}^{2}
Complete the calculation.
Write the final answer, including the units.
The radius is measured in centimetres so the surface area is measured in square centimetres (cm^2) , with the solution rounded to 1 decimal place.
The surface area of the sphere is 615.8 \; cm^2 .
Example 5: surface area of a sphere given the diameter – in terms of π
Find the surface area of a sphere with the diameter of 20 \; cm. Leave your answer in terms of \pi .
Write down the formula for the surface area of a sphere.
Substitute the given values into the formula.
The diameter of the sphere is 20\;cm and so we need to use this to calculate the radius and hence the surface area of the sphere.
20 \div 2=10
The radius of the sphere is 10\;cm.
We now know the radius of the sphere is 10\;cm so we substitute r=10 into the formula for the surface area.
SA=4\times\pi\times{10}^{2}
Complete the calculation.
Write the final answer, including the units.
The radius is measured in centimetres so the surface area is measured in square centimetres (cm^2) , with the solution in terms of \pi .
The surface area of the sphere is 400\pi \;cm^2 .
Example 6: total surface area of a hemisphere
Find the total surface area of a hemisphere with a radius 4 \; cm. Write your answer to 3 significant figures.
Write down the formula for the surface area of a sphere.
For the surface area of a hemisphere we need half of the surface area of a sphere and add it on to the area of the flat circular base. The formula can be adapted.
\text{Total Surface Area}=\frac{1}{2}\times 4\pi r^2 + \pi r^2
Substitute the given values into the formula.
Complete the calculation.
Write the final answer, including the units.
The radius is measured in centimetres so the surface area is measured in square centimetres (cm^2) , with the solution rounded to 3 significant figures.
The surface area of the sphere is 151 \; cm^2 \; (to \; 3 sf) .
Common misconceptions
- Using the correct formula
There are several formulas that can be used, so we need to match the correct formula to the correct context.
- Rounding
It is important to not round the answer until the end of the calculation. This will mean your final answer is accurate.
- Make sure you have the correct units
For area we use square units such as cm^2, m^2, km^2.
For volume we use cube units such as cm^3, m^3, km^3.
- Using the radius or the diameter
It is a common error to mix up radius and diameter. Remember the radius is half of the diameter.
Practice sphere shape questions
1. Find the volume of a sphere with radius 4.3 \; cm. Write your answer to 2 decimal places.
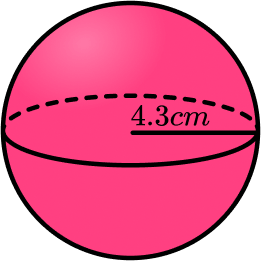
We are finding the volume of a sphere so we substitute the value of the radius r=4.3 into the formula V=\frac{4}{3}\pi{r}^{3}
\begin{aligned} \text{Volume}&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 12^3\\\\ &=333.0381428… \\\\ &=333.04\text{cm}^{3} \ \text{(2dp)} \end{aligned}
2. Find the volume of a sphere with radius 18 \; cm. Leave your answer in terms of \pi .
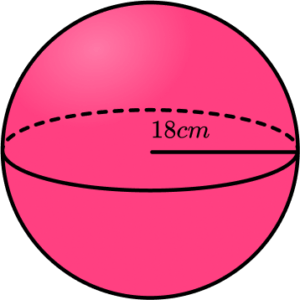
We are finding the volume of a sphere so we substitute the value of the radius into the formula V=\frac{4}{3}\pi{r}^{3} . As the diameter is twice the length of the radius, r=36 \div 2=18 \;cm.
\begin{aligned} \text{Volume}&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 18^3\\\\ &=7776\pi \\\\ &=7776\pi \; cm^3 \end{aligned}
3. Find the volume of a hemisphere with radius 6.2 \; cm. Write your answer to 1 decimal place.
We are finding the volume of a hemisphere, so we need to calculate half of the volume of a sphere using the radius r=6.2 \; cm, and the formula: V=(\frac{4}{3}\pi{r}^3)\div{2}.
\begin{aligned} V&=(\frac{4}{3}\pi{r}^3)\div{2}\\\\ &=(\frac{4}{3}\times\pi\times{6.2}^3)\div{2}\\\\ &=499.152996…\\\\ &=499.2\text{ cm}^3 \end{aligned}
4. Find the surface area of a sphere with radius 4.6 \; cm. Give your answer to 2 decimal places.
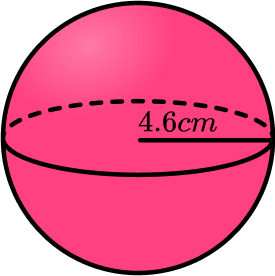
We are finding the surface area of a sphere, so we substitute the value of the radius r=4.6 into the formula SA=4\pi r^2.
\begin{aligned} \text{Surface area}&=4\pi r^2\\\\ &=4 \times \pi \times 4.6^2\\\\ &=265.9044022…\\\\ &=265.90 \text{ cm}^2 \ \text{(2dp)} \end{aligned}
5. Find the surface area of a sphere with a diameter of 16 \; mm. Leave your answer in terms of \pi.
We are finding the surface area of a sphere, so we need to calculate the value of the radius using the diameter, then substitute the value of the radius into the formula for the surface area.
r=16 \div 2=8 \; mm
The radius r=8 \; mm.
\begin{aligned} \text{Surface area}&=4\pi r^2\\\\ &=4 \times \pi \times 8^2\\\\ &=256\pi \ \text{mm}^2 \end{aligned}
6. Find the surface of a hemisphere with radius 7.8 \; cm. Give your answer to 1 decimal place.
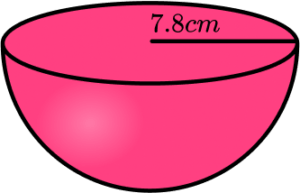
We need to find the curved surface area by finding half of the surface area of a sphere. Then we add on the area of the circular top.
\begin{aligned} \text{Total surface area}&=3\pi r^2\\\\ &=3 \times \pi \times{7.8}^2\\\\ &=573.4034911…\\\\ &=573.4 \text{ cm}^2 \ \text{(1dp)} \end{aligned}
Sphere shape GCSE questions
1. Here is a sphere with a radius 8.4 \; cm.
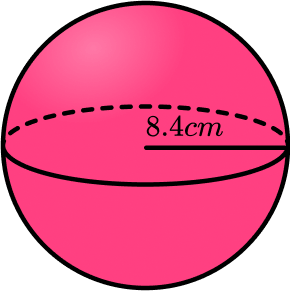
Calculate the volume of the sphere.
Write your answer to 1 decimal place.
(2 marks)
(1)
2482.71271…=2482.7 \; cm^3
(1)
2. A tennis ball has a radius of 3.4 \; cm. Each tennis ball is covered in felt. Calculate the area of the felt required to cover the ball to the nearest square millimetre.
(4 marks)
(1)
SA=4\times \pi \times{34}^2
(1)
14526.72443…
(1)
14527 \; mm^2
(1)
3. A container is a hemisphere with a diameter of 70 \; cm.
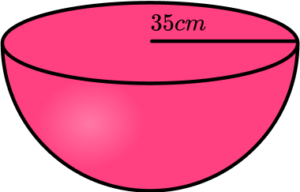
Sand fills the container at a rate of 5000 \; cm^3 per minute.
How long does it take to fill the container?
Give your answer to the nearest minute.
(3 marks)
(1)
89797.19002… \div{5000}=17.959438…
(1)
17.959438… = 18 minutes
(1)
4. A sphere has a surface area of 1000 \; m^2.
Calculate its volume.
Give your answer to 3 significant figures.
(3 marks)
(1)
\frac{4}{3}\times \pi \times8.920620581^3=2973.540194…
(1)
2973.540194…=2970 \; m^3 \; (3sf)
(1)
Learning checklist
You have now learned how to:
- Find the volume of a sphere
- Find the surface area of a sphere
- How to solve problems involving spheres
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths revision programme.