Area of a circle

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Parts of a circle

Irrational numbers

Rounding decimals

Rounding to significant figures

This topic is relevant for:

GCSE Maths Geometry and Measure Area

Area Of A Circle

Here we will learn about calculating the area of a circle including how to calculate the area of a circle given the radius, how to calculate the area of a circle given the diameter and how to calculate the area of a circle given the circumference.

There are also area of a circle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

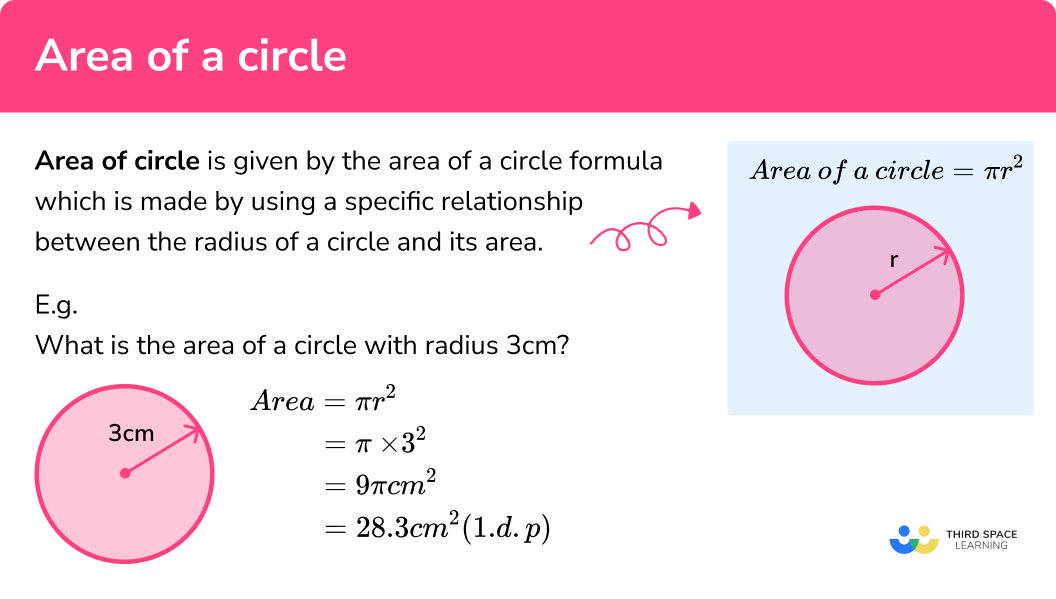
What is the area of a circle?

The area of a circle is given by the area of a circle formula which is made by using a specific relationship between the radius of a circle and its area.

Area of a circle formula:

\pi \times r\times r

we usually simplify this to

E.g.
What is the area of a circle with radius $3cm$ ?

\begin{aligned} \text { Area } &=\pi r^{2} \\\\ &=\pi \times 3^{2} \\\\ &=9 \pi \mathrm{cm}^{2} \\\\ &=28.3 \mathrm{~cm}^{2}(1 . \mathrm{d} . \mathrm{p}) \end{aligned}

What is the area of a circle?

What is pi?

$\pi$ (pronounced pi) represents the ratio of the circumference of a circle to its diameter.
For all circles if you divide the length of the circumference by the length of the diameter you get the value $\pi$ .

Note: $\pi$ is an irrational number which means it cannot be written as a fraction. It is a non recurring decimal and has an approximate value of $3.14159\dots$

In GCSE you should use the $\pi$ button on your Casio calculator when working with $\pi$ .
To get this you need to press [SHIFT][ $\times 10^x$ ].
Alternatively you can use the value $3.142$ instead.

Sometimes a question may ask you to leave an answer in terms of pi
E.g
$6 \times \pi = 6\pi$ (this is an answer in terms of pi)

$8 \times \pi = 8\pi$ (this is an answer in terms of pi)

$10 \times \pi = 31.41...$ (this is an answer not in terms of pi)

How to calculate the area of a circle

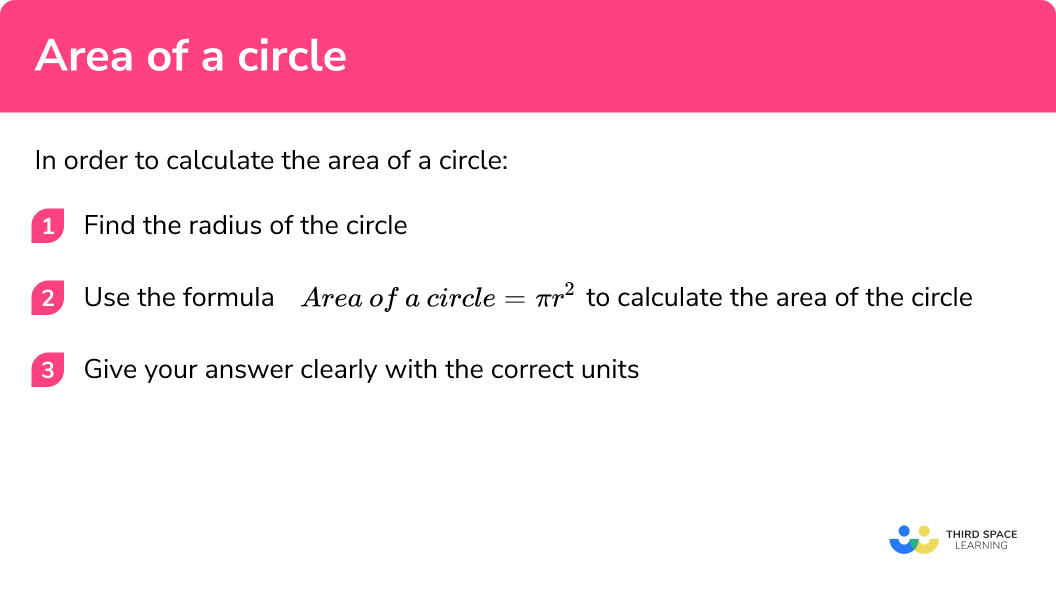
In order to calculate the area of a circle:

Find the radius of the circle.
Use the formula $\text{Area of a circle} = \pi r^2$ to calculate the area of the circle.
Give your answer clearly with the correct units.

Explain how to calculate the area of a circle

Area of a circle worksheet

Get your free area of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area of a circle worksheet

Get your free area of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area of a circle examples

Example 1: calculating the area of the circle given the radius

A circle has a radius of $6cm$ , calculate its area.
Give your answer to $2dp$ .

Find the radius of the circle.

The radius is given in the question

Radius $=6cm$

2Use the formula $\pi r^2$ to calculate the area of the circle.

\begin{aligned} &\pi r^2\\\\ &= \pi \times r\times r\\\\ &= \pi \times6\times 6\\\\ &= 36\pi \\\\ &= 113.0973355... \end{aligned}

3Give your answer clearly with the correct units.

Remember the question asks you to round your answer to ‘2 decimal places’

113.10cm^2

Example 2: calculating the area of the circle given the diameter

A circle has a diameter of $10mm.$ , calculate its area.
Give your answer to $1dp$ .

Find the radius of the circle.

In this question the question gives you the diameter. You need the radius to find the area of the circle.

Remember the diameter of the circle is twice the radius.

Diameter $= 10mm$

Radius $=10mm \div 2$

Radius $= 5mm$

Use the formula $\pi r^2$ to calculate the area of the circle.

\begin{aligned} &\pi r^2\\\\ &= \pi \times r\times r\\\\ &= \pi \times5\times 5\\\\ &= 25\pi \\\\ &=78.53981... \end{aligned}

Give your answer clearly with the correct units.

Remember the question asks you to round your answer to ‘1 decimal place’

$78.5mm^2$

Example 3: calculating the area of the circle, given the radius, answer in terms of 𝝅

A circle has a radius of $8m.$ , calculate its area.
Give your answer in terms of $\pi$ .

Find the radius of the circle.

The radius is given in the question

Radius $= 8m$

Use the formula $\pi r^2$ to calculate the area of the circle.

\begin{aligned} &\pi r^2\\\\ &= \pi \times r\times r\\\\ &= \pi \times8\times 8\\\\ &= 64\pi \end{aligned}

Give your answer clearly with the correct units.

Remember the question asks you to give your answer to ‘in terms of $\pi$ .

64\pi\; m^2

Example 4: calculating the area of the circle given the diameter

A circle has a diameter of $420km.$ , calculate its area.
Give your answer in terms of $\pi$

Find the radius of the circle.

In this question the question gives you the diameter. You need the radius to find the area of the circle.

Diameter $= 420km$

Radius $= 420km \div 2$

Radius $= 210km$

Use the formula $\pi r^2$ to calculate the area of the circle.

\begin{aligned} &\pi r^2\\\\ &= \pi \times r\times r\\\\ &= \pi \times210\times 210\\\\ &= 44100\pi \end{aligned}

Give your answer clearly with the correct units.

You leave the answer in the form $44100 \pi$

44100\pi\; km^2

Example 5: calculating the area of the circle given the circumference of a circle

A circle has a circumference of $21cm$ , calculate its area.
Give your answer to $2dp$ .

Find the radius of the circle.

The question gives you the circumference of the circle. But you need the radius

You know that the circumference of a circle is equal to $2\pi r$

This means you can find the radius of the circle from the circumference, see below:

Circumference $= 2\pi r$

Circumference $= 21$

$21 = 2\pi r$

Divide both sides by $2\pi$

$\frac{21}{2\pi}= r$

Notice how we leave our answer in terms of $\pi$ at this stage. This is so you do not cause a rounding error later on in the question.

Use the formula $\pi r^2$ to calculate the area of the circle.

\begin{aligned} &\pi r^2\\\\ &= \pi \times r\times r\\\\ &= \pi \times\frac{21}{2\pi}\times \frac{21}{2\pi}\\\\ &=35.09366.. \end{aligned}

Give your answer clearly with the correct units.

Remember the question asks you to round your answer to ‘2 decimal place’

35.09cm^2

Example 6: calculating the area of a semi-circle given the diameter

A semicircle has a diameter of $20m.$ , calculate its area.

Give your answer in terms of $\pi$

Find the radius of the circle.

In this question the question gives you the diameter. You need the radius to find the area of the circle.

Remember the diameter of the circle is twice the radius.

Diameter $= 20m$

Radius $= 20m \div 2$

Radius $= 10m$

Use the formula $\pi r^2$ to calculate the area of the circle.

\begin{aligned} &\pi r^2\\\\ &= \pi \times r\times r\\\\ &= \pi \times 10\times 10\\\\ &= 100\pi \end{aligned}

This represents the area of a whole circle with a diameter of 20m.
A semi circle has half the area of a full circle so you need to divide your answer by two. Remember to keep it in terms of $\pi$ .

$\begin{aligned} &100\pi \div2 \\\\ &50\pi \end{aligned}$

Give your answer clearly with the correct units.

50 \pi\; m^2

Common misconceptions

Radius

You must have the radius to find the area of a circle by using the formula. If a question does not give the radius directly then it must be calculated.

Correct units

When working with area you must always give the correct units squared
E.g.
$cm^2 , m^2, km^2$ etc.

Rounding

It is important to only round at the end of the question and ensure you are round to what the question specifies.
E.g. to 2 decimal places

In terms of $\pi$

Sometimes the question may ask you to give the answer in terms of $\pi$ ’. This means you do not give the numerical answer that is produced when you multiply it by $\pi$

E.g.

6 x $\pi$ = 6 $\pi$ (this is an answer in terms of pi)

6 x $\pi = 18.8495592…$ (this answer is not in terms of pi)

Misuse of calculator

Ensure you know how to correctly use the $\pi$ button on your calculator.

Practice area of a circle questions

6cm

3cm

12cm

6\pi cm

The diameter of the circle is twice the size of the radius. Therefore to find the radius you can divide the diameter by $2.$

6cm \div 2 = 3cm

31.4cm

20m

10\pi cm

24.5

$10 \pi$ means $10$ lots of $\pi$

\pi cm^2

\pi cm

3.1cm

3.1 cm^2

Area of a circle $= \pi r^2$

$\pi \times 1 \times 1$ is equal to $3.1415\dots$

This answer is correctly rounded to $1$ decimal place and has the correct units.

\pi cm^2

\pi cm

3.1cm

3.1 cm^2

Area of a circle $= \pi r^2$

$\pi \times 1 \times 1$ is equal to $\pi$

This answer is correctly given in terms of $\pi$ and has the correct units.

4\pi cm^2

\pi cm^2

3.1cm

3.1 cm^2

You must first divide the diameter by $2$ to find the radius, $2cm$ divided by $2$ is equal to $1cm.$

Therefore the radius is $1cm$

Area of a circle $= \pi r^2$

$\pi \times 1 \times 1$ is equal to $\pi$

This answer is correctly given in terms of $\pi$ and has the correct units.

31416 cm^2

31415 cm^2

31415.9 cm^2

10000\pi cm^2

Area of a circle $= \pi r^2$

$\pi \times 100 \times 100$ is equal to $31415.92654\dots$

Which is $31416 cm^2$ rounded to the nearest whole number.

Area of a circle GCSE questions

1. The radius of a circle is $3.5 cm$ .
Work out the area of the circle.
Give your answer correct to $3$ significant figures.

(3 marks)

Show answer

$\pi \times3.5\times 3.5$ or $38.4845\dots$ seen

(1)

38.5

(1)

cm^2

(1)

2. The radius of a circle is $17.2 m$ .
Work out the area of the circle.
Give your answer correct to $2$ decimal places.

(3 marks)

Show answer

$\pi \times17.2\times 17.2$ or $929.408\dots$ seen

(1)

929.41

(1)

m^2

(1)

3. The diameter of a circle is $20mm$ .
Work out the area of the circle.
Give your answer in terms of $\pi$ .

(3 marks)

Show answer

\pi \times10\times 10

(1)

100\pi

(1)

mm^2

(1)

4. The diameter of a circle is $15cm$ .
Work out the area of the circle.
Give your answer to 1 decimal place.

(3 marks)

Show answer

\pi \times7.5\times 7.5

(1)

$176.7$ (1.d.p)

(1)

cm^2

(1)

5. The circumference of a circle is $72cm$ .
Work out the area of the circle.
Give your answer correct to the nearest integer.

(4 marks)

Show answer

$\frac{72}{2\pi}= r$ or $\frac{36}{\pi}= r$ seen

(1)

\pi \times\frac{72}{2\pi}\times \frac{72}{2\pi}

(1)

$412.52961\dots$ seen

(1)

413

(1)

6. A tile is in the shape of a semicircle.
The perimeter of a semi circle is $12.85cm$ and the length of the arc is $7.85cm$ .
Work out the total area of the tile.
Give your answer correct to the nearest integer.

Area of a circle GCSE question 6 1

(4 marks)

Show answer

Length of diameter $= 5cm$

(1)

\pi \times 2.5\times 2.5

$6.25\pi$ or $19.634\dots$ seen

(1)

$“19.634\dots” \div 2$ or $9.817\dots$ seen

(1)

10

(1)

7. The area of a circle is $64\pi cm^2$ .
Calculate the radius of the circle.

(3 marks)

Show answer

64\pi = \pi r^2

(1)

64 = r^2

(1)

r=8

(1)

Only positive value should be given

Learning checklist

You have now learned how to:

Identify and apply circle definitions and properties, including: centre, radius, chord, diameter, circumference
Know the formulae for area of a circle
Give answers in terms of $\pi$
Calculate area of 2D shapes including circles and semi-circles

The next lessons are

Circumference of a circle
Arc lengths
Area of a sector
Perimeter of a sector
Circle graph
Equation of a circle
Circle theorems
Surface area and volume of spheres

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction

What is the area of a circle?

What is pi?

How to calculate the area of a circle

Area of a circle worksheet

Area of a circle examples

↓

Example 1: calculating the area of the circle given the radius Example 2: calculating the area of the circle given the diameter Example 3: calculating the area of the circle, given the radius, answer in terms of 𝝅 Example 4: calculating the area of the circle given the diameter Example 5: calculating the area of the circle given the circumference of a circle Example 6: calculating the area of a semi-circle given the diameter

Common misconceptions

Practice area of a circle questions

Area of a circle GCSE questions

Learning checklist

Next lessons

Still stuck?