Circle graph

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

Circles, sectors and arcs Substitution Coordinates maths Gradient of a line Parallel and perpendicular Equation of a line

This topic is relevant for:

GCSE Maths Algebra Types Of Graphs

Circle Graph

Here we will learn about circle graphs, including how to recognise them and how to sketch them. We will also look at solving coordinate geometry questions involving circle graphs.

There are also circle graphs worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a circle graph?

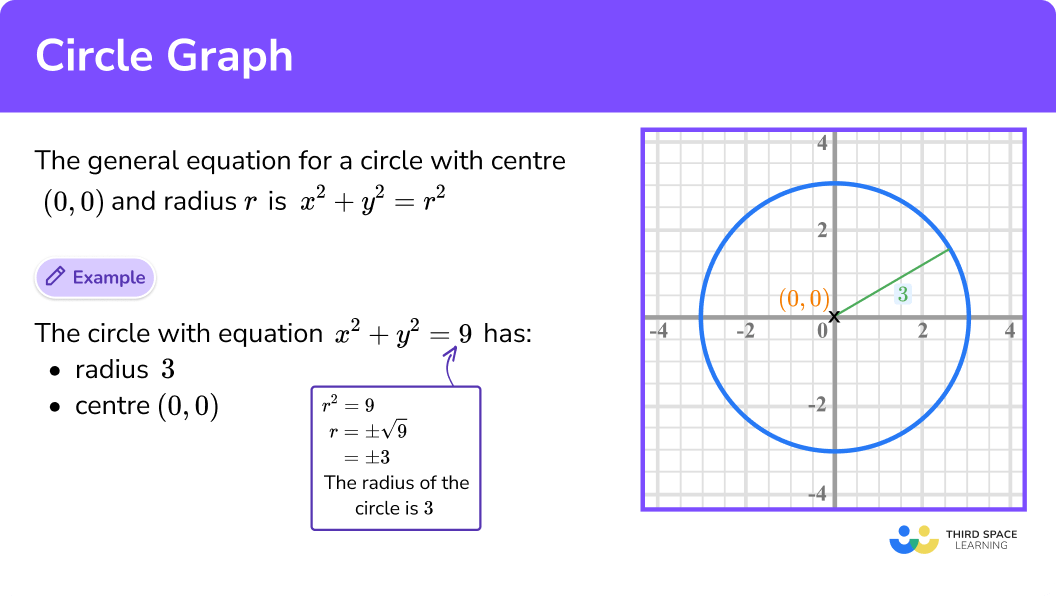
A circle graph is the graph of an equation which forms a circle.

To do this we have a circle with radius r and centre (0, 0).
Using Pythagoras’ Theorem it gives the general equation:

\[x^2+y^2=r^2\]

E.g.
This circle has a radius of 3 so has the equation:

\[x^2+y^2=3^2\]

Which simplifies to:

\[x^2+y^2=9\]

What is a circle graph?

How to recognise the equation of a circle

In order to recognise the equation of a circle:

Identify an $x^2$ term and a $y^2$ term
Check the radius and use $r^2$
Identify your final answer

Circle graph worksheet

Get your free circle graph worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Circle graph worksheet

Get your free circle graph worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Circle graph is part of our series of lessons to support revision on types of graphs. You may find it helpful to start with the main types of graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Circle graph examples

Example 1: recognise the equation of a circle

Identify the correct equation for the graph:

\[ y=x^2+6 \quad \quad \quad y=x^2+12 \quad \quad \quad x^2+y^2=36 \quad \quad \quad x^2+y^2=12\]

Identify an $x^2$ term and a $y^2$ term

The equation $y=x^2+6$ only has an $x^2$ term and is a quadratic function.

The equation $y=x^2+12$ only has an $x^2$ term and is also a quadratic function.

Both the equation $x^2+y^2=36$ and the equation $x^2+y^2=12$ have an $x^2$ term and a $y^2$ term.

2Check the radius and use $r^2$

The radius of the circle is 6, so

\[r^2=6^2=36\]

3Identify your final answer

The correct equation for the graph is:

\[x^2+y^2=36\]

Example 2: recognise the equation of a circle

Identify the correct equation for the graph:

\[x^2+y^2=20 \quad \quad \quad y=x^3+10 \quad \quad \quad y=x^2+20 \quad \quad \quad x^2+y^2=100\]

Identify an $x^2$ term and a $y^2$ term

The equation $y=x^2+20$ only has an $x^2$ term and is a quadratic function.

The equation $y=x^3+10$ only has an $x^3$ term and is a cubic function.

Both the equation $x^2+y^2=20$ and the equation $x^2+y^2=100$ have an $x^2$ term and a $y^2$ term.

Check the radius and use $r^2$

The radius of the circle is 10, so

\[r^2=10^2=100\]

Identify your final answer

The correct equation for the graph is:

\[x^2+y^2=100\]

How to sketch a circle graph

In order to sketch a circle graph:

Check the radius
Draw a circle with centre (0, 0)
Label where the circle crosses the axes

Explain how to sketch a circle graph

Sketching a circle graph examples

Example 3: sketching a circle graph

Sketch $x^2+y^2=64$

Check the radius

The equation of a circle graph with centre (0, 0) is of the form:

\[x^2+y^2=r^2\]

\[\begin{align*} r^2 &= 64 \\\\ r &= \sqrt{64}\\\\ r &=8 \end{align*} \]

Draw a circle with centre (0, 0)

Label where the circle crosses the axes

\[x^2+y^2=64\]

Example 4: sketching a circle graph

Sketch $x^2+y^2=144$

Check the radius

The equation of a circle graph with centre (0, 0) is of the form:

\[x^2+y^2=r^2\]

\[\begin{align*} r^2 &= 144 \\\\ r &= \sqrt{144}\\\\ r &=12 \end{align*} \]

Draw a circle with centre (0, 0)

Label where the circle crosses the axes

\[x^2+y^2=144\]

How to find the equation of a tangent to a circle

In order to find the equation of a tangent to a circle:

Find the gradient of the radius from the given point to the centre
Find the gradient of the perpendicular
Find the equation of the lines using the gradient and the given point
Write the equation of the tangent

Finding the equation of a tangent to a circle examples

Example 5: finding the equation of a tangent to a circle

Find the equation of the tangent to the circle $x^2+y^2=90$ at the point $(9,3)$

Find the gradient of the radius from the given point to the centre

The gradient of the radius is:

\[\frac{Change\hspace{2mm}in\hspace{2mm}y}{Change\hspace{2mm}in\hspace{2mm}x}=\frac{3}{9}=\frac{1}{3} \]

Find the gradient of the perpendicular

The radius and the tangent meet at right angles; this is a circle theorem.
Therefore the radius and the tangent are perpendicular.

The product of perpendicular gradients is −1.

\[m_1 \times m_2=-1\]

So the gradient of the tangent is:

−3

Find the equation of the lines using the gradient and the given point

The equation of a straight line is of the form:

\[y=mx+c\]

We can substitute the original point for the x and y values.
The gradient of the tangent is the value of m.
We can then work out c.

\[\begin{align*} y &= mx+c \\\\ 3 &= -3 \times 9 +c\\\\ 3 &= -27 +c\\\\ 30 &= c \end{align*} \]

Write the equation of the tangent

\[y=-3x+30\]

Example 6: finding the equation of a tangent to a circle

Find the equation of the tangent to the circle $x^2+y^2=13$ at the point $(-3,2)$

Find the gradient of the radius from the given point to the centre

The gradient of the radius is:

\[\frac{Change\hspace{2mm}in\hspace{2mm}y}{Change\hspace{2mm}in\hspace{2mm}x}=\frac{2}{-3}=-\frac{2}{3} \]

Find the gradient of the perpendicular

The radius and the tangent meet at right angles; this is a circle theorem.
Therefore the radius and the tangent are perpendicular.

The product of perpendicular gradients is −1.

\[m_1 \times m_2=-1\]

So the gradient of the tangent is:

\[\frac{3}{2}\]

Find the equation of the lines using the gradient and the given point

The equation of a straight line is of the form:

\[y=mx+c\]

We can substitute the original point for the x and y values.
The gradient of the tangent is the value of m.
We can then work out c.

\[\begin{align*} y &= mx+c \\\\ 2 &= \frac{3}{2} \times -3 +c\\\\ 2 &= \frac{-9}{2} +c\\\\ \frac{13}{2} &= c \end{align*} \]

Write the equation of the tangent

\[y=\frac{3}{2}x+\frac{13}{2}\]

Common misconceptions

Make sure that you use $r^2$

The equation of the circle requires the radius NOT the diameter.

Remember the radius is half the diameter.

The radius is always a positive number

Since the radius is a length it is always positive.

E.g.

The radius of this circle is $12$ and $r^2=144$ . The equation of this circle is $x^2+y^2=144$

Practice circle graph questions

x^2+y^2=125

x^2+y^2=10

x^2+y^2=5

x^2+y^2=25

The equation of a circle graph with centre $(0,0)$ is of the form:

x^2+y^2=r^2

The radius of the circle is $5$ , so

r^2=5^2=25

x^2+y^2=49

x^2+y^2=-49

x^2+y^2=14

x^2+y^2=-14

The equation of a circle graph with centre $(0,0)$ is of the form:

x^2+y^2=r^2

The radius of the circle is $7$ , so

r^2=7^2=49

Circle Graph Practice question 3 (2) 1

Circle Graph Practice Question 3 1

Circle Graph Practice question 3(3) 1

Circle Graph Practice question 3 (4) 1

The equation of a circle graph with the centre of the circle $(0,0)$ is of the form:

x^2+y^2=r^2

\begin{aligned} r^2 &= 16 \\ r &= \sqrt{16}\\ r &=4 \end{aligned}

So we draw a circle with centre $(0,0)$ radius of the circle is $4.$

Circle Graph Practice question 4 (3) 1

Circle Graph Practice question 4 (2) 1

Circle Graph Practice question 4 1

Circle Graph Practice question 4 (4) 1

The equation of a circle graph with centre $(0,0)$ is of the form:

x^2+y^2=r^2

\begin{aligned} r^2 &= 81 \\ r &= \sqrt{81}\\ r &=9 \end{aligned}

So we draw a circle with centre $(0,0)$ radius of the circle is $4.$

y=-\frac{1}{2}x+20

y=2x+20

y=-2x+32

y=-2x+20

The gradient of the radius is:

\frac{change\hspace{1mm}in\hspace{1mm}y}{change\hspace{1mm}in\hspace{1mm}x}=\frac{4}{8}=\frac{1}{2}

The gradient of the tangent will be: $-2$

\begin{aligned} y &= mx+c \\ 4 &= -2 \times 8 +c\\ 4 &= -16 +c\\ 20 &= c \end{aligned}

So the equation would be:

y=-2x+20

y=\frac{1}{2}x+5

y=2x+5

y=2x+4

y=-\frac{1}{2}x+4

The gradient of the radius is:

\frac{change\hspace{1mm}in\hspace{1mm}y}{change\hspace{1mm}in\hspace{1mm}x}=\frac{4}{-2}=-2

The gradient of the tangent will be: $\frac{1}{2}$

\begin{aligned} y &= mx+c \\ 4 &= \frac{1}{2} \times -2 +c\\ 4 &= -1 +c\\ 5 &= c \end{aligned}

So the equation would be:

y=\frac{1}{2}x+5

Circle graph GCSE questions

1. Identify the equation of this graph:

Circle graph GCSE question 1 1

x^2+y^2=20 \quad \quad x^2+y^2=10 \quad \quad x^2+y^2=100 \quad \quad x^2+y^2=5

(1 Mark)

Show answer

The equation of a circle graph with centre $(0,0)$ is of the form:

x^2+y^2=r^2

The radius of the circle is $10$ , so

r^2=10^2=100

The correct equation is:

x^2+y^2=100

(1)

2. A point $P (2,4)$ lies on the circle with equation:

x^2+y^2=20

Find the equation of the tangent to the circle at the point $P.$

(3 Marks)

Show answer

Gradient of OP, the radius is $2$

\frac{change\hspace{1mm}in \hspace{1mm}y}{change\hspace{1mm}in\hspace{1mm}x}=\frac{4}{2}=2

(1)

The gradient of the tangent is $-\frac{1}{2}$

(1)

\begin{aligned} y &= mx+c \\\\ 4 &= -\frac{1}{2} \times 2 +c\\\\ 4 &= -1 +c\\\\ 5 &= c \end{aligned}

The equation of the tangent is:

y=-\frac{1}{2}x+5

(1)

3. (a) On the grid, draw the graph of:

x^2+y^2=16

Circle graph GCSE question 3a 1

(b) Hence find estimates for the solutions of simultaneous equations:

x^2+y^2=16

x+y=3

(3 Marks)

Show answer

(a)

Circle graph GCSE question 3a (2) 1

for a circle with centre $(0.0)$

(1)

for the correct circle with radius $4$

(1)

(b)

Circle graph GCSE question 3b 1

$x=3.9$ and $y= -0.9$

$x= -3.9$ and $y=0.9$

for drawing the line graph $x+y=3$

(1)

for one of the correct pair of $x$ and $y$ solutions OR both $x$ -values OR both $y$ -values

(1)

for both pairs of correct solutions

(1)

Learning checklist

You have now learned how to:

recognise the equation of a circle with centre at the origin

use the equation of a circle with centre at the origin

find the equation of a tangent to a circle at a given point

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.