Parallel and perpendicular lines

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Rearranging formulae Solving equations Reciprocal maths Plotting graphs

This topic is relevant for:

GCSE Maths Algebra Types Of Graphs Straight Line Graphs

Parallel And Perpendicular Lines

Here we will learn about parallel and perpendicular lines including how to show when two lines are parallel or perpendicular, how to calculate the gradient of parallel and perpendicular lines and use this knowledge to calculate the gradient of tangents to circles.

There are also parallel and perpendicular worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are parallel and perpendicular lines?

Parallel lines are straight lines with a constant distance between them.
Perpendicular lines intersect one another at a 90 degree angle (a right angle)

E.g.
A table has 4 legs. Each leg is parallel to the other legs, but perpendicular to the table top that they are attached to:

Straight line graphs can be parallel, perpendicular or have 1 point of intersection. It is not possible for 1 straight line to intersect another line at two coordinates or be parallel and perpendicular at the same time. We therefore need to understand each property so that we can start to visualise when lines are parallel or perpendicular.

What are parallel and perpendicular lines?

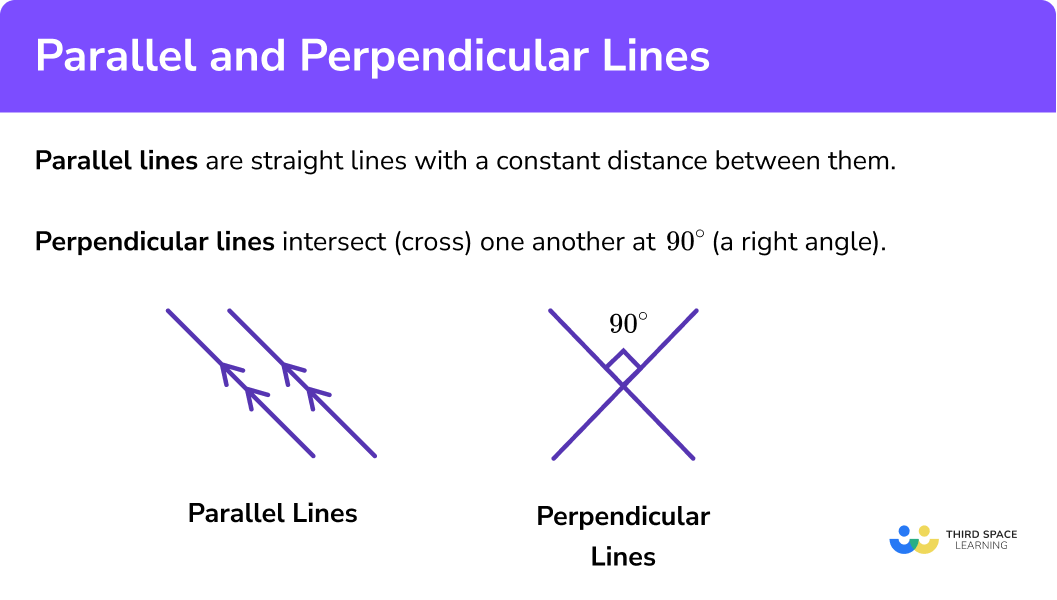
Parallel lines

Two (or more) straight lines are parallel when they share the same gradient.

E.g.
Let’s look at the three lines y = 2x + 1, y = 2x + 5 and y = 2x − 3:

Each straight line has the same gradient (here, m = 2) and the distance between any two lines remains constant in both directions. This means that all 3 lines are parallel.

We can therefore state that the equation of a line parallel to a line with the gradient 2 can be written in the form y = 2x + c, for any value of c that represents where the graph intercepts the y-axis.

Top Tip: All vertical lines are parallel to the line x = 0 and all horizontal lines are parallel to the line y = 0.

See also: Gradient of a line

What are parallel lines?

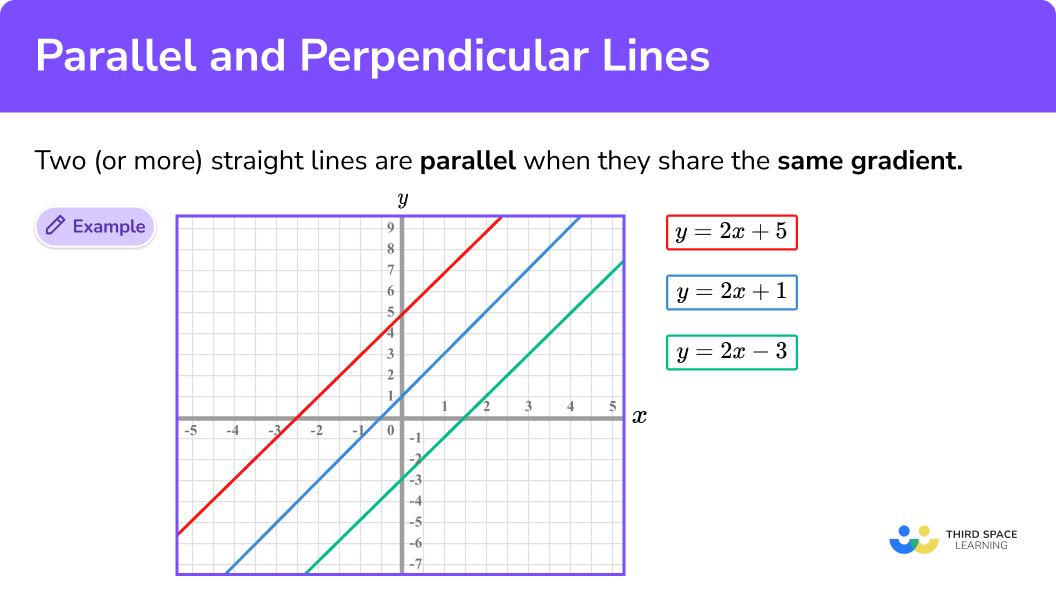
Equations of parallel lines

Parallel lines can be recognised by their equations by checking if their gradients are the same. This may require some rearranging.

E.g.

Show that $y=-2x+4$ and $4x+2y=9$ are parallel.

The gradient of the first line is $-2$ . We need to rearrange the second equation so that it is in the form $y=mx+c$ so we can find the gradient.

4x+2y=9

2y=-4x+9

y=-2x+4.5

The gradient of the second line is also -2. The gradients of the two lines are the same, so the lines are parallel.

Perpendicular lines

Perpendicular lines have gradients that multiply to give −1.
In other words, the gradients of two lines that are perpendicular to each other are the negative reciprocals of each other.

E.g.
To see why let’s look at the line y = x:

The gradient of the line y = x is m = 1 as for each unit square we move right along the x-axis, we move 1 unit square up the y-axis.

Let’s now construct a line that is perpendicular to the line y = x; we can do this by finding the perpendicular bisector for the line between the points $(-3, -3)$ and $(3, 3)$ :

The equation of a straight line that is perpendicular to the line y = x is the line y = −x.

We can see that the gradient of each line has a different sign (one has a positive gradient whilst the other has a negative gradient).
To find out what is going on here let’s look at a second example.

E.g.
Take the line y = 2x + 3.

Let’s construct a perpendicular to the line y = 2x + 3 at the point (0,3)

Here the equation of the line that is perpendicular to $y = 2x + 3$ at the point $(0, 3)$ is $y=−\frac{1}{2}x+3$

We can still state that the gradients change from being positive to negative but we now have the gradient of $-\frac{1}{2}$ which is the negative reciprocal of $2$ .

Let us look at the previous two examples together in the table below:

Gradient of line 1	Gradient of line 2	Product of both gradients
1	-1	1 × (-1) = -1
2	-½	2 × -½ = -1

Here we can see that the product of the gradients of each line is equal to −1.

We can therefore state that for any two perpendicular lines y = mx + c and y = nx + c,

mn = −1.

If we divide both sides of the formula by m, we get the formula for the gradient of the perpendicular line n to be: $n=\frac{−1}{m}$ .

The value of n is called the negative reciprocal of m as we divide −1 by m.

What are perpendicular lines?

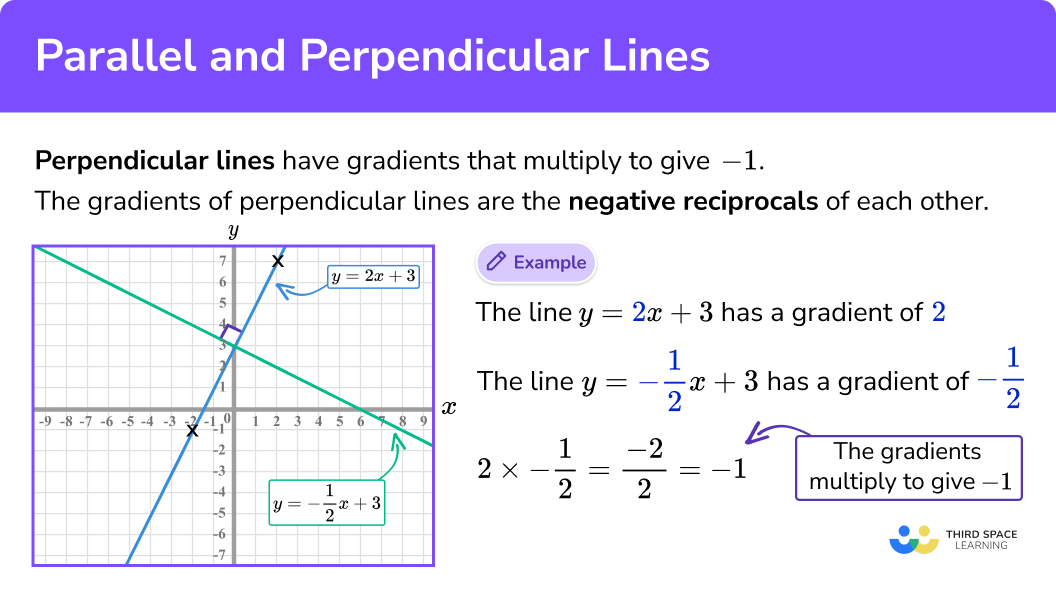
Gradients of parallel and and perpendicular lines

The gradients of parallel lines are the same.

The gradients of perpendicular lines multiply together to make $-1.$

Here is a brief summary.

For any two lines to be parallel, the gradient is the same for each line.

E.g.
$y = 5x + 3$ and $y = 5x - 9$ are parallel as the gradient for each line is $5$ .

For any two lines to be perpendicular, the product of their gradients must equal −1.

E.g.
$y=4x+7$ and $y=-\frac{1}{4}x+9$ are perpendicular as $4\times-\frac{1}{4}=-1$

How to find the equation of a parallel line

In order to find the equation of a parallel line:

State/calculate the gradient of the original straight line.
Substitute the value for m into the equation of a new straight line.
State/calculate the value of the $\textbf{y}$ -intercept.

How to find the equation of a parallel line

Parallel and perpendicular lines worksheet

Get your free parallel and perpendicular lines worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Parallel and perpendicular lines worksheet

Get your free parallel and perpendicular lines worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on straight line graphs

Parallel and perpendicular lines is part of our series of lessons to support revision on straight line graphs. You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Parallel lines examples

Example 1: write the equation of a parallel line (algebraically)

The equation of a line $A$ is given as $5y = x - 10$ .
Write the equation of a line that is parallel to $A$ .

State/calculate the gradient of the original straight line.

As $5y=x-10$ .

Here, the gradient of the line is $\frac{1}{5}$

2Substitute the value for m into the equation of a new straight line.

Substituting $m=\frac{1}{5}$ into a new equation, we get $y=\frac{1}{5}x+c$

3State/calculate the value of the y-intercept.

Here we are asked to state a parallel line so any value of c, except for the value stated in the original equation (−2), would satisfy this question.

An example of an equation of the line parallel to line A is $y=\frac{1}{5}x+3$

Example 2: write the equation of a parallel line (graphically)

The line B is drawn on a set of axes. Write the equation of a line that is parallel to B.

State/calculate the gradient of the original straight line.

Here,

\[\\m=\frac{-3}{3}=-1\\\]

Substitute the value for m into the equation of a new straight line.

We now have y = −x + c

State/calculate the value of the y-intercept.

Here we are asked to state a parallel line so any value of c, except for the value stated in the original equation (3), would satisfy this question.

A possible solution would be y = −x − 4.

Example 3: given 1 coordinate and the gradient

Two lines, D and E are written in the form y = mx + c.
The gradient of the line D is equal to 0.4 and intersects the y-axis at the point (0,5).
The line E is parallel to D and goes through the point (10,12).
Work out the equation of line E.

State/calculate the gradient of the original straight line.

We know from the question that the gradient of line D is 0.4.

Substitute the value for m into the equation of a new straight line.

We now have y = 0.4x + c.

State/calculate the value of the y-intercept.

We need to calculate the value of c as it is stated that the line E goes through the point (10,12). We therefore substitute x = 10 and y = 12 into the equation to find the value of c.

\begin{aligned} \\12&=0.4\times{10}+c\\ \\12&=4+c\\ \\c&=8 \end{aligned}

The equation of line E is y = 0.4x + 8

How to calculate the equation of perpendicular lines

In order to find the equation of a perpendicular line:

State/calculate the gradient of the original straight line.
Calculate the negative reciprocal of the gradient.
Substitute the negative reciprocal into the equation of a new straight line.
State/calculate the value of the $\textbf{y}$ -intercept.

How to calculate the equation of perpendicular lines

Perpendicular lines examples

Example 1: write the equation of a perpendicular line (algebraically)

The equation of a line A is given as 2y + 7 = 8x. Write the equation of a line that is perpendicular to A.

State/calculate the gradient of the original straight line.

First we need to rearrange the equation to make y the subject. This in turn will give us the value for the gradient m.

Now we can see that m = 4.

Calculate the negative reciprocal of the gradient.

The gradient of the line perpendicular to A is equal to

\[\\n=\frac{-1}{m}=\frac{-1}{4}\\\]

Substitute the negative reciprocal into the equation of a new straight line.

We now have the equation $y=-\frac{1}{4}x+c$ for the line perpendicular to A.

State/calculate the value of the y-intercept.

Here, we are asked to state a perpendicular line so any value of c would satisfy this question.

An example of an equation of the line perpendicular to line A is $y=-\frac{1}{4}x+1$

Example 2: write the equation of a perpendicular line (graphically)

The line B is drawn on a set of axes. Write the equation of a line that is perpendicular to B at the point (1,4).

State/calculate the gradient of the original straight line.

Here,

\[\\m=\frac{-8}{4}=-2\\\]

Calculate the negative reciprocal of the gradient.

The gradient of the line perpendicular to B is equal to

\[\\n=\frac{-1}{m}=\frac{-1}{-2}=\frac{1}{2}\\\]

Substitute the negative reciprocal into the equation of a new straight line.

We now have the equation $y=\frac{1}{2}x+c$ for the line perpendicular to B.

State/calculate the value of the y-intercept.

Here we have to substitute the coordinate (1,4) into the new equation for our straight line to find the value of c.

\[\\4=\frac{1}{2}\times{1}+c\\\]

\[\\4=\frac{1}{2}+c\\\]

\[\\c=3\frac{1}{2}\\\]

The equation of the line that is perpendicular to the line B is $y=\frac{1}{2}x+3\frac{1}{2}$ or $2y=x+7$ .

Example 3: given 1 coordinate and the gradient

Two lines, D and E are written in the form y = mx + c.
The gradient of the line D is equal to $-\frac{2}{5}$ and intersects the y-axis at the origin. The line E is perpendicular to D. Work out the equation of line E.

State/calculate the gradient of the original straight line.

The gradient of line D is $-\frac{2}{5}$ as stated in the question.

Calculate the negative reciprocal of the gradient.

Here, we have

\[\\n=-1\div{-\frac{2}{5}}\\ \\n=-1\times{-\frac{5}{2}}\\ \\n=\frac{5}{2}\\\]

Substitute the negative reciprocal into the equation of a new straight line.

Substituting $m=\frac{5}{2}$ into $y=mx+c$ we get $y=\frac{5}{2}x+c$

State/calculate the value of the y-intercept.

Here we have to substitute the coordinate (0,0) into the new equation for our straight line to find the value of c.

\[\\0=0\times{\frac{5}{2}}+c\\\]

\[c=0\]

The equation of line E is therefore $y=\frac{5}{2}x$

Common misconceptions

Using the y-intercept instead of the coefficient of x (parallel lines)

E.g.
Take example 1: “The equation of a line A is given as 5y = x − 10. Write the equation of a line that is parallel to A.”
After making y the subject so we have the equation $y=\frac{1}{5}x−2$ the value for the gradient could be incorrectly taken as –2. This will generate a new equation that looks like y = mx − 2 which is incorrect as it is the coefficient of x that remains the same, and the y-intercept changes.

Not/incorrectly rearranging to the form y = mx + c

The gradient is the coefficient of x, labelled as m.
If the equation of a straight line is not written with y as the subject, the gradient may not be correct so it is important to be confident with rearranging equations.
E.g.
Take example 1 again: “The equation of a line A is given as 5y = x − 10. Write the equation of a line that is parallel to A.”
Here, the value of the gradient could be incorrectly stated as 1 as the coefficient of x is 1. This is wrong because the equation is not in the form y = mx + c.

The reciprocal vs the negative reciprocal

A common mistake is to state the gradient of the perpendicular to a line to be the reciprocal of the original gradient, and not the negative reciprocal.
If the negative reciprocal was not used his would mean that both lines would have a positive gradient, or they would both have a negative gradient. This would mean that although the two lines may intersect they will not intersect at 90°.

Practice parallel and perpendicular lines questions

y=7+4x

y=2x+5

y=-\frac{1}{4}x+3

y=-4x+3

Any equation of the form $y=4x+c$ for any value of $c$ .

4y-10=3x

y=3x+5

2y=-4x+5

y=1.5x+4

Both have the gradient of $1.5$ (or $m=\frac{3}{2}$ )

m=0.4

m=4

m=2.5

m=-0.4

The product of the two gradients must equal $-1$ .
Here, $-1\div-0.4 = 1\div0.4 = 2.5$

m=\frac{7}{10}

m=-1

m=-\frac{10}{7}

m=1\frac{3}{7}

The product of the two gradients must equal $-1$ .

Here, $\frac{-7}{10}\times\frac{10}{7}=\frac{-70}{70}=-1$

y=2x+8

y=2x+2

y=2x+8

y=-\frac{1}{2}x+2

The line must have a gradient of $2$ so $y=2x+c$ .
At the point ( $3,8$ ), $8=2\times3+c$ , so $c=2$

Hence, $y=2x+2$

y=\frac{1}{3}x+6\

y=3x-19

y=-3x+1

y=3x+1

New gradient = $-1\div{-\frac{1}{3}}=-1\times{-3}=3$
$y=3x+c$ at the point ( $6,-1$ ) means $-1=(3\times6)+c$
$c=-19$

Parallel and perpendicular lines GCSE questions

1. Two straight lines A and B are shown below. Prove that the lines are parallel.

(3 marks)

Show answer

Gradient of line A = $\frac{2−1}{2−0}=\frac{1}{2}$

(1)

Gradient of line B = $\frac{0−−2}{4−0}=\frac{2}{4}=\frac{1}{2}$

(1)

Gradients are the same, therefore parallel

(1)

2. (a) Circle the equation of the line that is parallel to the y-axis.

x=3

x+y=0

y=-1

xy=4

(b) Use the straight line graph L below to write the equation of a parallel line passing through the coordinate ( $3,4$ )

(4 marks)

Show answer

a) $x = 3$

(1)

b) Gradient of line L is equal to − $1$

(1)

y = -x + c

(1)

$4 = -3 + c$ so $c = 7$ or $y = -x + 7$

(1)

3. (a) The line P has the equation $y=6−\frac{3}{5}x$ . Circle the gradient of a line that is perpendicular to P.

−\frac{5}{3}

\frac{3}{5}

\frac{5}{3}

5

(b) Point C ( $3,6$ ) lies on a circle, centre O. The tangent at C intersects the axes at points A and B. Show that the gradient of the tangent is $-\frac{1}{2}$

(3 marks)

Show answer

a) $\frac{5}{3}$

(1)

b) Gradient of OC= $\frac{6}{3}=2$

(1)

Gradient of perpendicular (tangent):
$AB=−1\div2$
$AB=−\frac{1}{2}$

(1)

4. Use the graph below to show that the two lines are parallel. Clearly state any conclusions.

(4 marks)

Show answer

(2)

$m=-\frac{6}{5}$ for both lines

(1)

The gradients are the same so the lines are parallel

(1)

Learning checklist

You have now learned how to:

Identify horizontal and vertical lines and pairs of perpendicular and parallel lines.

Use the form

y = mx + c

to identify parallel {and perpendicular} lines; find the equation of the line through 2 given points, or through 1 point with a given gradient.

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.