One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
This topic is relevant for:

How To Find The Midpoint
Here we will learn about how to find the midpoint, including finding the midpoint of a line segment using Cartesian coordinates, and finding a missing endpoint when the midpoint and other endpoint are given.
There are also midpoint of a line worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is the midpoint of a line?
The midpoint of a line segment is a point that lies exactly halfway between two points. It is the same distance from each endpoint of the straight line segment.
Sometimes we can work this out by inspection – this is easier with positive integer numbers.
For example, given the two points (2,2) and (8,6), the midpoint is exactly halfway between the two, and lies at (5, 4).
We can see that 5 is halfway between 2 and 8, and 4 is halfway between 2 and 6. Imagining a number line can help with this.
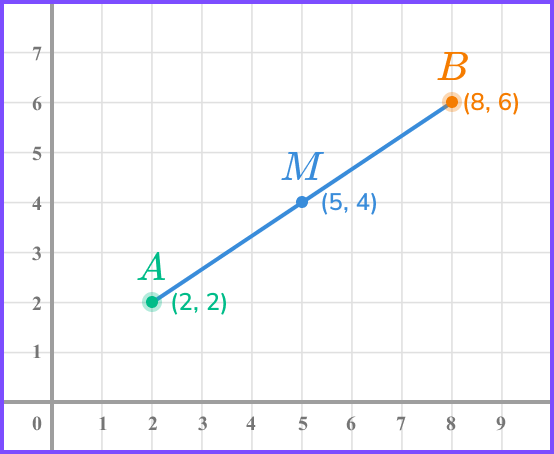
What is the midpoint of a line?
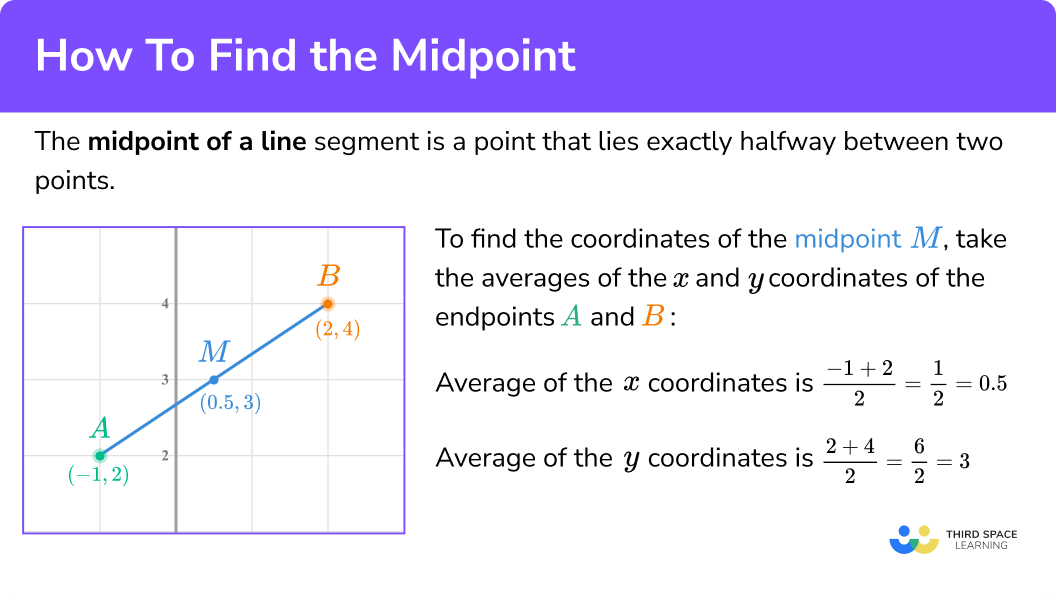
Midpoint of a line formula
If it is not easy to spot the midpoint, or the coordinates involve fractions or negative numbers, we can use the midpoint formula.
If the points \mathrm{A}\left(x_{1}, y_{1}\right) and \mathrm{B}\left(x_{2}, y_{2}\right) are the endpoints of a line segment, then the midpoint of the line segment joining the points A and B is \left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right).
This looks complicated when written algebraically, but we’re basically calculating the (mean) average of both the x values and the y values.
We sum the two x coordinates and divide by 2 to find the x coordinate of the midpoint, and we sum the two y coordinates and divide by 2 to find the y coordinate of the midpoint.
For example, given two points A \ (-1,2) and B \ (2,4), the midpoint (M) is exactly halfway between the two, and lies at (0.5, 3).
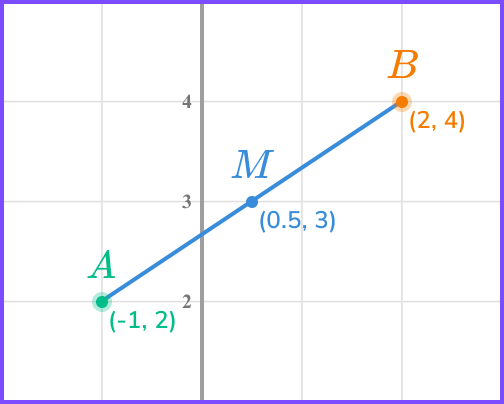
To calculate the midpoint,
The mean average of the x coordinates is \frac{-1+2}{2}=\frac{1}{2}=0.5.
The mean average of the y coordinates is \frac{2+4}{2}=\frac{6}{2}=3.
We can also apply the Pythagorean theorem to find the distance between two given points. To do this, we form a right-angled triangle with the line segment as the hypotenuse.
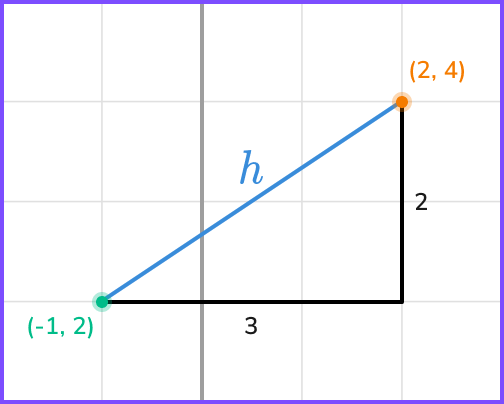
Pythagoras’ theorem tells us that h^{2}=2^{2}+3^{2}, and therefore the length of the hypotenuse is \sqrt{2^{2}+3^{2}}=\sqrt{13} .
Step-by-step guide: Pythagoras’ theorem
If you study coordinate geometry further at A Level, you may come across the general distance formula,
d=\sqrt{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)} where (x_{1},y_{1}) and (x_{2},y_{2}) are the coordinates of the two points and d is the distance between them.
How to find the midpoint of a line segment
In order to find the midpoint of the line segment joining the endpoints A and B:
- Find the average of the \textbf{x} coordinates of the two endpoints.
- Find the average of the \textbf{y} coordinates of the two endpoints.
- Write down the coordinates of the point.
Explain how to find the midpoint of a line segment

Straight line graph worksheet (includes how to find the midpoint)

Get your free worksheet of 20+ questions and answers. Includes reasoning and applied questions covering how to find the midpoint.
DOWNLOAD FREE
Straight line graph worksheet (includes how to find the midpoint)

Get your free worksheet of 20+ questions and answers. Includes reasoning and applied questions covering how to find the midpoint.
DOWNLOAD FREERelated lessons on straight line graphs
How to find the midpoint is part of our series of lessons to support revision on straight line graphs. You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
How to find the midpoint examples
Example 1: two positive integer endpoints
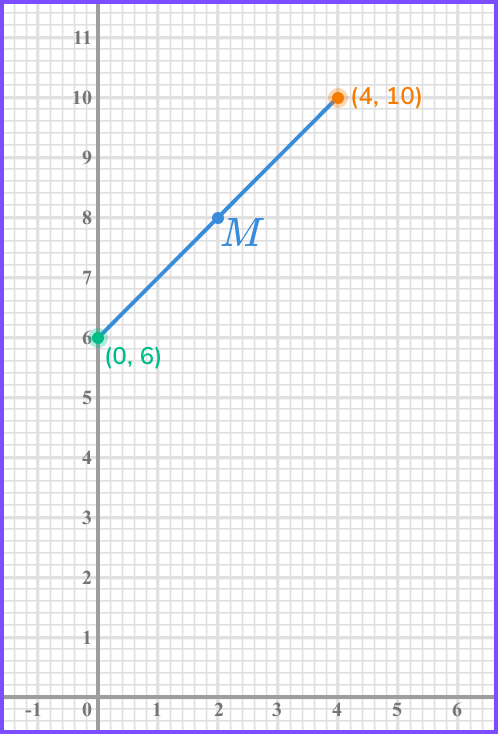
Find the midpoint of the line segment joining the points (0,6) and (4, 10).
- Find the average of the \textbf{x} coordinates of the two endpoints.
2Find the average of the \textbf{y} coordinates of the two endpoints.
\frac{6+10}{2}=\frac{16}{2}=83Write down the coordinates of the point.
(2, \ 8)In this case it is quite easy to see the midpoint by inspection, particularly if working on a graph.
Example 2: two positive integer endpoints with a fractional answer
Find the midpoint of the line segment joining the points (1,5) and (6, 0).
Find the average of the \textbf{x} coordinates of the two endpoints.
Find the average of the \textbf{y} coordinates of the two endpoints.
Write down the coordinates of the point.
It is generally OK to give coordinate pairs as short terminating decimals. Any longer or recurring decimals should be stated as fractions where possible, remembering to simplify your answer.
Example 3: coordinate pairs containing negative numbers
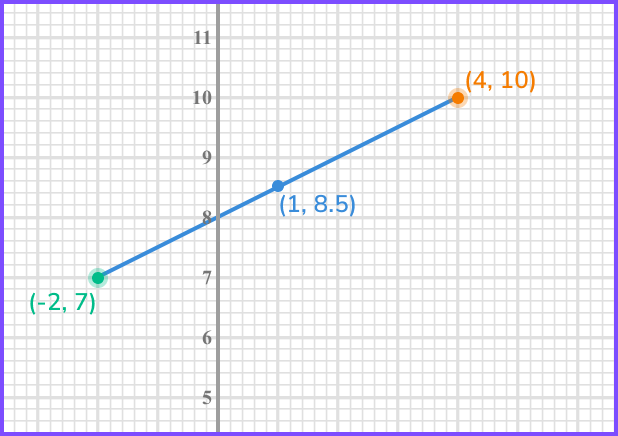
Find the midpoint of the line segment joining the points (-2,7) and (4, 10).
Find the average of the \textbf{x} coordinates of the two endpoints.
Find the average of the \textbf{y} coordinates of the two endpoints.
Write down the coordinates of the point.
Graphically,
Example 4: coordinates containing decimals
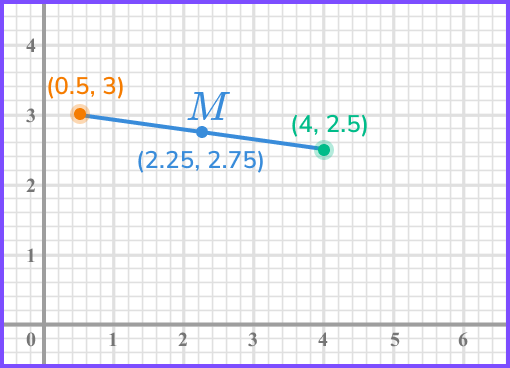
Find the midpoint of the line segment joining the points (0.5, 3) and (4, 2.5).
Find the average of the \textbf{x} coordinates of the two endpoints.
Find the average of the \textbf{y} coordinates of the two endpoints.
Write down the coordinates of the point.
Graphically,
Finding a missing endpoint
Sometimes you may be given one endpoint and the midpoint, and have to work out the other endpoint.
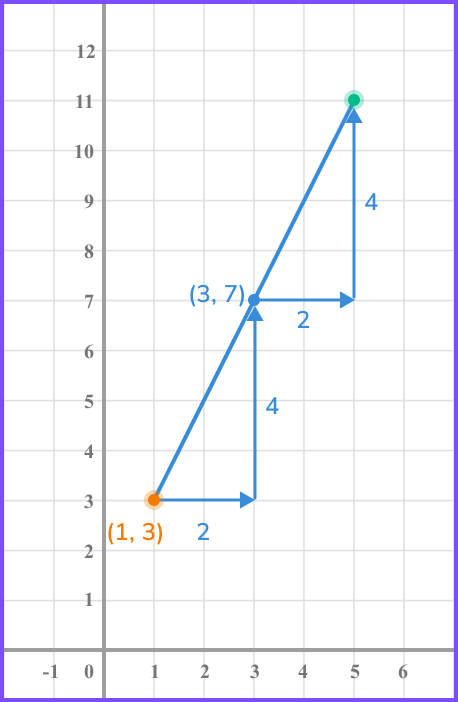
To get from the first endpoint (1,3) to the midpoint (3,7), we move 2 in the x -direction and 4 in the y -direction. So we just repeat this again from the midpoint to find the coordinate of the other endpoint, which in this case would be (5,11).
How to find a missing endpoint
In order to find a missing endpoint when given one endpoint and the midpoint:
- Work out how to get from the given endpoint to the midpoint.
- Repeat this to get from the midpoint to the missing endpoint.
- Write down the coordinates of the missing endpoint.
Explain how to find a missing endpoint

Example 5: finding a missing endpoint when given one endpoint and the midpoint
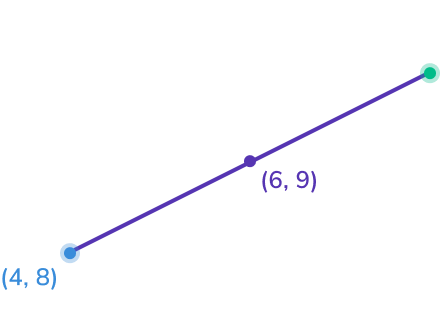
A line segment joins the points A and B, and has midpoint M.
A has coordinates (4, 8) and M has coordinates (6, 9).
Find the coordinates of point B.
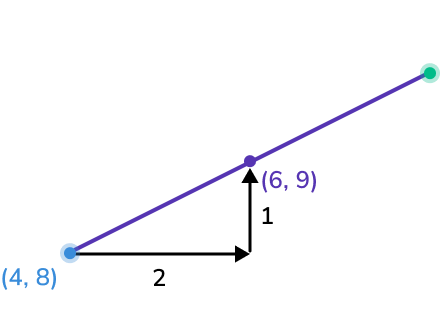
Work out how to get from the given endpoint to the midpoint.
To get from A to M, we add 2 to the x -coordinate of A and add 1 to the y -coordinate of A.
Repeat this to get from the midpoint to the missing endpoint.
To get from M to B, we add 2 to the x -coordinate of M and add 1 to the y -coordinate of M.
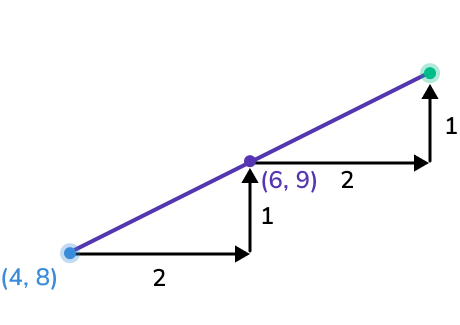
Write down the coordinate of the missing endpoint.
Therefore the coordinates of point B are (8,10).
Example 6: finding a missing endpoint with negative coordinates
A line segment joins the points A and B, and has midpoint M.
A has coordinates (-9, 4) and M has coordinates (-6, -1).
Find the coordinates of point B.
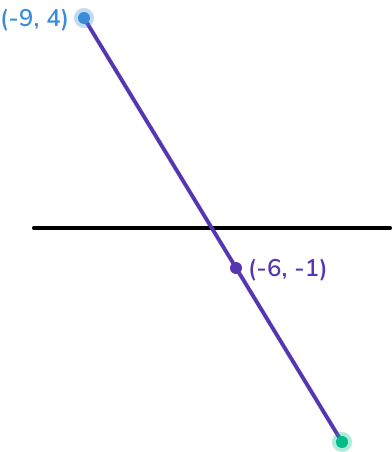
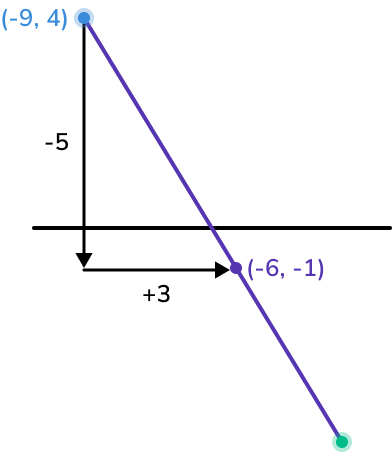
Work out how to get from the given endpoint to the midpoint.
To get from A to M, we add 3 to the x -coordinate of A and subtract 5 from the y -coordinate of A.
Repeat this to get from the midpoint to the missing endpoint.
To get from M to B, we add 3 to the x -coordinate of M and subtract 5 from the y -coordinate of M.
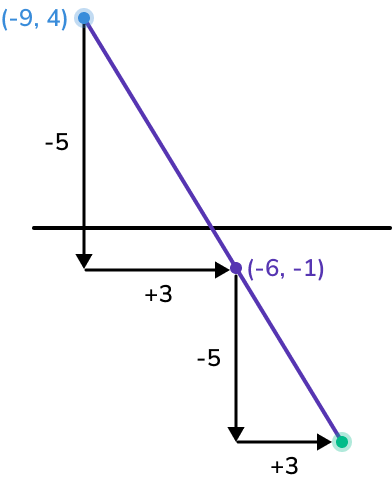
Write down the coordinate of the missing endpoint.
Therefore the coordinates of point B are (-3,-6).
Common misconceptions
- Finding the average of each point rather than the average of the \textbf{x} coordinates and average of the \textbf{y} coordinates
For example, for the points (2, 3) and (5, 7), make sure you don’t do \frac{2+3}{2} and \frac{5+7}{2}.
- Using the midpoint formula when given one endpoint and the midpoint
If one endpoint is (3, 4) and the midpoint is (6, 2), make sure you work out how you get from the endpoint to the midpoint and repeat this, rather than using the midpoint formula.
- Errors with negative number calculations
If you’re not sure about your answer, draw a diagram and count the steps.
Practice how to find the midpoint questions
1. Find the midpoint of the line segment joining the points (2, \ 8) and (6, \ 12).




The average of the x coordinates is \frac{2+6}{2}=\frac{8}{2}=4 and the average of the y coordinates is \frac{8+12}{2}=\frac{20}{2}=10.
2. Find the midpoint of the line segment joining the points (4, \ 10) and (7, \ 5).




The average of the x coordinates is \frac{4+7}{2}=\frac{11}{2}=5.5 and the average of the y coordinates is \frac{10+5}{2}=\frac{15}{2}=7.5.
3. Find the midpoint of the line segment joining the points (-2, \ 8) and (6, \ -2).




The average of the x coordinates is \frac{-2+6}{2}=\frac{4}{2}=2 and the average of the y coordinates is \frac{8+(-2)}{2}=\frac{6}{2}=3.
4. Find the midpoint of the line segment joining the points (3.5, \ 6) and (11, \ 8.5).




The average of the x coordinates is \frac{3.5+11}{2}=\frac{14.5}{2}=7.25 and the average of the y coordinates is \frac{6+8.5}{2}=\frac{14.5}{2}=7.5.
5. A line segment joins the points A and B, and has midpoint M.
A has coordinates (4, 2) and M has coordinates (9, 4) .
Find the coordinates of point B.




To get from A to M, add 5 to the x coordinate and add 2 to the y coordinate. Repeat this to get from M to B, so the coordinate of B is (14, \ 6).
6. A line segment joins the points A and B, and has midpoint M.
A has coordinates (3, 7) and M has coordinates (-1, 10).
Find the coordinates of point B.




To get from A to M, subtract 4 from the x coordinate and add 3 to the y coordinate. Repeat this to get from M to B, so the coordinate of B is (-5, \ 13).
How to find the midpoint GCSE questions
1. A line segment joins the points A and B, and has midpoint M.
A has coordinates (3, \ -12).
B has coordinates (-5, \ 10).
Work out the coordinates of M.
(2 marks)
Correct x or y coordinate, or method to find midpoint using \frac{3+(-5)}{2} or \frac{-12+10}{2} .
(1)
(-1, \ -1)(1)
2.
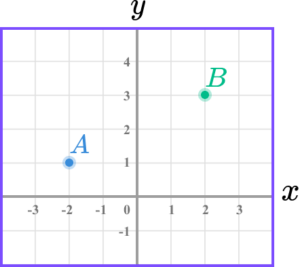
(a) Write down the coordinates of point A.
(b) Find the coordinates of the midpoint AB.
(c) On the grid, mark with a cross the point (-2, \ 3). Label this C.
(3 marks)
(a) (-2, \ 1)
(1)
(b) (0,2)
(1)
(c)
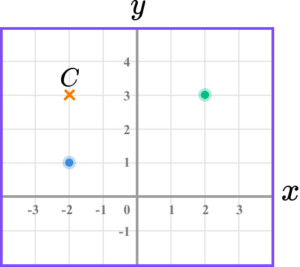
Point marked in correct position.
(1)
3. A line segment joins the points P and Q, and has midpoint M.
P has coordinates (9, \ 5) and M has coordinates (15, \ 8).
The point R is placed such that PQR is a right-angled triangle.
The y coordinate of R is 5. What is the x coordinate of R?
(3 marks)
Method to find the coordinates of the endpoint, such as +6 to x coordinate or +3 to y coordinate.
(1)
Q = (21, \ 11)(1)
x coordinate of R = 21 .
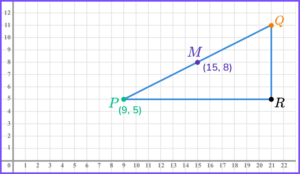
(1)
Learning checklist
You have now learned how to:
- Find the midpoint of a line segment joining two points
- Find a missing endpoint given one endpoint and the midpoint
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.