Negative Numbers

Here we will learn about negative numbers including how to add, subtract, multiply, and divide negative numbers.

There are also negative numbers worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are negative numbers?

Negative numbers are any numbers less than zero and have a negative or minus sign (−) in front of them.

Numbers greater than zero are referred to as positive numbers. If there is no sign in front of a number the number is positive.

On the number line below we can see some positive and negative integers (whole numbers):

The numbers in orange are negative values and the blue numbers are positive values. Zero is neither positive or negative.

Just like you can add, subtract, multiply and divide positive numbers, you can do the same with negative numbers whether they are integers, decimals or fractions.

What are negative numbers?

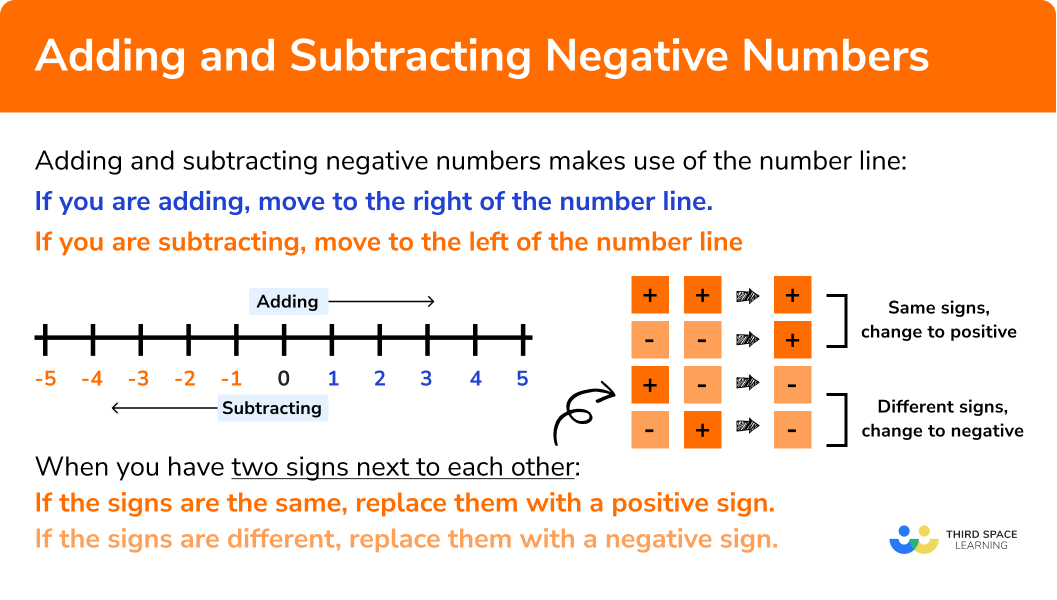
Adding and subtracting negative numbers

When adding and subtracting negative numbers use a number line:

If you are adding, move to the right of the number line.

If you are subtracting, move to the left of the number line.

Sometimes a question might have two operations next to each other:

E.g. 4 + (−2)

If the signs are the same replace with a positive sign.

If the signs are different, replace with a negative sign.

The chart below summarises this:

As a rule of thumb: same signs add, different signs subtract.

Step-by-step guide: Adding and subtracting negative numbers

What do you need to remember when adding and subtracting negative numbers?

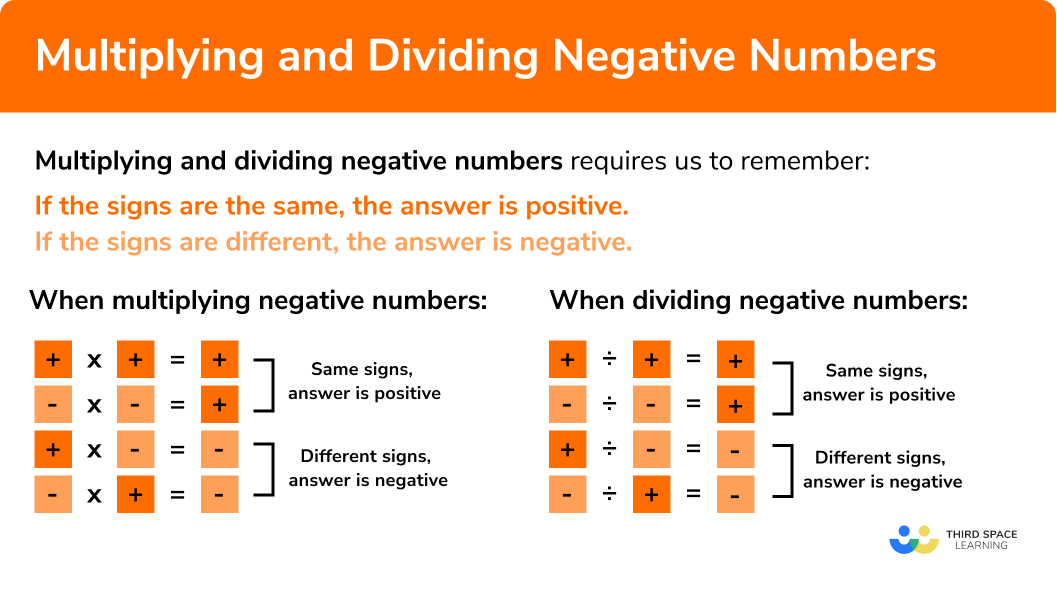
Multiplying and dividing negative numbers

Similar rules apply for multiplying and dividing negative numbers:

If the signs are the same, the answer is positive.

If the signs are different, the answer is negative.

When multiplying negative numbers:

The same rules apply for dividing negative numbers:

Step-by-step guide: Multiplying and dividing negative numbers

What do you need to remember when multiplying and dividing negative numbers?

Negative number arithmetic

There are rules for calculating with negative numbers.

When adding and subtracting numbers it is important to be consistent with positive and negative values. If a number has no sign it means that it is a positive number, for example, 5 is really +5.

When two signs are written next to each other we need to remember these rules

• Two signs that are different become a negative sign
• Two signs that are the same become a positive sign

When we add and subtract negative numbers, we can use a number line to help us understand what direction we need to move. 

E.g.

Work out -2-4

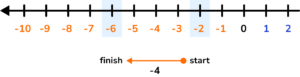
-2-4 = -6

Work out -4+13

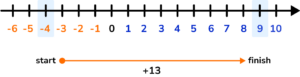
-4+13=9

E.g.

Work out 4+-7

There are two different signs written next to each other. These become negative.

So,  4+-7 = 4-7

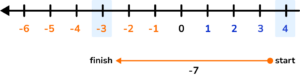
4-7= -3

When multiplying and dividing negative numbers it is often useful to complete the calculation using positive numbers initially. Then, remember the rules

• Multiplying or dividing two numbers with the same sign will give a positive answer
• Multiplying or dividing two numbers with different signs will give a negative answer

E.g.

Work out -4 ×-3

4×3 = 12

Both numbers have the same sign, so the answer will be positive.

-4 ×-3 = 12

E.g.

Work out 12 ÷-2

12÷2=6

The numbers have different signs, so the answer will be negative.

12 ÷-2 = -6

Order integers

Integers (whole numbers) are ordered on a number line based on positive integers and negative integers. The centre of the number line is marked as 0. The integers that are greater than 0 are positive integers. The integers that are less than 0 are negative integers.

The more an integer is negative, the smaller the value is. The more an integer is positive, the bigger the value is.

E.g.

Put these numbers in ascending order.

Remember: ascending means smallest to biggest.

-5 is the most negative number, so this is the smallest value.

4 is the most positive number, so this is the biggest value.

So, putting them in ascending order we get, -5,-3,-2, 0, 1, 2, 3, 4

E.g.

Put these numbers in descending order.

Remember, descending means biggest to smallest.

-1 is the least negative number, so this is the biggest value.

-12 is the most negative number, so this is the smallest value.

So, putting them in descending order we get, -1, -3, -4, -6, -8, -12

How to add and subtract negative numbers

In order to add and subtract negative numbers:

1. If you have two signs next to each other, change them to a single sign.
         If the signs are the same, replace with a positive sign (+).
         If the signs are different, replace with a negative sign (−).
   
2. Circle the first number on the number line.
3. Use the number line to add or subtract your numbers:
        If you are adding, move to the right of the number in step 2 (→).
        If you are subtracting, move to the left of the number in step 2 (←).
4. Write your final answer.

Explain how to add and subtract negative numbers in 4 steps

How to multiply and divide negative numbers

In order to multiply and divide negative numbers:

1. Multiply or divide the numbers normally.
2. Change the sign as necessary using the rules of multiplying and dividing negative numbers:
        If the signs are the same, the answer is positive.
        If the signs are different, the answer is negative.

Explain how to multiply and divide negative numbers in 2 steps

Negative numbers examples

Example 1: adding a positive number

1. If you have two signs next to each other, change them to a single sign.

If the signs are the same in the middle of the calculation, replace with a positive sign (+).

If the signs are different, replace with a negative sign (−).

In this case you do not have two signs next to each other.

2Circle the first number on the number line.

The first number in the question is (−5)

3Use the number line to add or subtract your numbers.

If you are adding, move to the right of the number in step 2 (→).

If you are subtracting, move to the left of the number in step 2 (←).

In this case we are adding the 8 so move 8 spaces right from the (-5) on the number line:

4Write your final answer.

Example 2: subtracting a negative number (two operations)

Circle the first number on the number line.

The first number in the question is (-7)

Use the number line to add or subtract your numbers.

In this case we are adding 5 so move 5 spaces right from the (-7) on the number line:

Example 3: multiplying negative numbers

Example 4: dividing negative numbers

Example 5: mixed operations (Order of operations)

Circle the first number on the number line.

The first number in the question is 3.

Use the number line to add or subtract your numbers and write your final answer.

In this case we are subtracting the 12 so move 12 spaces left from the 3 on the number line:

Final answer:

\[3 – 12 = -9\]

Example 6: real life word problem

The table below shows the temperatures recorded in Leicester at different times of the day.

a) What is the product of the highest and lowest temperatures?

b) What is the difference between the temperatures at 2am and 1pm?

To calculate a):

To calculate b):

Circle the first number on the number line.

The first number in the question is (-8):

Use the number line to add or subtract your numbers:
If you are adding, move to the right of the number in step 2 (→).
If you are subtracting, move to the left of the number in step 2 (←).

In this case we are subtracting the 3 so move 3 spaces right from the (-8) on the number line:

Common misconceptions

• Greater negative does mean a larger number

Students sometimes assume that the larger a negative number the greater it is. For example, students might incorrectly assume -3 is greater than 2 because 3 is a larger number.

• Raising a negative number to a power greater than one

Remember when raising a negative number to a power greater than 1 the resulting answer could be positive or negative. When you raise a negative number to an odd exponent the resulting answer is negative, when you raise a negative number to an even exponent the resulting answer is positive.

• Changing signs when adding and subtracting
  When adding or subtracting with negative numbers the signs change only if they are next to each other in the middle of the calculation and are different

The next lessons are

• Factors, multiples and primes
• Fractions
• Decimals

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.