4. Which is an incorrect factor tree for $ 144 $?

Factors, multiples and primes

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Arithmetic

This topic is relevant for:

GCSE Maths Number

Factors, Multiples And Primes

Here we will learn about factors and multiples and primes, including what they are and how they can be used.

There are also factors, multiples and primes worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are factors, multiples and primes?

Factors, multiples and primes are different types of numbers.

A factor is a number which divides into another number exactly with no remainders.

For example,

What are the factors of $12$ ?

To do this we can think of pairs of numbers which multiply together to make $12$ .

\begin{aligned} &1\times 12 \\\\ &2\times 6 \\\\ &3\times 4 \end{aligned}

So the factors of $12$ are: $1, 2, 3, 4, 6$ and $12.$

Step-by-step guide: Factors

A multiple of a number is a number in its times table.

For example,

The multiples of $4$ are: $4, 8, 12, 16, 20$ and so on.

Step-by-step guide: Multiples

See also: Factors and multiples

A prime number is a number that only has two factors, $1$ and itself.

The first few prime numbers are: $2, 3, 5, 7, 11, 13, 17, 19, 23$ and so on.

Step-by-step guide: Prime numbers

What are factors, multiples and primes?

How to use factors, multiples and primes

We can use factors, multiples and primes to work with:

Prime factors
Factor trees
Lowest common multiple (LCM)
Highest common factor (HCF)

How to use factors, multiples and primes?

Prime factors

Prime factors are factors of a number that are also prime numbers. We can write any number as a product of its prime factors – this is called prime factorisation (prime factorization).

For example,

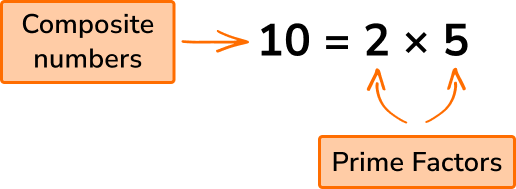
Factors, Multiples and Primes HUB image 1

A composite number is a non-prime number which is the product of two or more prime factors. All of these types of numbers are integers (whole numbers).

Step-by-step guide: Prime factors

Factor trees

Factor trees are a way of finding the prime factors of a number. This is useful when asked to write a number as a product of its prime factors.

For example,

A factor tree for $150$ may look like this,

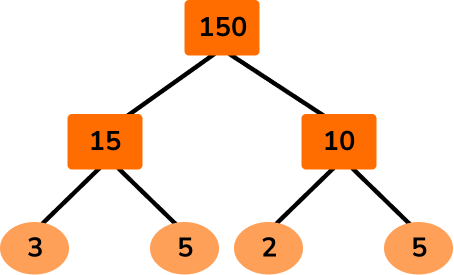
Factors, Multiples and Primes HUB image 2

Each branch in the tree is split into two factors which multiply together to make the number they are branching from. Once the factor at the end of the branch is a prime number, its only two factors are itself and one so the branch stops and we circle the number.

Here is $150$ as a product of its prime factors,

$150=3\times 5\times 2\times 5=2\times 3\times 5^2$ .

Step-to-step guide: Factor trees

Lowest common multiple

The lowest common multiple (LCM) or least common multiple is the smallest integer that belongs to the multiplication table of two or more numbers – it is the lowest value that is a multiple of each number.

For example,

Find the LCM of $4$ and $5$ .

Let’s start by writing the multiples of $4$ and $5$ .

Multiples of $4: \quad \quad 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, …$

Multiples of $5: \quad \quad 5, 10, 15, 20, 25, 30, 35, 40, 45, ...$

We can see that the smallest positive integer that occurs in each list is $20$ , so the lowest common multiple of $4$ and $5$ is $\bf{20.}$

Note: $40$ occurs in both lists so is a common multiple, but not the lowest common multiple.

Step-to-step guide: Lowest common multiples

Highest common factor

The highest common factor (HCF) or greatest common factor is the largest integer that two or more numbers can be divided by – it is the highest value that is a factor of each number.

For example,

Find the HCF of $12$ and $20$ .

Let’s start by writing the factors of $12$ and $20$ .

Factors of $12: \quad \quad 1, 2, 3, 4, 6, 12$

Factors of $20: \quad \quad 1, 2, 4, 5, 10, 20$

We can see the highest number that occurs in each list is $4,$ hence the highest common factor of $12$ and $20$ is $4.$

Note: $1$ and $2$ occur in both lists, so they are common factors, but not the highest common factor.

Step-to-step guide: Highest common factor

See also: HCF and LCM

Factors and multiples worksheet

Get your free factors and multiples worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE!

Factors and multiples worksheet

Get your free factors and multiples worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE!

Factors and multiples examples

Example 1: listing factors

List the factors of $18$ .

Use factor pairs, starting from $1,$ then $2$ and so on.

\begin{aligned} 18&= 1\times 18\\\\ &=2\times 9\\\\ &=3\times 6 \end{aligned}

The factors of $18$ are: $1, 2, 3, 6, 9$ and $18$ .

Example 2: listing multiples

Write down the first $6$ multiples of $7$ .

Think about the $7$ times tables.

\begin{aligned} &1\times 7=7 \\\\ &2\times 7=14 \\\\ &3\times 7=21 \\\\ &4\times 7=28 \\\\ &5\times 7=35 \\\\ &6\times 7=42 \end{aligned}

The first $6$ multiples of $7$ are: $7, 14, 21, 28, 35$ and $42$ .

Example 3: prime factors

Write $42$ as a product of its prime factors.

There are several ways to do this.

One way is to divide the number by prime numbers and continue to do so until the final answer is a prime number.

First divide by $2$ ,

$42\div 2 = 21$ .

Then divide by $3$ ,

$21\div 3=7$ .

$7$ is prime so we can stop.

So,

$42=2\times 3\times 7$

$\begin{aligned} 42&= 2\times 21\\\\ &=2\times 3\times 7 \end{aligned}$

$42$ as a product of its prime factors is $2 \times 3 \times 7$ .

Example 4: factor trees

Construct a factor tree for $180$ .

First think of a pair of numbers that multiply together to make $180$ .

180=18\times 10

Then continue to construct branches from the $18$ and the $10.$ Continue until each branch ends with a prime number.

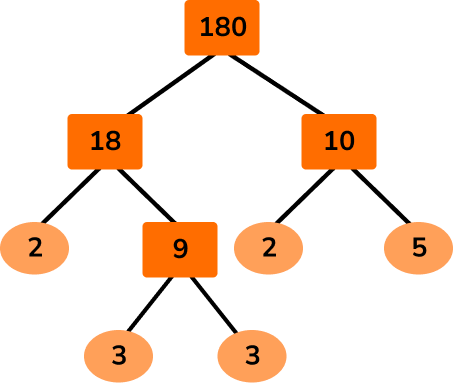
Factors, Multiples and Primes HUB image 3

We can write $180$ as a product of its prime factors,

$180=2\times 3\times 3\times 2\times 5$ .

Or in numerical order,

$180=2\times 2\times 3\times 3\times 5$ .

Or in index form,

$180=2^2\times 3^2\times 5$ .

Note: Most numbers have many possible factor trees.

Example 5: lowest common multiple

Find the lowest common multiple of $12$ and $20$ .

We can list some multiples of $12$ and $20$ and find the LCM.

Multiples of $12$ are: $\quad 12, 24, 36, 48, 60, 72 …$

Multiples of $20$ are: $\quad 20, 40, 60, 80 …$

The LCM of 12 and 20 is 60.

Alternatively you can use prime factorisation and Venn diagrams.

Write the numbers as products of their prime factors.

$\begin{aligned} &12=2\times 2\times 3 \\\\ &20=2\times 2\times 5 \end{aligned}$

Put the prime factors into a Venn diagram.

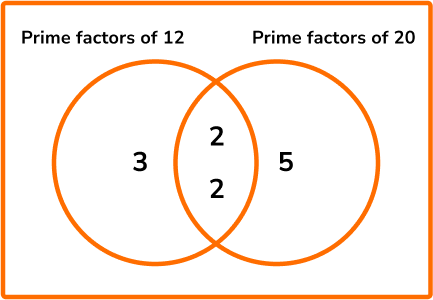
Factors, Multiples and Primes HUB image 4

Multiply each prime factor in the Venn diagram to find the LCM.

$3\times 2\times 2\times 5=60$

The LCM of $12$ and $20$ is $60.$

Example 6: highest common factor

Find the highest common factor of $30$ and $48$ .

We can list the factors of $30$ and $48$ , using factor pairs to help.

\begin{aligned} 30&= 1\times 30\\\\ &=2\times 15\\\\ &=3\times 10\\\\ &=5\times 6 \end{aligned}

$\begin{aligned} 48&= 1\times 48\\\\ &=2\times 24\\\\ &=3\times 16\\\\ &=4\times 12\\\\ &=6\times 8 \end{aligned}$

The factors of $30$ are: $\quad \quad 1, 2, 3, 5, 6, 10, 15$ and $30$

The factors of $48$ are: $\quad \quad 1, 2, 3, 4, 6, 8, 12, 16, 24$ and $48$

The HCF of $30$ and $48$ is $6.$

Alternatively you can use prime factorisation and Venn diagrams.

Write the numbers as products of their prime factors.

$30=2\times 3\times 5$

$48=2\times 2\times 2\times 2\times 3$

Put the prime factors into a Venn diagram.

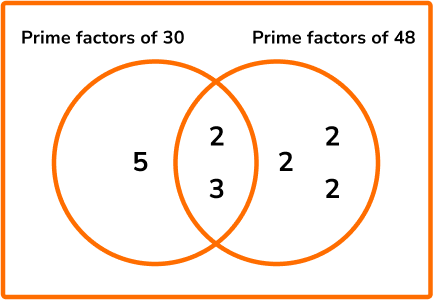
Factors, Multiples and Primes HUB image 5

Multiply the prime factors in the intersection to find the HCF.

$2\times 3=6$

The HCF of $30$ and $48$ is $6.$

Common misconceptions

$1$ and prime numbers

$1$ is not a prime number. This is because it only has one factor, rather than the $2$ factors needed to be a prime number.

Factors and multiples

Factors and multiples are easily mixed up. Remember multiples are the multiplication table, whereas factors are the numbers that go into another number without a remainder.

Remember the number itself for factors and multiples

All numbers are a factor of themselves and a multiple of themselves.

For example,

Think of the number $6.$

The factors of $6$ are: $1, 2, 3, 6.$

The multiples of $6$ are: $6, 12, 18, 24$ and so on.

So $6$ is a factor and a multiple of itself.

Practice factors and multiples questions

50, 100, 150, 200, 250 \dots

$1, 2, 5, 10, 25,$ and $50$

$2, 5, 10$ and $25$

2\times 5^2

To list the factors of 50 we can use factor pairs.

\begin{aligned} 50&= 1\times 50\\\\ &=2\times 25\\\\ &=5\times 10 \end{aligned}

So the factors of $50$ are $1, 2, 5, 10, 25$ and $50.$

$1, 3, 5$ and $15$

1+2+3+4+5

3\times 5

$15, 30, 45$ and $60$

We need the first $4$ numbers of the $15$ times table.

\begin{aligned} &1\times 15=15\\\\ &2\times 15=30\\\\ &3\times 15=45\\\\ &4\times 15=60 \end{aligned}

So, the first $4$ multiples of $15$ are: $15, 30, 45$ and $60.$

2,2,2,3,5

2^3 \times 3\times 5

2\times 3\times 5

12\times 10

Divide $120$ by $2$ and other primes until you are left with a prime number.

\begin{aligned} 120&= 2\times 60\\\\ &=2\times 2\times 30\\\\ &=2\times 2\times 2\times 15\\\\ &=2\times 2\times 2\times 3\times 5 \end{aligned}

We can then write the product of prime factors in index form,

$120=2^3 \times 3\times 5$ .

Factors, Multiples and Primes HUB practice question 4 image 1

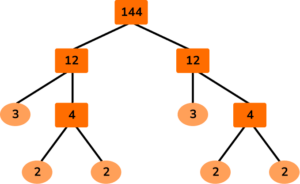
Factors, Multiples and Primes HUB practice question 4 image 2

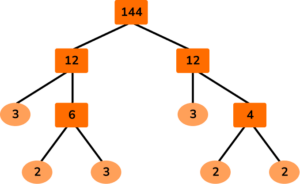
Factors, Multiples and Primes HUB practice question 4 image 3

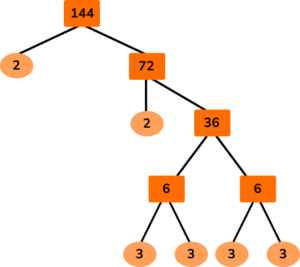
Factors, Multiples and Primes HUB practice question 4 image 4

The branches from a number need to multiply together to make that number.

$3 \times 3$ ≠ $6$

Also, the prime numbers should all multiply together to make 144.

For option D,

$2\times 2\times 3\times 3\times 3\times 3=324$ .

20

2

40

80

Write down the multiples of 8 and the multiples of 10 and see which is the lowest number that occurs in both lists.

Multiples of $8: \quad 8, 16, 24, 32, 40, 48, …$

Multiples of $10: \;\; 10, 20, 30, 40, 50, …$

So, $40$ is the LCM of $8$ and $10.$

Alternatively you can use prime factorisation and Venn diagrams.

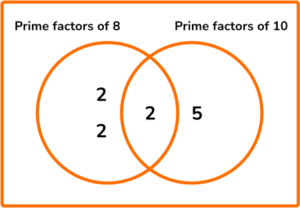
\text{LCM}=2\times 2\times 2\times 5=40

7

28

21

14

List the factors of $56$ and $50$ and see which is the highest number in both lists.

Factors of $56$ are: $\quad 1, 2, 4, 7, 8, 14, 28$ and $56$

Factors of $70$ are: $\quad 1, 2, 7, 10, 14, 35$ and $70$

So, $14$ is the HCF of $56$ and $70$ .

Alternatively you can use prime factorisation and Venn diagrams.

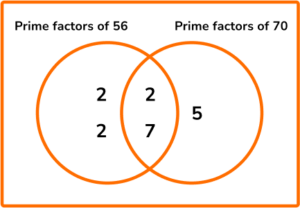
The HCF is the product of the prime factors in the intersection.

\text{HCF}=2\times 7=14

Factors and multiples GCSE questions

1. (a) Write down a multiple of $7$ between $20$ and $30$ .

(b) Write down two factors of $70$ that are prime numbers.

(3 marks)

Show answer

(a)

$21$ or $28$

(1)

(b)
One answer from $2, 5, 7$ .

(1)

Another one from $2, 5, 7$ .

(1)

2. (a) Find the highest common factor of $22$ and $77$ .

(b) Find the lowest common multiple of $22$ and $77$ .

(4 marks)

Show answer

(a)

Factors of $22: 1, 2, 11$ and $22$

Factors of $77: 1, 7, 11,$ and $77$

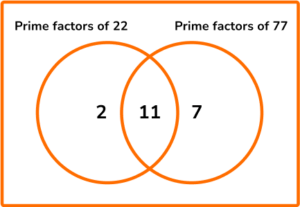
Factors, Multiples and Primes HUB GCSE question 2a

(1)

HCF = 11

(1)

(b)

Multiples of $22: 22, 44, 88, 110, 132, 154, \dots$

Multiples of $77$ are: $77, 154, 231, \dots$

\text{LCM}=2\times11\times7

(1)

LCM = 154

(1)

3. Two buses leave the depot at $9 \; am.$

Bus B takes $55$ minutes to complete its journey and return to the depot.

What time is it when both buses are back at the depot together?

(4 marks)

Show answer

\begin{aligned} &45=3\times 3\times 5 \\\\ &55=5\times 11 \end{aligned}

(1)

\text{LCM}=3\times3\times5\times11=495

(1)

495=8.25 \ \text{hours}

(1)

$17$ : $15$ or $5$ : $15 \ \text{pm}$

(1)

Learning checklist

You have now learned how to:

Find factors and multiples

Write numbers as a product of their prime factors

Find the lowest common multiple

Find the highest common factor

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.